基于核空间的模糊聚类方法在储层预测中的应用

印兴耀，叶端南，张广智

(中国石油大学地球科学与技术学院，山东青岛 266555)

基于核空间的模糊聚类方法在储层预测中的应用

印兴耀，叶端南，张广智

(中国石油大学地球科学与技术学院，山东青岛 266555)

基于核空间的模糊C均值聚类方法是一种模式识别的新方法。在地震属性聚类处理时常常会遇到非超球体数据以及非线性类间边界等问题，而传统的模糊C均值聚类方法无法行之有效地解决。将核空间方法引入传统的模糊C均值聚类方法中，并应用于储层预测。针对地震属性聚类问题中不同属性对于储层的敏感性不同，将特征权重和模糊指数等参数加以优化，提高新的模糊聚类方法的储层预测效果。对实际资料的计算与分析结果表明，新的基于核空间的模糊C均值聚类方法可以更准确地刻画碳酸盐岩含气储层边界。

核空间;模糊聚类;地震属性;储层预测

常规的地震资料分析方法大多利用地震资料的振幅信息，而地震属性［1］分析技术可以更全面地利用地震数据中其他方法无法提取的信息。地震属性分析技术不仅扩展了地球物理技术在实际生产中的应用范围，而且对于储层预测技术的发展也有着积极的推动作用。当前，地震单属性解释技术已经无法满足储层预测技术发展的需要，多属性综合解释已成为地震勘探资料解释的主要发展方向。近年来，随着地震属性分析技术在地震资料解释中日渐广泛的应用，已经形成了一整套包括地震属性提取技术、地震属性优化技术、地震属性聚类技术以及地震属性转换技术等在内的综合地震属性分析技术［2-5］。同时，有许多模式识别和人工智能中比较有效的方法被引入地球物理解释当中，其中基于模糊划分的模糊C均值聚类分析方法(FCM)已在对于隐蔽油气藏的预测当中取得了一定的效果［4］。笔者将基于核空间的模糊C均值聚类分析方法(KFCM)应用于地震属性聚类分析，并用该方法进行储层预测。

1 方法概述

1.1 地震属性聚类分析

地震属性是指由叠前或叠后地震数据，通过数学变换而导出的有关地震波的几何形态、运动学特征、动力学特征和统计学特征参数［6］。地震属性分析技术就是指通过对地震属性的分析，研究地层中的岩石性质和流体性质等，并揭示不同区域的岩石性质和流体性质之间的相对关系。通过模糊聚类技术，仅仅依靠地震数据，就可将目标区域的各种相带进行划分。

1.2 模糊C均值聚类方法

模糊C均值聚类方法(fuzzy C-means，FCM)是基于目标函数的聚类算法中理论最为完善、应用最广泛的一种。早在1973年Bezdek就提出了模糊C均值聚类算法，作为早期硬C均值聚类的一种改进［7-8］。

假设对于给定的数据集X={x1，x2，…，xn}，FCM将这n个向量划分为p个模糊组，这里的p也就是所期望的聚类数目。FCM使用模糊划分，对每个给定的点用隶属度u(0≤u≤1)来确定其属于各个组的程度。FCM的目标函数如下:

式中，U为隶属度u组成的隶属度矩阵;C={c1，c2，…，cp}为各个模糊组的聚类中心;第k个数据点与第i个聚类中心之间的欧几里得距离;m∈［1，∞)是一个加权指数，又称作平滑参数。当m=1时，模糊C均值聚类即转化为硬C均值聚类。 聚类的准则为取J(U，C)的极小值min{J(U，C)}。

由于矩阵U中不同数据点的隶属度u是相互独立的，因此上述极值的约束条件为

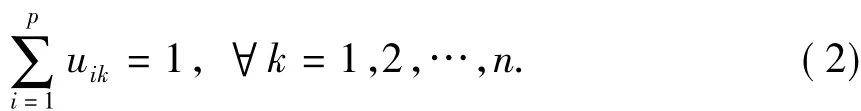
构造如下新的目标函数:

其中，λk(k=1，2，…，n)是式(2)的n个约束的拉格朗日乘子。易推导出使式(1)达到极小值的必要条件为

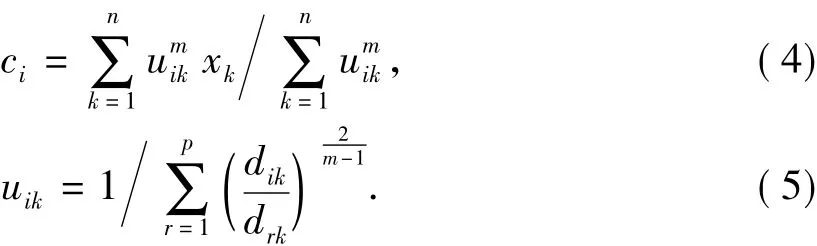
1.3 基于核空间的模糊C均值聚类方法

由于传统的FCM算法本质上的缺陷，使得传统的FCM算法不能对非超球体数据、被噪声污染的数据、多种模式原型混合的数据以及不对称数据等多种数据结构进行聚类，而这些正是地震属性分析所需要面对的问题。大量学者对FCM算法进行了优化和改进［9-11］。

基于核空间的模糊C均值聚类算法(KFCM)的基本思想是:通过不同的核函数将数据映射到高维特征空间，使得在线性空间没有显现的特征凸现出来，扩大特征间的差异，再在高维度的特征空间中进行聚类。

由前文假设条件以及式(1)，可得到KFCM的目标函数为

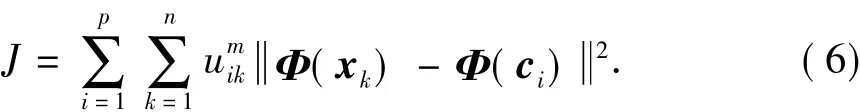
式中，Φ(xk)，k=1，2，…，n为给定的数据集 X= {x1，x2，…，xn}在相应核空间中的象;Φ(ci)，i=1，2，…，p为各个聚类中心C={c1，c2，…，cp}在相应核空间中的象。

其中，K(·)即为相应的核函数。式(7)即为选用核函数K(·)时，在特征空间内xk与ci之间的欧几里得距离。

在特征空间内隶属度函数和聚类中心分别为

将核方法与FCM方法结合后，对于聚类时类与类之间的非线性边界处理能力大为改善。经过对多种核函数(线性核函数、多项式核函数、高斯核函数、Sigmoid核函数)进行试算发现，高斯核函数和Sigmoid核函数的效果要优于线性核函数和多项式核函数。Sigmoid核函数对于不同的数据表现的效果并不稳定，而高斯核函数则表现不错，对于不同的数据它的泛化性和收敛域都比较理想。因此，采用高斯核函数。

为了区分不同地震属性对于聚类分析结果的不同影响，同时为了降低数据中离群点对算法的干扰，给每个属性设置了加权系数。在权值的设定上采用的是复相关系数的倒数赋权法，即对于每一个属性xk，用其余属性对于xk的相关程度的倒数来确定属性xk在整个样本集中的权重。

本文中所选用的KFCM算法流程如下:

(1)根据需要，对各项计算参数进行初始化，并由已知的属性数据集，计算出各个属性的权值wk，k =1，2，…，n;

(2)生成初始的隶属度矩阵U和聚类中心C={c1，c2，…，cp};

(3)由式(9)计算出聚类中心在特征空间中的象Φ(ci)，i=1，2，…，p;

(4)计算目标函数，若满足初始设定的条件或已达到最大迭代次数，则算法停止;

(5)根据式(10)计算新的隶属度矩阵，返回步骤(3)。

1.4 计算参数的优选方法

在地震属性分析中，基本的相带划分已经实现，对于相带边界的精确标识以及线性空间中无法识别出特征信息的相带，也可以通过基于核空间的聚类方法予以解决。但是，用作参考的地震属性组合中会含有冗余的信息，对聚类结果以及计算速度造成或多或少的影响。同时，在不同的地区，具体的地质情况是不同的，原本在某一地区应用效果比较理想的属性，到了另一地区很可能就不适用了。解决这个问题，除了用专家选择的方法［2］外，本文中用复相关系数倒数赋权法对各个参与计算的属性进行权值分配以优化模糊聚类的效果。

复相关系数倒数赋权法是在方差倒数赋权法的基础上提出的。每一个属性的复相关系数反映了该属性被其他属性代替的可能。该方法权重表达式为

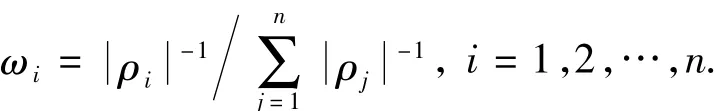
式中，ρ为复相关系数;ω为该属性的权值，也就是复相关系数倒数的绝对值。

另外，模糊聚类方法在应用于地震勘探领域的过程中，比较难确定的计算参数还有聚类的模糊加权指数m和最优的聚类数。因为地震资料中所携带的不仅仅是岩石的信息，还会包含岩石中所含流体的信息，从而导致地震相带的分类并不完全与沉积相带一致。

高新波等［12］提出了一种基于模糊决策理论选取最优模糊加权指数m的方法。一个好的聚类结果应当是类内加权均方误差小，而且类间可分性好。该方法中定义，确定最佳加权指数m*的这一决策问题的模糊目标G为极小化模糊聚类目标函数J(U，C)，模糊约束C为极小化模糊聚类划分熵H(U，C)。模糊聚类划分熵的表达式为

其中，底数a∈(1，+∞)，且约定当uik=0时，有uiklogauik=0。由模糊聚类有效性可知，最佳的分类应满足mΩin {Hm［U，C］}。其中，Ω为模糊聚类参数，在FCM算法中有Ω={m，U，C}。也就是说，好的聚类结果应当是划分成合适的种类数，并且类间具有较好分离度，此时的分类结果对应于较大的分类确定性和较小的模糊性。

2 实例分析

2.1 试验数据试算

选用检验聚类算法有效性指标性能的UCI数据库中的Iris数据集。该数据集包含4种属性，共150组数据样本。根据这4种属性，Iris数据集中的样本被分为3类(setosa类、versicolor类和virginica类)，每类含50组数据。依据样本的4种属性，setosa类可以比较容易地与其他2类分开，但是versicolor类与virginica类在这4种属性两两交会的情况下，都很难划分出明显的界限。这说明setosa类与其他2类存在着明显的线性差异，通过简单的线性交会图就可以进行区分，而versicolor类和virginica类之间的差异是非线性的，在线性空间内很难进行区分，需要构造更高维度的空间才可以将二者区别开来。对Iris数据使用传统的FCM方法和本文中KFCM方法进行聚类，以验证KFCM方法对于存在非线性特征差异的类进行划分的能力。其中，两种方法所用计算参数相同，模糊加权指数m=1.5，分类数为3。计算结果的正确率对比见表1。

表1 FCM与KFCM对Iris数据的分类正确率Table 1 Accuracy of FCMmethod and KFCMmethod %

由表1可见:对于在线性空间内易分类的setosa类，FCM与KFCM的分类正确率都很高，没有分类错误的样本;对于在线性空间内不易区分的versicolor类和virginica类，FCM方法的正确率明显低于KFCM方法。以上是经过200次计算得到的数据统计平均的结果，这验证了KFCM方法在处理类间非线性边界时的优越性。同时由于核函数的优化，在分类时不必通过反复迭代等大量的计算在线性空间内寻找类间的差异，从而使得KFCM方法在计算效率上也要高于传统的FCM方法。大量的试验发现，在Iris样本数据的处理过程中二者的差别并不是很悬殊，FCM方法和KFCM方法最少迭代次数分别为39、37，最多迭代次数分别为54、45。可能是由于数据集只含有150个样本，数据量较小导致两种方法的迭代次数差别不大，但KFCM方法在整体上仍优于传统的FCM方法。

2.2 实际数据试算

为了进一步验证KFCM方法对于实际地震资料的处理能力，采用上述2种方法对沿层地震属性进行分析，得到同一地质层位中不同相带的分布情况。选用某地区的7种沿层地震属性(图1)作为样本属性特征［15］来进行试算，这7种属性分别是:弧长属性(图1(a))、平均瞬时频率属性(图1(b))、平均瞬时相位属性(图1(c))、能量半时属性(图1 (d))、振幅峰度属性(图1(e))、瞬时频率斜率属性(图1(f))、反射强度斜率属性(图1(g))。所有属性在进行计算前都经过归一化处理。

该地区为海相碳酸盐岩储层，目标地层主要相带为丘状礁滩体和前积体，生物礁、滩交错分布。通过沉积相平面分布图(图2)可以大致了解该地区的相带分布情况。其中黑色箭头所指的狭长区域为生物礁相，其余4个相带分别为:台地边缘相、台地前缘斜坡相、陆棚相、深海陆棚相。其中生物礁相(箭头所指区域)已有探井证实为含气储层。通过对单属性的观察可以看出主要相带的条带状分布趋势。但是，不同相带之间的界限不明显，局部细节的刻画不明确，而且作为储层的目标区域也无法与周围的非储层相带加以区分。

使用传统的FCM和本文中KFCM方法分别对归一化后的地震属性集进行聚类分析。其中，两种方法采用相同的计算参数，模糊加权指数m=1.38，最佳分类数p=5.4，KFCM方法采用高斯核函数，聚类分析结果如图3所示。

由图3可以看出，KFCM方法在分类的精确程度上要优于传统的FCM方法。利用核技术可以将地震属性与地质信息之间的非线性关系正确地反映出来，在不同分类之间的边界以及局部细节的刻画方面，KFCM方法的正确率都明显高于传统的FCM方法。特别是图3(b)中箭头处所示的生物礁链储层，在图3(a)中完全无法正确显示。

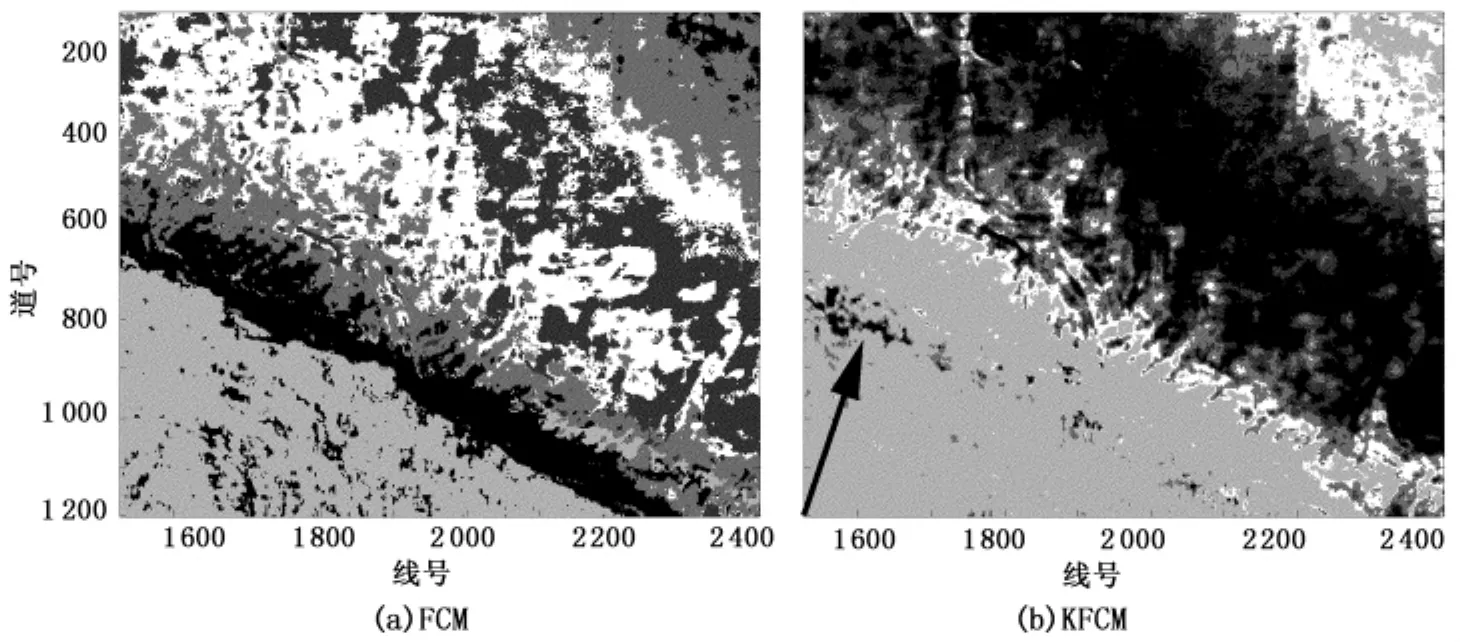
图3 聚类数为5时FCM和KFCM聚类结果对比Fig.3 Comparison result of FCMand KFCMfor 5 clusters

由于求取的最佳分类数为5.4次，又进行了一次聚类数为6的试验，再次对KFCM方法进行验证以期获得稳定的结果(图4)。图4再次证实了KFCM方法对地质信息与地震属性之间的非线性关系的反映能力比传统的FCM方法要好，并且具有较强的对类间边界的描述能力。

在实际资料的处理过程中，对传统的FCM方法和KFCM方法的迭代次数进行了统计。FCM和KFCM的最少迭代次数分别为128和36，最多迭代次数分别为437和74。实际资料中共有809301个样本，可以看出在样本空间较大的情况下，KFCM方法在计算效率上要远远优于传统的FCM方法。因为核函数的作用，可以在高维空间处理一些线性问题，因此KFCM方法相对于FCM方法不仅仅是分类精度上有所提高，在计算效率上也有很显著的提高，迭代次数要少很多。

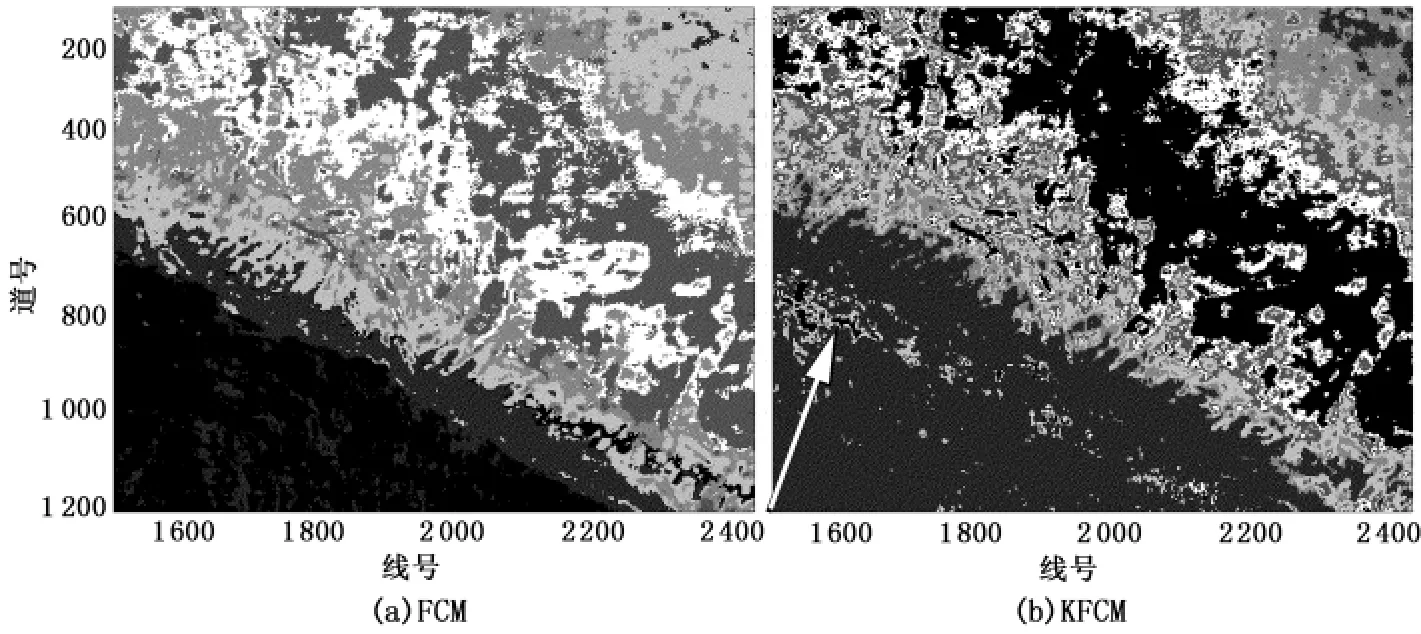
图4 聚类数为6时FCM和KFCM聚类结果对比Fig.4 Comparison result of FCMand KFCMfor 6 clusters

3 结束语

基于核空间的模糊C均值聚类方法是一种利用核函数进行模糊聚类的新方法，它的适用性很强，可以处理多种类型的数据。对于一些传统FCM方法无法解决的数据分类问题，比如超球体数据、被噪声污染的数据、多种模式原型混合的数据以及不对称数据等多种数据结构的分类问题，KFCM方法能够比较好地解决。同时对于聚类问题中的非线性问题，传统的FCM方法无法解决，但是KFCM方法就可以很好地完成。

在地震属性聚类分析中，常常会遇到的一些困难，比如类间非线性边界难处理、地震属性的非线性特征差异难以得到体现、离群点对聚类结果影响大等问题，这些问题都可以通过KFCM方法加以解决。相对于传统FCM方法的聚类结果，使用KFCM方法进行聚类，无论是聚类结果的正确性还是局部细节刻画的精度都有很大提高，并且通过结合各种计算参数的优选方法，使得KFCM方法的效果更为理想。在进行地球物理勘探的过程中，尤其是在目标地区缺少井资料等先验信息的情况下，KFCM方法可以成为一种强有力的储层预测手段。

［1］QUINCY Chen，STEVE Sidney.Seismic attribute technology for reservoir forecasting and monitoring［J］.The Leading Edge，1997，16(5):445-456.

［2］印兴耀，周静毅.地震属性优化方法综述［J］.石油地球物理勘探，2005，40(4):482-489.

YINXing-yao，ZHOU Jing-yi.Summary of optimum methods of seismic attributes［J］.Oil Geophysical Prospecting，2005，40(4):482-489.

［3］印兴耀，孔国英，张广智.基于核主成分分析的地震属性优化方法及应用［J］.石油地球物理勘探，2008，43(2):179-183.

YINXing-yao，KONG Guo-ying，ZHANG Guang-zhi.Seismic attributes optimization based on kernel principal component analysis(KPCA)and application［J］.Oil Geophysical Prospecting，2008，43(2):179-183.

［4］杨培杰，印兴耀，张广智.模糊C均值地震属性聚类分析［J］.石油地球物理勘探，2007，42(3):322-324，347.

YANG Pei-jie，YINXing-yao，ZHANG Guang-zhi.Cluster analysis of seismic attributes by fuzzy C-mean algorithm［J］.Oil Geophysical Prospecting，2007，42(3): 322-324，347.

［5］叶端南，印兴耀，张广智.地震属性转换中褶积算子的应用研究［C］//中国地球物理协会.中国地球物理年会论文集.合肥:中国科学技术大学出版社，2009: 150.

［6］何碧竹，周杰，汪功怀.利用多元地震属性预测储层信息［J］.石油地球物理勘探，2003，38(3):258-262.

HE Bi-zhu，ZHOU Jie，WANG Gong-huai.Using multivariate seismic attributions to predict reservoir information［J］.Oil Geophysical Prospecting，2003，38(3):258-262.

［7］BEZDEK JC.Pattern recognition with fuzzy objective function algorithms［M］.New York:Plenum Press，1981.

［8］HATHAWAY RJ，BEZDEK JC，TUCKERW T.Convergence results for the fuzzy c-means clustering:counter examples and repairs［J］.IEEE Trans PAMI，1987，17 (5):873-877.

［9］伍忠东，高新波，谢维信.基于核方法的模糊聚类算法［J］.西安电子科技大学学报:自然科学版，2004，31(4):533-537.

WU Zhong-dong，GAO Xin-bo，XIE Wei-xin.A study of a new fuzzy clustering algorithm based on the kernel method［J］.Journal of Xidian University，2004，31(4): 533-537.

［10］孔攀，邓辉文，江欢，等.改进的基于核函数的模糊聚类算法［J］.计算机应用，2008，28(9):2338-2340.

KONG Pan，DENG Hui-wen，JIANG Huan，et al.Improved kernel-based fuzzy clustering algorithm［J］.Journal of Computer Applications，2008，28(9):2338-2340.

［11］普运伟，金炜东，朱明，等.核模糊C均值算法的聚类有效性研究［J］.计算机科学，2007，34(2):207-210，229.

PU Yun-wei，JINWei-dong，ZHU Ming，et al.On cluster validity for kernelized fuzzy C-mean algorithm［J］.Computer Science，2007，34(2):207-210，229.

［12］高新波，裴继红，谢维信.模糊C-均值聚类算法中加权指数m的研究［J］.电子学报，2000，28(4):80-83.

GAO Xin-bo，PEI Ji-hong，XIE Wei-xin.A study of weighting exponentmin a fuzzy C-means algorithm［J］.Acta electronica Sinica，2000，28(4):80-83.

［13］宫改云，高新波，伍忠东.FCM聚类算法中模糊加权指数m的优选方法［J］.模糊系统与数学，2005，19(1):143-148.

GONG Gai-yun，GAO Xin-bo，WU Zhong-dong.An optimal choice method of parametermin FCMclustering algorithm［J］.Fuzzy Systems and Mathematics，2005，19(1):143-148.

［14］肖满生，阳娣兰，张居武，等.基于模糊相关度的模糊C均值聚类加权指数研究［J］.计算机应用，2010，30(12):3388-3390.

XIAO Man-sheng，YANG Di-lan，ZHANG Ju-wu，et al.Research of weighting exponent of fuzzy C-means algorithm based on fuzzy relevance［J］.Journal of Computer Applications，2010，30(12):3388-3390.

［15］曹辉.地震参数解释的模式识别法［J］.石油地球物理勘探，1994，29(2):140-146.

CAO Hui.A pattern recognition method for seismic parameter interpretation［J］.Oil Geophysical Prospecting，1994，29(2):140-146.

Application of kernel fuzzy C-means method to reservoir prediction

YINXing-yao，YE Duan-nan，ZHANG Guang-zhi

(College of Geosciences in China University of Petroleum，Qingdao266555，China)

The kernel fuzzy C-means(FCM)method is a novel method for pattern recognition.The problems such as nonhyperspherical data and non-linear inter-class boundary are prevalent during seismic attributes clustering process，which could not be resolved effectively by traditional FCMmethod.The kernel function was introduced into traditional FCMmethod for these problems in reservoir prediction.The parameters including feature weights and fuzzy coefficient were optimized for different sensibility of seismic attributes，which could improve the effectiveness of this new kernel FCMmethod for reservoir prediction.The results of experiments on the artificial and real data show that the new kernel FCMmethod can describe the boundaries of gas-bearing carbonate reservoir more accurately.

kernel space;fuzzy clustering;seismic attributes;reservoir prediction

P 631.49

A

10.3969/j.issn.1673-5005.2012.01.009

1673-5005(2012)01-0053-07

2011－10－27

国家油气重大专项课题(2011ZX05014－001－010HZ);中国石油科技创新基金项目(2011D－5006－0301);中国石油大学(华东)自主创新科研计划项目(11CX05006A)

印兴耀(1962－)，男(汉族)，浙江奉化人，教授，博士，博士生导师，从事地球物理勘探方面的教学与研究工作。

(编辑 修荣荣)