基于小波分解的PCNN遥感图像融合算法

符 强，任风华，蒋昌茂，纪元法，赵岭忠

（1.桂林电子科技大学 信息与通信工程学院，广西 桂林 541004；2.桂林师范高等专科学校，广西 桂林 541002）

遥感图像（包括航空摄影像片和航天遥感图像）以特定的空间分辨率和波谱段，如实地、无遗漏地记录地面上的一切客体和地面以下的部分地理信息.无论是全色图像、多光谱图像、红外图像或全息图像，都是地面的综合图像.高空间分辨率全色图像反映了空间结构信息，能够详尽地表达地物的细节特征；低空间分辨率多光谱图像的光谱信息丰富，有利于对地物的识别与解释.将全色图像和多光谱图像进行融合，尽量增强多光谱图像的空间分辨率，可以改善后续处理效果，在土地利用调查、城区识别和森林资源调查等遥感应用领域中有着极其重要的作用［1－2］.

目前关于多光谱图像与高分辨率图像的融合方法主要有IHS变换方法、主成分分析法（PCA）、缨帽变换法（BT）、基于张量积离散小波变换（DWT）的融合方法及基于ARSIS概念的融合方法等.在这些方法中，使用最广泛的是IHS变换方法和小波变换方法.IHS变换方法和小波变换方法都有其不足：IHS变换方法能得到高空间分辨率的图像，但融合结果图像的光谱信息损失严重；采用离散小波变换方法所得融合结果图像有好的光谱信息，但其空间分辨率低，且由于对图像进行分解和重构时进行了抽样，使得融合结果图像中有方块效应［3－5］.

基于上述不足，本文提出了一种新的图像融合方法，即将小波变换和符合生物视觉特性的脉冲耦合神经网络（PCNN）相结合进行遥感图像的融合方法.为了不损失光谱信息，在小波基的选择上进行了对比，并选取了图像保光谱性的DB1作为小波基；同时，为保证融合后图像具有详尽的空间结构信息和丰富的光谱信息，在融合算法中采用了对比度与脉冲耦合神经网络相结合的方法来完成融合系数的选择.

1 图像小波的分解

Mallat在Burt和Adelson的塔形图像分解和重构算法的启发下，提出了小波变换的Mallat快速算法.若设H（低通）和G（高通）为两个一维镜像滤波算子，其下标r和c分别对应于图像的行和列，则按照二维Mallat算法，在尺度j－1上有如式（1）的Mallat分解公式：

其中，Cj，D1j，D2j，D3j分别对应于图像Cj－1r低频成分、垂直方向上的高频成分、水平方向上的高频成分和对角方向上的高频成分.与之相应的二维图像的Mallat重构算法如式（2）：

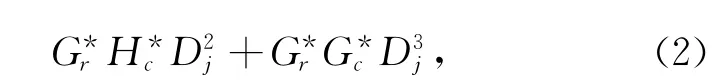
其中，H＊和G＊分别为H和G的共轭转置矩阵［3，8］.

为了使图像在分解和重构过程中，损失的信息更少，本文对Daubechies（DBN）、Coiflets（coiefN）、Syslets（symN）、Discrete Meyer wavelet（dmey）、BiorSplines（biorNr.Nd）小波基进行了对比，最后选取了DB1作为本文小波变换的小波基［9］.

2 图像处理中的PCNN模型

PCNN是由若干个神经元互相连接而成的反馈型网络，其每一神经元由3部分组成：接收部分、调制部分和脉冲产生部分.PCNN用于图像处理时，是一个单层二维的局部连接的网络，神经元的个数等于输入图像中的像素点的个数，神经元与像素点一一对应.为了更好地将其用于图像处理，人们提出了各种改进模型.本文采用的是文献［2］中提出的一种简化模型，其数学方程描述如式（3）所示：

其中，i，j是神经元的标号，Fij（n）是（i，j）神经元在第n次迭代时的反馈输入，Iij（n）为外部输入刺激信号（在图像处理中，则为第（i，j）个像数的灰度值）；Lij（n）是神经元的链接输入，β是链接强度，T为阈值，Uij（n）是神经元的内部行为，Yij（n）则是第n次迭代时（i，j）神经元的输出；w为神经元之间的连接权系数矩阵，VL是连接输入的放大系数；θij和Vθ是变阈值函数输出和阈值放大系数，αL和αθ分别为链接输入和变阈值函数的时间常数.n表示迭代次数.如果Uij（n）大于θij（n），则神经元产生一个脉冲，称为一次点火.事实上，n次迭代以后，人们常利用（i，j）神经元总的点火次数来表示图像对应处的信息.经过PCNN点火，由神经元总的点火次数构成的点火映射图作为PCNN的输出［5－7］.

3 图像的融合算法

3.1 算法步骤

本文融合算法的步骤如下：

1）对多光谱图像进行IHS变换，将其分解为强度I、色调H和饱和度S的3个近似正交分量，并将高分辨率图像与强度分量I进行直方图像匹配；

2）对匹配后的高空间分辨率图像和强度分量I进行小波分解；

3）为了提高图像的对比度和边缘特殊，小波分解后的低频系数采用基于边缘的选择方案；

4）小波分解后的高频系数采用改进的PCNN融合算法；

5）最后将融合得到的I分量进行小波反变换得到I，再结合色调分量H、饱和度分量S进行IHS反变换得到最后融合结果.

3.2 低频系数融合方法

图像低频的变化反映图像的信息量和清晰程度，低频变化越大的图像越清晰.一方面，低频信息包含图像的大量信息，是图像变化缓慢的部分，然而经典算法往往注重研究高频信息的变化特性，而忽略低频信息的变化，这会导致融合图像的对比度不高、图像模糊.另一方面，图像的低频为图像中变化缓慢的分量，仅仅考虑其变化会在一定程度上造成图像的斑点效应.本文采用Laplacian算子来对低频系数进行融合可以克服大多数频率域算法因为忽略了图像低频变化对图像的影响而导致的图像清晰度不够的缺点.

3.3 高频系数融合方法

在选择高频系数时，由于传统的基于PCNN的图像融合中，所有神经元的链接强度都取相同的数值，但是在人眼视觉系统中，视觉对于特征明显区域的反应比特征不明显的区域反应强烈，不可能每个神经元的链接强度都相同.因此，我们有理由认为PCNN中神经元链接强度的取值与对应像素的特征有一定的关系，而不是固定的常数.

为了得到更合理的PCNN神经元链接强度的取值，本文采用基于小波方向对比度作为PCNN神经元链接强度的值.文献2在研究对比度金字塔时提出了局部亮度对比度的定义，如式（4）所示：

式中，L为图像局部亮度；LB为图像的局部背景亮度，可以认为低频分量，LH＝L－LB是局部亮度减去局部背景得到的局部细节，可以认为是高频分量，文献3结合式（4）表达的意义，定义了小波对比度如式（5）：

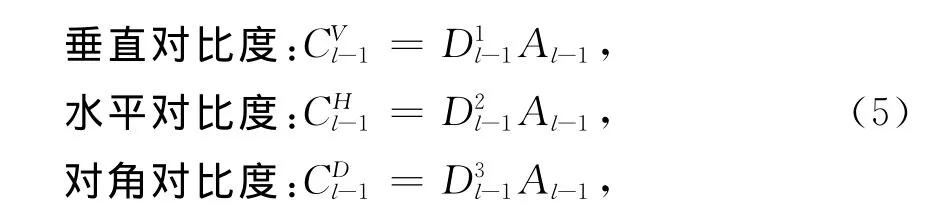
式中，Al－1为图像在2j－1分辨率上的低频近似分量；为图像在2l－1分辨率上的垂直高频细节；为图像在2l－1分辨率上的水平高频细节；为图像在2l－1分辨率上的对角高频细节.经过式（5）的计算得到了在2l－1分辨率上的对比度值分别为

改进的基于PCNN的融合步骤如下：

1）利用式（5）计算在2l－1分辨率上的垂直方向、水平方向和对角方向上的对比度值；

2）将以上的对比度值分别作为2l－1分辨率在不同方向上PCNN中相应神经元的链接强度值；

3）根据式（3）计算每个方向上的PCNN的点火次数；

4）最后比较两幅图像的点火次数来选择高频系数.

4 实验结果与分析

为了验证算法的有效性，本文选取一组全色光图像和多光谱图像进行融合试验.将本文算法（方法4）与目前图像融合处理中常用的Laplacian金字塔方法（简称为方法1）、传统的基于小波方法（简称方法2）和传统的基于NSCT的融合方法（简称为方法3）作比较；其中方法1和方法2中融合规则都采用低频系数取平均值，高频系数采用区域能量法；方法3中的低频系数采用平均值，高频子带系数采用边缘法.

图1 多光谱与全色图像及融合结果Fig.1 Multispectral image，Panchromatic image and the fusion results of every method.

实验结果如图1所示，图1（a）为多光谱图像，图1（b）为全色图像，图1（c）为方法1融合结果，图1（d）为方法2融合结果，图1（e）为方法3融合结果，图1（f）为本文算法融合结果.从视觉效果方面看：在频谱信息表现方面，3种方法得到的融合结果分别有不同程度的颜色失真，其中方法1较为严重，相反地，本文方法得到的融合效果较好；在空间细节信息表现方面看，3种方法和本文方法得到的效果都较好.

为了进一步对融合效果进行评价，本文采用熵、标准差、互信息和光谱所扭曲度客观评价指标对上述四种方法进行客观比较.其中熵是图像信息丰富程度的一个重要指标；图像的标准差反映了图像像素值的分布情况；互信息是计算源图像有多少信息转移到了融合结果中，数值越大，说明融合结果越好；图像的扭曲度则直接反映了多光谱图像的光谱失真程度，光谱扭曲度越大，这表明其光谱信息保持最差.通过表1中可知，不同的融合方法得到熵、互信息、标准差、光谱扭曲度的值都不同；通过比较，本文算法在熵、互信息、标准差、光谱扭曲度的指标中效果都是最好的；需要注意的是，该算法性能的提高是以复杂度的增加作为代价的.

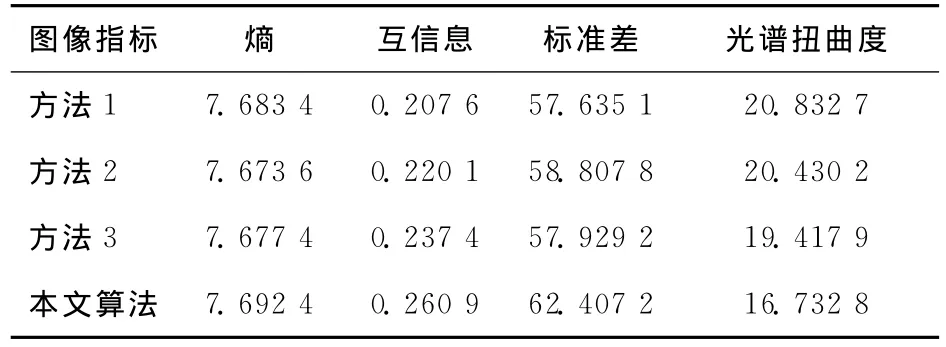
表1 融合算法性能的比较Fab.1 Compare of the fusion algorithm

5 结论

图像对比度的变化反映了图像内各个对象的差异，更加适合人眼的生理视觉特点；神经元的链接强度β反映网络中神经元之间耦合关系的强弱.本文提出的基于小波分解的自适应PCNN遥感图像融合算法，是在PCNN神经网络脉冲数（即点火次数）基础上采用基于小波方向对比度作为PCNN神经元链接强度的值，用符合人类视觉特性的图像对比度来进行调节，是一种可调节链接强度的图像融合算法.仿真实验表明，该算法在融合后的图像中空间结构信息和光谱信息都得到明显的提高，说明该算法有效、可行、性能良好，对于进一步深入研究利用PCNN及小波变换实现图像融合有重要的意义.

［1］Zhongni Wang，Xianchuan Yu.A Remote Sensing image fusion algorithm based on constrained nonnegative matrix factorization［J］.Image and Signal Processing，2008，672－676.

［2］Shaohui Chen，Renhua Zhang.SAR and multispectral image fusion using generalized IHS transform based on a trous wavelet and EMD decompositions［J］.Sensors Journal，2010，10（3）：737－745.

［3］陈 浩，王延杰.基于小波变换的图像融合技术研究［J］.微电子学与计算机，2010，27（5）：39－41.

［4］Zhenhua Li，Henry Lenug.Fusion of multispectral and panchromatic images using a estoration－based method［J］.2009，47（5）：1482－1491.

［5］李美丽，李言俊，王红梅，等.基于NSCT和PCNN的红外与可见光图像融合方法［J］.光电工程，37（6）：90－95.

［6］王志慧，赵保军，沈庭芝.基于MMPN和可调节链接强度的图像融合［J］.电子学报，2010，38（5）：1162－1166.

［7］苗启广，王宝树.一种自适应PCNN多聚集图像融合新方法［J］.电子与信息学报，2006，28（2）：466－470.

［8］王 丽，卢 迪，吕剑飞.一种基于小波方向对比度的多聚集图像融合方法 ［J］.中 国图象 图形 学报，2008，13（1）：145－150.

［9］龚建周，刘彦随，夏北成，等.小波基及其参数对遥感影像融合图像质量的影响［J］.地理与地理信息科学，2010，26（2）：6－10.

［10］吴 艳、李 明，杨万海，等.多光谱与高分辨率图像融合的新算法［J］.西安电子科技大学学报：自然科学版，2008，35（4）：696－702.

［11］洪日昌，吴秀清，袁 勋.基于双正交多小波变换的多光谱与全色图像融合研究［J］.中国图象图形学报，2007，12（4）：684－690.