考虑努力及退货价格因素的易逝品供应链弹性数量契约模型

覃艳华

（电子科技大学 中山学院 经济与管理学院，广东 中山 528402）

考虑努力及退货价格因素的易逝品供应链弹性数量契约模型

覃艳华＊

（电子科技大学 中山学院 经济与管理学院，广东 中山 528402）

考虑由一个制造商和一个零售商组成的易逝品供应链，在销售努力水平及退货价格与需求及退货具有相关性的前提下，建立了易逝品供应链的弹性数量契约模型，指出单纯的弹性数量契约无法实现供应链协调，而基于回馈与惩罚契约策略下的弹性数量契约能够实现供应链协调，并给出了供应链协调下的模型优化方法；最后，以数值实例计算了易逝品供应链协调下的最优销售努力水平、最优退货价格和最优订购量，并分析了各种参数的变动对最优退货价格、最优销售努力、最优订购量和集成式供应链最优利润的影响.

易逝品供应链；弹性数量契约；回馈与惩罚策略；协调

弹性数量契约是指制造商允许零售商在观察市场需求之后可以改变最初订购量的协议.通常是制造商在销售季节前让零售商预订产品数量，制造商据此组织生产，当零售商进一步获取市场信息后，允许零售商在制造商所能提供的产品数量范围内确定其最终订购量.弹性数量契约在电子和计算机产业中得到了广泛运用，如IBM、HP、Compaq等大公司.杨德礼等人［1］认为弹性数量契约的研究主要集中的3个方面：一是零售商应采取何种订货方式；二是制造商如何制定契约并组织生产；三是制造商和零售商如何对收益进行分配.Signorelli和 Heskett［2］在哈佛商学院案例中用Benetto公司作为典型案例，来说明对销售商实施弹性数量契约不但可以增加销售商的利润，而且也可以增加供应商的利润.近年来有关弹性数量契约建模方面的研究正呈增长趋势，如Lariviere［3］建立了单周期弹性数量契约模型；Tsay［4］则把单周期模型扩展到多周期销售情况中，建立了多周期弹性数量契约模型；Eppen和Iyer［5］研究了基于回馈下的上游弹性数量价值；Tsay和Lovejoy［6］分析了多级、多周期供应链模式并结合需求预测更新，探讨了弹性数量契约对供应链绩效的影响.

但从目前大量的有关文献中可以看出，大多数文献都没有考虑零售商销售努力及无缺陷退货［7］价格对需求和退货的影响，这与实际情况是不相符的.在现实生活中，销售努力水平与无缺陷退货价格是影响需求和退货的最重要的两个因素［8-9］.零售商通过向消费者耐心说明产品的特点、功能，演示产品的操作使用方法等销售努力不仅可以扩大需求，而且可以减少无缺陷退货；同时是否允许无缺陷退货及退货价格的高低也将对需求和退货同时产生影响.由于销售努力和无缺陷退货都需要成本，因此制造商和零售商之间将产生一定的冲突，导致这个问题产生的原因是销售努力和退货价格因素对整个供应链有利，而对零售商来说却是要付出成本的.为此，Cachon［10］分别证明了需求和价格、需求和努力因素具有相关性下，弹性数量契约无法实现供应链协调的最优目的，但他们没有给出解决这一问题的方法；何勇等人［11-12］研究了需求与销售努力具有相关性下的利益共享模型及退货政策模型，指出单纯的利益共享契约或单纯的退货契约无法实现供应链协调，而在此基础上引入回馈与惩罚策略可以实现供应链协调；姬小利［13］研究了需求与销售努力具有相关性下的基于回购契约的促销成本分摊契约协调机制；Ferguson等人［7］考虑到了零售商的销售努力对无缺陷退货的影响，进而研究了基于无缺陷退货下单个制造商和单个零售商组成的供应链的协调问题.但这些文献只考虑了零售商销售努力对需求或对退货的影响，而没有考虑零售商的销售努力将同时对需求和退货都产生影响，而且也没有考虑无缺陷退货价格对需求及退货产生的影响.该文正是基于此问题，在销售努力及无缺陷退货价格都与需求及无缺陷退货具有相关性的前提下，对弹性数量契约进行数学建模和分析，找出问题的解决途径.

1 问题描述与假设

2 模型的建立与分析

2.1 集成式供应链下的模型

根据前面的假设可得集成式供应链的期望利润为

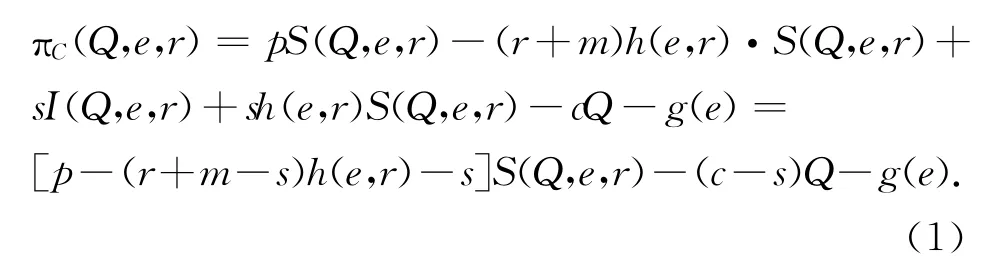
设r＊为在给定订货量和努力水平下的最优退货价格，则r＊必须满足下面条件：

设e＊为在给定订货量和退货价格下的最优努力水平，则e＊必须满足下面条件：

设Q＊为在给定退货价格和努力水平下的最优订货量，则Q＊必须满足下面条件：

根据供应链协调的要求，（2）式、（3）式和（4）式是收益共享契约实现供应链协调的必要条件.

2.2 弹性数量契约模型

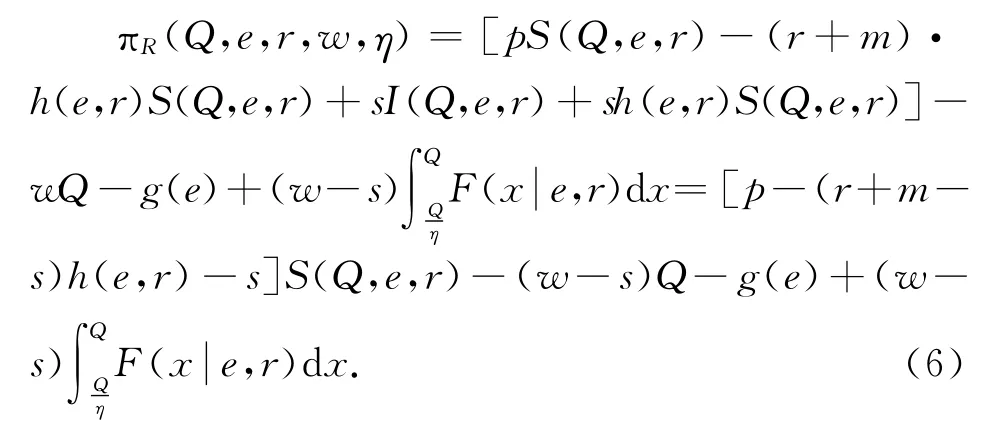
要实现供应链协调，则分散式供应链下的退货价格及努力水平与集成式供应链下的退货价格及努力水平一致，故集成式供应链下的最优退货价格r＊和最优努力水平e＊必须分别满足下面的条件：弹性度，则在弹性数量契约模式下销售商的期望利润为

比较式子（7）和式子（2）、式子（8）和式子（3）可以发现，只有当w＝s时，式子（7）和（8）才能成立.然而，当w＝s时，制造商将获得负的利润.由此可见，当需求及退货与退货价格及努力水平具有相关性的情形下，单纯的弹性数量契约无法实现供应链协调的目的.

2.3 基于回馈与惩罚策略的弹性数量契约模型

为解决上述问题，这里提出了基于回馈与惩罚策略的弹性数量契约模型，通过下面的分析可以发现，在弹性数量契约中引入回馈与惩罚策略，能够很好地解决该问题.所谓回馈与惩罚策略，就是制造商给零售商分别提供一个销售目标和一个顾客无缺陷退货目标，如果零售商超额完成销售任务，制造商就给予超额部分以奖励，否则，将对没有完成销售任务的部分进行惩罚；同时，如果零售商的顾客无缺陷退货低于顾客无缺陷退货目标，制造商就给予低于目标的部分以奖励，否则，对高于目标的部分进行惩罚.假设制造商提供的销售目标为H，在销售期结束后，对销售量超过H以上的部分，制造商给予零售商每件产品的回馈为λ，对于没有完成任务的部分，制造商对零售商每件产品的惩罚也为λ；假设制造商提供的顾客无缺陷退货量目标为T，销售季节结束后，对顾客无缺陷退货量小于T的部分，制造商给予零售商每件产品的回馈为τ，对顾客无缺陷退货量超过T的部分，制造商对零售商每件产品的惩罚也为τ.则在弹性数量契约中引入回馈与惩罚策略时，零售商的期望利润为：

根据供应链协调的要求，集成式供应链下的最优退货价格r＊和最优努力水平e＊必须分别满足下面的条件：

比较式子（10）和式子（2）、式子（11）和式子（3）可知，要使上面两式成立，则

式（12）表达了最优决策变量λ，τ，w，r和e之间的关系.由式子（9）可知，在供应链协调的情况下，弹性数量契约模式的最优订货量Q＊必须满足下式

这里，制造商可通过调整α和δ的大小，进而即调整η的大小使得w≥c，从而确保制造商可以获利.

联合求解式子（12）和（14）可求出最优的回馈与惩罚因子λ＊、τ＊和最优的批发价格w＊.进一步，，制造商可调整给零售商销售目标H和退货目标T的大小，使得引入回馈与惩罚策略后零售商及制造商的利润不低于没有引进回馈与惩罚策略下的利润（这里，可通过对比引入回馈与惩罚策略及没有引入回馈与惩罚策略下的零售商及制造商的收益，确定制造商给予零售商的销售目标和退货目标值，使得制造商和零售商双方都有动力参与供应链协调，由于这不是本文研究的重点，因而在这里不作相关推导）.综上可见，在需求及退货与努力水平及退货价格具有相关性的前提下，通过在弹性数量契约中引入回馈与惩罚策略，并确定合适的销售目标H和退货目标T，就可以实现供应链协调，且契约参数满足式（12）和（14）.

3 模型优化方法

由上节分析可知，通过在弹性数量契约中引入回馈与惩罚策略，可以实现供应链协调，

并能确保零售商的订购量、努力水平和退货价格与集成式供应链模式下一致，因此，模型的优化问题变为：寻求最优的Q＊、r＊和e＊，使式子（1）的值最大.

为了便于模型优化，假设易逝品的市场需求函数为x＝y（e，r）＋ε，其中y（e，r）是由销售努力与退货价格共同决定的期望需求量，根据实际情况，易知y（e，r）为零售商销售努力e的增函数，且为凸函数，即≤0；y（e，r）为退货价格r的增函数，且为凸函数，即＞0，≤0；ε为独立于e和r的随机变量，并用f（ε）代表ε的概率密度函数，F（ε）表示ε的累积分布函数.此时，需求x的概率密度函数和累积分布函数分别为＝f（x－y（e，r））和＝F（x－y（e，r））.则期望销售量S（Q，e，r）＝Q－代入式子（1）可得

从式子（15）可知，对于给定的e和r，πC（Q，e，r）相对于Q为凸函数，有最优解，则最优解Q＊满足下式

把式子（17）和ε＝x－y（e，r）代入式子（15），整理可得

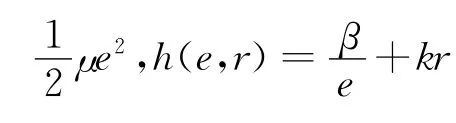
根据实际情况可知供应链是可实现最优的，也就是说πC（Q（e，r），e，r）是关于r和e的凸函数.由此可得最优退货价格r＊和最优销售努力e＊满足下列式子

联合解式（20）和（21），利用 Matlab工具可求出最优退货价格r＊和最优销售努力e＊，把r＊和e＊代入式子（17）可求解出最优订货量Q＊.

4 实例计算与分析

根据易逝品市场的实际情况和实现供应链协调的相关条件，假设p＝30，c＝5，s＝1，a＝10，h＝20，β＝0.08，x0＝100，b1＝5，b2＝3，μ＝10，k＝0.01，m ＝0.05.由式子（21）、（20）和（17）可分别求得e＊＝11.54，r＊＝15.35和Q＊＝222，由式子（19）可得最优的集成供应链利润πC（Q＊，e＊，r＊）＝4417.2.

通过分析可以进一步得到，各参数变化与最优退货价格、最优努力水平、最优订货量、集成式供应链的最优利润的关系如表1所示.

由此可见，在弹性数量契约中引入回馈与惩罚策略，可以实现供应链的协调，同时可以发现给顾客无缺陷产品全价退货或不退货都不是一个最好的选择，而且制造商或零售商应该根据单位产品生产成本c、单位剩余产品的残值s、单位产品的市场销售价格p、退货成本m、销售努力激发的退货弹性β、退货价格激发的退货弹性k、销售努力激发的需求弹性b1和退货价格激发的需求弹性b2来确定最优的顾客无缺陷退货价格和最优销售努力水平；同时，制造商或零售商还可以通过调整单位生产成本、改变剩余产品的处理方式以及控制产品销售价格、退货成本等手段，改变最优的顾客退货价格和最优销售努力水平，从而扩大市场需求，最终提高整个供应链的利润.

表1 各参数变化与最优退货价格、最优销售努力、最优订货量、集成供应链利润的关系Tab.1 The relationship between parameter changes and the optimal return price，the optimal sale effort，the optimal order quantity，integrated supply chain relationships

5 结论

该文在需求不确定的条件下，将顾客无缺陷退货价格及零售商销售努力因素对需求和退货率的影响引入易逝品供应链，发展了易逝品正向物流和退货逆向物流并存系统的协调模型，指出单纯的弹性数量契约并不能实现供应链协调，而基于回馈与惩罚策略下弹性数量契约能够实现供应链的协调；给出了在供应链协调下的模型优化方法，并用数值实例计算了易逝品供应链协调下的最优退货价格、最优销售努力水平及最优订货量，并比较分析了最优退货价格、最优销售努力、最优订货量及集成式供应链最优利润与单位生产成本、单位剩余产品残值、单位产品市场销售价格、单位退货成本、销售努力激发的退货弹性、退货价格激发的退货弹性、销售努力激发的需求弹性及退货价格激发的需求弹性之间的变动关系，进而为供应链的决策者进行科学决策提供了依据.

［1］杨德礼，郭 琼，何 勇，等.供应链契约研究进展［J］.管理学报.2006，3（1）：117－125.

［2］Sigorelli S，Benetton Heskett J L.Harvard business school case 9－685－0141［M］.TN：Harvard Business School Press，1984：12.

［3］Lariviere M A.Supply chain contracting and coordination with stochastic demand，quantitative models for supply chain management［M］.Boston：Kluwer Academic Pubishers，1999：233－268.

［4］Tsay A A，Lovejoy W S.Quantity flexibility contracts and supply chain performance［J］.Manufacturing and Service Operations Management，1999，1（2）：89－111.

［5］Eppen G，Iyer A.Backup agreement in fashion buying－the value of upstream flexibility［J］.Management Science.1997，43（11）：1469－1484.

［6］Tsay A A ，Lovejoy W S.Quantity flexibility contract s and supply chain performance ［J］.Manufacturing and Service Operations Management，1999，1（2）：89－111.

［7］Ferguson M，Jr V G，Souza G.Supply chain coordination for false failure returns returns［J］.Manufacturing ＆ Service Operations Management.2006，8（4）：376－393.

［8］Taylor T A.Supply chain coordination under channel rebates with sales effort effects［J］.Management Science，2002，48（8）：992－1007.

［9］Samar K M，Robert S.Reverse logistics in e－business optimal price and return policy［J］.International Journal of Physical Distribution ＆ Logistics Management.2004，34（1－2）：70－88.

［10］Cachon G P.Supply chain coordination with contracts［M］.In de A G Kok ＆Graves S C（Eds），Handbooks in Operations Research and Management Science，North Holland：Elsevier，2003，11：227－339.

［11］何 勇，杨德礼，孟丽菊，等.考虑努力因素的退货政策模型［J］.系统工程理论方法应用.2005，14（6）：568－571.

［12］何 勇，吴清烈，赵林度.考虑努力及价格因素的弹性数量契约模型［J］.系统工程与电子技术.2007，29（12）：2056－2059.

［13］姬小利.伴随销售商促销努力的供应链契约设计［J］.中国管理科学.2006，14（4）：73－76.ment of the Baltic Sea［J］.Mar Pollut Bull，1995，31（4／12）：237－248.

［15］Nisbet c，Lacoy P.Toxic Equivalency Factors（TEFs）for Polycyclic Aromatic Hydrocarbons（PAHs）［J］.Regul Toxicol Pharmacol，1992，16：290－300.

Distribution and ecological risk assessment of PAHs in road dust of Guiyang urban area

WANG Ya1，HE Huazhong1，LING Ye2，YANG Chen1，YAN Min1，WANG Yajie1
（School of Chemistry and Environmental Science，Guizhou University for Nationalities，Guiyang 550025）

In the present study，16polycyclic aromatic hydrocarbons（PAHs）in road dust of Guiyang urban area were quantitatively determined by HPLC.Distribution characterization and possible sources of PAHs in road dust from Guiyang urban area were analyzed.The ecological risks of PAHs in road dust of Guiyang urban were assessed according to the single index，N.L.Nemerow composite index and benzo［a］pyrene equivalency quality（BEQ）methods.The results showed The content of total PAHs were between 88.1and 13192.7μg／kg.The difference of PAHs concen－trations in road dust from functional areas were also obvious.PAHs concentrations in road dust were higher at traffic area than those in other areas.Evaluation of the ecological risks of PAHs in the study area indicated that there were heavily polluted by PAHs at traffic area and industrial estate.

road dust；polycyclic aromatic hydrocarbons（PAHs）；distribution；ecologicalrisk

F274

A

1000－1190（2012）04－0477－06

2012－04－12.

广东省自然科学基金项目（10152840301000001）；电子科技大学中山学院科研团队培育基金项目（411YT01）.

＊E－mail：kejian200609＠163.com.