晋西黄土区刺槐人工林林冠截留模拟

王晓燕，毕华兴，高路博，朱悦，刘李霞

(北京林业大学水土保持学院;水土保持与荒漠化防治教育部重点实验室;山西吉县森林生态系统国家野外科学观测研究站:100083，北京)

黄土高原严重缺水，且水资源年内分布不均匀，生态环境恶化，是世界上水土流失严重地区之一。为改善其生态环境，缓解人口、资源、环境的矛盾，新中国成立以来，国家投入了大量的人力、物力、财力，实施了各种林业生态工程。林冠截留作为森林水文过程中的一环，是降雨到达地面过程中发生的第1次水量分配，这一过程可以对降雨产生滞留作用，缓解雨滴对地表土壤的冲击力，并且还影响营养元素的输入，在森林水文循环过程中占据重要地位。林冠截留模型是估算和预测林冠截留的有效工具，根据影响林冠截留的各个因子与林冠截留的关系，国内外学者推出了许多林冠截留模型。以A.J.Rutter等［1］为代表的概念模型，由于考虑了林分结构和气象因子对降雨的影响，能够估算降雨期间和降雨停止后的截留损失，可以在一定程度上应用到其他林分;但此模型需要大量具有物理意义的参数，仍然导致模型在应用上受到一定的限制。在Rutter 模型的基础上，J.H.C.Gash 等［2－3］借助简单的经验公式，形成了便于使用的Gash 解析模型，并于1995 年引入冠层覆盖度参数对原模型进行了改进。改进后的模型能更好地模拟实际的林冠特征，更适应于不同森林类型林冠截留模拟的研究［3－6］。刺槐(Robinia pseudoacacia) 是晋西黄土区的主要造林树种之一。笔者通过应用修正的Gash 模型，模拟蔡家川流域刺槐人工林林冠截留的特征，以期为晋西黄土区刺槐人工林生态水文过程和影响机制研究提供理论基础，并为刺槐人工林的经营和管理提供科学依据。

1 研究区概况

研究地点位于山西省吉县森林生态系统国家野外科学观测站蔡家川流域，E110°39'45″～110°47'45″，N36°14'27″～36°18'23″，海拔904 ～1 592 m，温带大陆性气候，年均温10.3 ℃，年均降水量489.10 mm，降雨最大月份出现在7、8 月份。全年日照时间2 564.10 h，无霜期172 d。土壤以褐土为主。

2 研究方法

2.1 试验样地的设置

在蔡家川流域人工刺槐林林地选择具有代表性地段设立1 个20 m×20 m 的人工刺槐林标准样地，样地坡度20°，坡向南偏东34°。树龄为15 年生同龄林，林木密度为1 800 株/hm2，郁闭度0.8，平均树高5.71 m，胸径6.35 cm，林下灌木较少，零星分布有黄刺玫(Rosa xanthina Lindl.)、胡颓子(Elaeagnus)等，林下主要草本有铁杆篙(Tripolium vulgare Nees)、萝摩(Metaplexis japonica(Thunb.) Mak.)、羊胡子(Eriophorum)等。

2.2 修正的Gash 模型

修正的Gash 模型［2－3］将降雨描述为一系列彼此分离的事件，在假定2 次降雨事件之间有足够的时间让林冠干燥到降雨前程度的前提下，每个降雨事件包含林冠加湿过程、林冠达到饱和并维持饱和状态的过程及降雨停止后林冠干燥过程3 个阶段，总的林冠截留量由林冠在整个降雨过程中各个阶段的截留损失量相加得到。

修正的Gash 模型有以下几个基本假设［2－3］条件:1)雨滴在林冠饱和后从林冠滴落;2)林冠饱和之后方有树干茎流发生;3)树干蒸发发生在降雨停止后;4)将林地划分为有植被覆盖区域和无植被覆盖区域，蒸发只发生在有植被覆盖区域，且蒸发只发生在一维垂直空间上。

对于冠层未饱和的m 次降雨

对于冠层达到饱和的n 次降雨

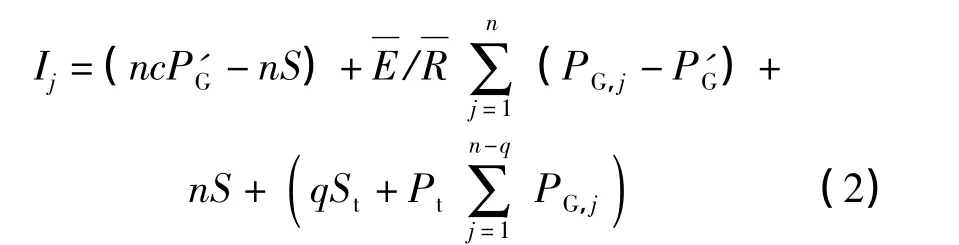
式中:Ij为林冠截留量，mm;c 为林分郁闭度;m 为降雨量使林冠未达到饱和的降雨次数;PG，j为第j 次降雨事件的林外降雨量，mm;n 为降雨量使林冠达到饱和的降雨次数; P'G为使林冠达到饱和的降雨量，mm;S 为林冠持水能力为降雨期间林冠达到饱和后的平均蒸发速率，mm/h;为降雨期间平均降雨强度，mm/h;q 为降雨量使树干达到饱和产生树干茎流的降雨次数;St为树干持水能力，mm;Pt为树干茎流系数。

2.3 修正的Gash 模型各参数的计算方法

1)St和Pt由树干茎流量与林外降雨量的关系方程确定，树干茎流量与林外降雨量关系方程在y 轴截距的负值为St，Pt为斜率［7］。

2)林冠持水能力S 的确定是根据林内穿透雨量与林外降雨量关系方程，求得穿透雨量的残差，之后根据林外降雨量(PG)与穿透雨量残差的关系，推求方程穿透雨量残差大于0 所对应的最小林外降雨量值，用大于此值且残差穿透雨量残差大于0 的降雨量与对应的林内穿透雨量做回归方程，林冠持水能力(S)即为方程在x 轴截距的负值［7-8］。

3)降雨期间林冠达到饱和后的平均蒸发速率E的计算公式［2］为

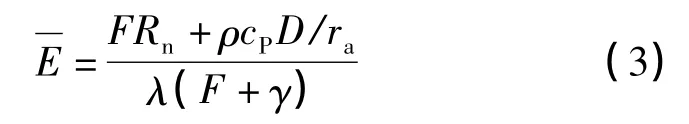
式中:F 为饱和水汽压梯度，hPa/℃，F=40 980Ps/(237.3+θ)2，其中Ps为饱和水汽压，hPa，θ 为温度，℃; Rn为大气净辐射，W/m2;ρ 为空气密度，g/m3，ρ=1.276×273pa/(θ+273)，其中pa为大气压强，hPa;cp为空气在常压下的比热容，1.004 8 J/(g·℃);D 为饱和水汽压差，hPa，即气温(θ)对应的饱和水汽压(ps)与同温度对应的实际水汽压(pT)之差(D= ps－pT);ra为空气动力学阻力，s/m;λ 为 水 的 汽 化 潜 热，J/g，λ = (2.51 －0.002 361θ)×1 000;γ 为空气湿度常数，hPa/℃，γ=1.614 52P/λ。

饱和水汽压ps由马格努斯饱和水汽压公式计算，即

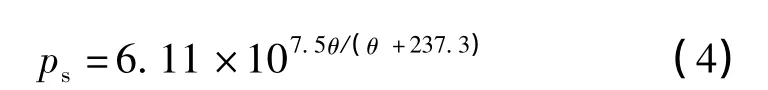
实际水汽压pT为空气相对湿度与饱和水汽压的乘积。

空气动力学阻力ra的计算公式［9］为

式中u 为树冠上方2 m 处的风速，m/s。u 的计算公式［9］为

式中:u0为测定点风速，m/s;z 为观测点距离地面的高度，m。

4)使林冠达到饱和所必需的降雨量P'G由下式［3］确定:

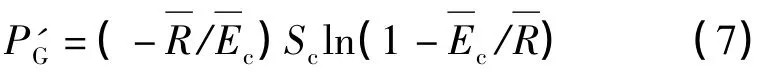
5)为求得使树干达到饱和产生树干茎流的降雨次数q，需得知使树干达到饱和所必需的降雨量P″G。P″G 的计算公式［7］为

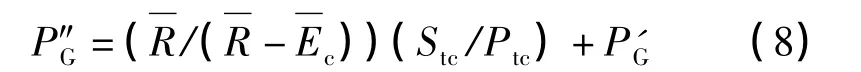
式中: Stc=St/c;Ptc=Pt/c。

2.4 林分参数的测定方法

1)林内穿透雨量:于2007 与2008 年7—10 月份，通过在研究区20 m×20 m 的刺槐试验林标准地内随机布设的100 cm×20 cm 的10 个承雨槽收集林内穿透雨量，承雨槽高出地面约10 cm，且与地面保持约有1°的倾角，较低的一端用胶管与10 L 塑料桶相连。每次降雨前将承雨槽内的枯枝树叶清除掉，雨后用量筒测量塑料桶内的雨水体积(mL)，然后换算成mm。

2)在刺槐林标准地内，按照4 ～8 cm 的径级分布，按2 cm1 个径级(其中6 cm 径级选择2 株标准木，其他选择1 株)选择标准木4 株，测量其树干茎流量。

在距离树干基部1 m 处，将直径1.8 cm 的聚乙烯塑料软管剖开后用铁钉固定在树干上，然后在树干上(树皮被修整光滑)围绕2 ～3 周，用玻璃胶将塑料软管与树干的接缝处封严，塑料软管下端接入塑料桶，每次降雨后用量桶量测桶内的水量(mL)。树干茎流量的计算公式为

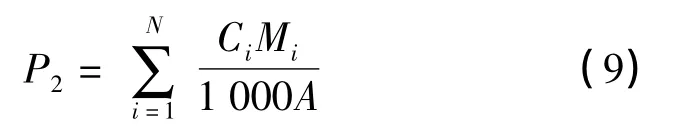
式中:P2为样地树干径流量，mm;N 为树干径级数;Ci为径级i 的树干茎流体积，mL;Mi为径级i 的树木株数;A 为样地面积，m2。

3)林外降雨和气象参数由布设在林地外的美国产Campell－Scientific 系列全自动气象站测出，观测林外降雨量(mm)、空气温度(℃)、空气湿度(%)、风速(m/s)、大气净辐射(W/m2)和大气压强(hPa)等数据，每10 min 记录1 次，精度可满足模型的基本要求。

4)林冠截留量由实测大气降水量减去林内穿透雨量和树干茎流量得到。

3 结果与分析

3.1 降雨分配特征

为满足模型的假定条件，对2007 和2008 年7—10 月场降雨间隔时间大于8 h［5］的19 场降雨及林内穿透雨量、树干茎流量等进行统计，结果见表1。可以看出:林外总降雨量为455.20 mm，林内穿透雨量、树干茎流量和林冠截留量分别为349.94、9.62和95.64 mm，分别占林外总降雨量的76.88%、2.11%和21.01%;平均穿透率为77.44%，平均干流率为2.16%，平均截留率为20.40%。可知，人工刺槐林地的降雨大部分以穿透雨的形式直接降落到地面，另外极小部分以树干流的方式沿树干流向地面，还有一大部分被林冠截留，最后以蒸发的方式返回到大气中。研究结果与L.K.Rowe［10］、曹云等［11］、魏天兴等［12］研究得到的阔叶林林冠截留量为降水量的10.00%～35.00%相一致。

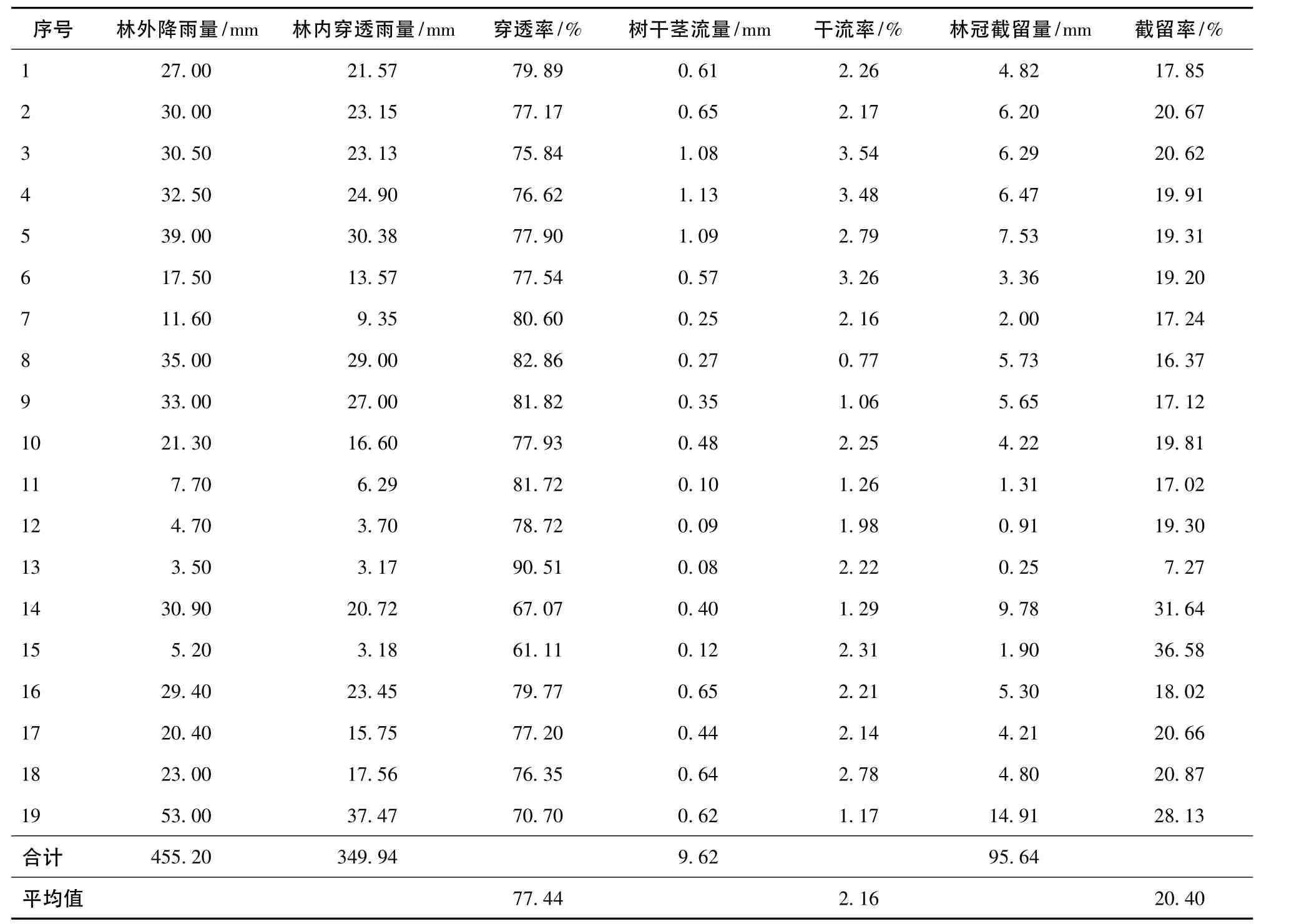
表1 刺槐人工林降雨分配情况Tab.1 Distribution of rainfall on Robinia pseudoacacia artificial forest

3.2 林冠截留模拟

3.2.1 模型林分参数的确定 刺槐林林内穿透雨量P1(mm)与林外降雨量的关系为

林外降雨量与穿透雨量残差的关系如图1 所示。由图得出，穿透雨量残差大于0 所对应的最小林外降雨量值为11.60 mm。大于11.60 mm 且穿透雨量残差大于0 的降雨量与对应的林内穿透雨量的回归方程为

即林冠持水能力S 为0.55 mm。

Gash 模型对林冠截留量模拟的准确性是以正确测出或估算林冠持水能力S 为基础的［7］。A.Deguchi 等［13］总结出多种乔木林S 值的变化范围为0.25 ～1.55 mm，何常清等［5］推算出四川卧龙亚高山栎林(Quercus aquifolioides)的S 为0.23 mm。笔者利用回归法推算出的林冠持水能力S 为0.55 mm，与前人推算出的S 值相似，因此，认为笔者推算出的S 值是合理的。

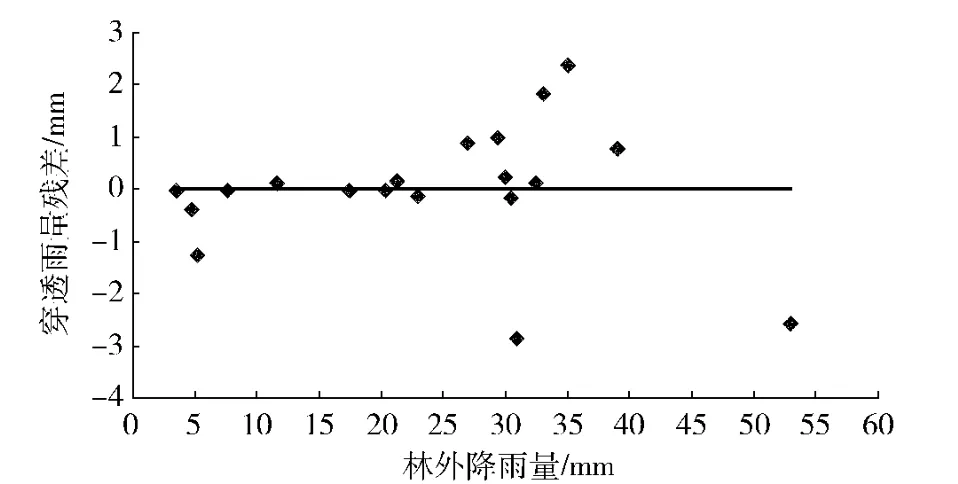
图1 刺槐穿透雨量残差与林外降雨量的关系Fig.1 Relationship between the residuals of throughfall and rainfall in Robinia pseudoacacia

刺槐林树干茎流量P2(mm)与林外降雨量的关系为

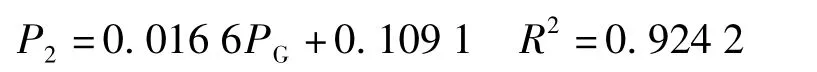
得出St为0.109 1 mm，Pt为0.016 6 mm。

3.2.2 模型降雨参数的确定 通过气象站测定，得到研究期间研究区林外总降雨量为455.20 mm，最大降雨量为53.00 mm，最小降雨量为3.50 mm，平均降雨强度0.67 mm/h。根据各气象参数的计算公式和式(3)，计算得到降雨期间林冠达到饱和后的平均蒸发速率为0.10 mm/h，根据式(7)和(8)，计算得出使林冠达到饱和的降雨量P'G 和使树干达到饱和所必需的降雨量P″G 分别为0.75 和8.70 mm。

3.2.3 模拟结果分析 修正的Gash 模型最初主要应用于林冠截留周累计量的估算［3］。林冠累计截留量的模拟值和实测值比较结果见图2 和图3。由图2 可以看出，模型可以较好地模拟刺槐人工林的林冠累计截留量，林冠累计截留量模拟值小于实测值，林冠最终累计截留量的模拟值为83.60 mm，占大气降雨量的18.37%，截流率比实测值低2.64%。由图3 可以看出，林冠累计截留相对误差最小值为0.76%，最大值为12.60%，平均为6.40%，相对误差小于6.60%的占36.80%，7.00%～8.00%之间的占36.80%，9.00%～10.00%之间的占21.10%，大于10.00%的占5.30%。

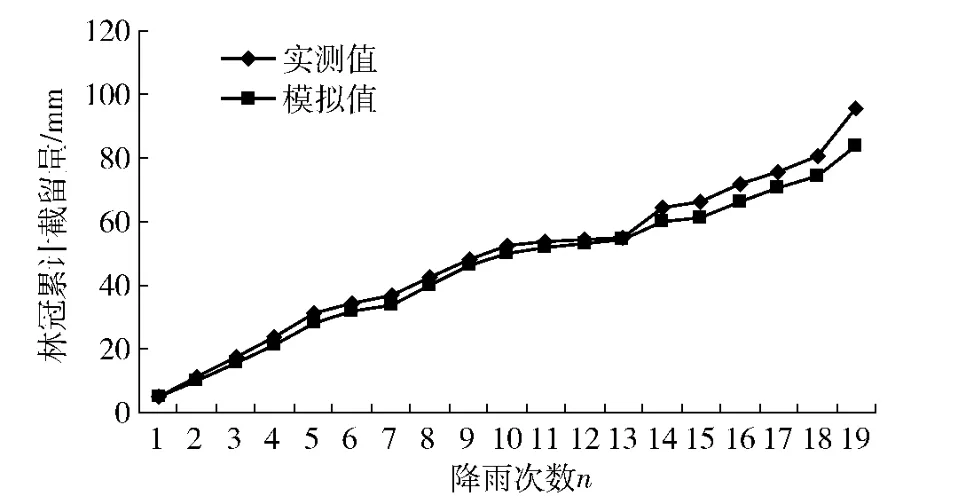
图2 林冠累计截留量模拟值与实测值比较Fig.2 Comparison of simulation and measured of cumulative amount of canopy interception

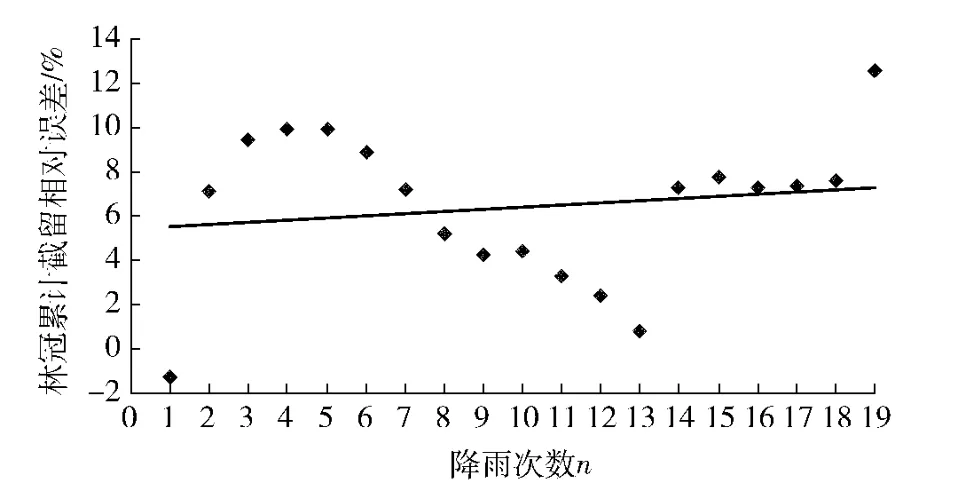
图3 林冠累计截留相对误差Fig.3 Relative error of cumulative canopy interception

应用修正的Gash 模型对次降雨的林冠截留量进行尝试性模拟，对于冠层未饱和的m 次降雨，用式(1)计算其林冠截留量，对于冠层达到饱和的n次降雨，参考式(2)，并将式(2)中降雨期间林冠达到饱和后的平均蒸发速率和降雨期间平均降雨强度用单场降雨期间的蒸发速率和降雨强度替代，其他参数不变。

场降雨的林冠截留量模拟结果见图4。可以看出，模型可以较好地模拟出部分场降雨的林冠截留量，模拟值与实测值最小相差0.02 mm;但个别场降雨的林冠截留量模拟效果较差，第14 和19 场降雨林冠截留量的模拟值和实测值相差最大，分别为4.28 和5.91 mm。

图4 场降雨林冠截留量模拟值与实测值比较Fig.4 Comparison of simulation and measured of canopy interception of one single rainfall event

4 结论与讨论

1)应用修正的Gash 模型可以很好地模拟晋西黄土区刺槐人工林的林冠累计截留量，平均林冠累计截留相对误差为6.40%，模拟出的刺槐林林冠累计截留量低于实测值。

刺槐林林冠累计截留量低于实测值的原因，可能是修正的Gash 模型在模拟林冠截留量时忽略了从林冠以滴落的形式到达地表的这部分雨量，且当大气降雨量PG小于林冠截留量P'G时，林冠截留量表示为冠层覆盖度乘以大气降水，在这个过程中，因没有考虑蒸发的影响，故与实际情况不符，从而使模拟值低于实测值。何常青等［5］应用修正的Gash 模型对岷江上游亚高山川滇高山栎林的林冠截留量进行了模拟，模拟值小于实测值。孙向阳等［6］同样用该模型对贡嘎山高山演替林的林冠截留量进行了模拟，结果显示2008 年的林冠截留量模拟值比实测值低，2009 年的模拟值与实测值吻合较好。笔者的研究结果与前人的研究结果具有较好的一致性。

2)在模拟场降雨过程中，修正的Gash 模型不能较好地模拟每场降雨的林冠截留量。

由于对于单场降雨的林冠截留量来说，由假设与实际自然条件的差异导致的模型误差更加明显。场降雨林冠截留量的模拟值与实测值相比，表现为部分场降雨林冠截留量模拟值大于实测值，部分小于实测值，可能是由于降雨量与降雨强度不同而至。孙向阳等［6］用该模型对次降雨林冠截留量的模拟结果表明，当降雨量较小时，模拟值略高于实测值，当降雨量较大时，模拟值低于实测值。由于修正的Gash 模型不能较好地模拟次降雨的林冠截留量，所以，对于降雨量与降雨强度对该模型模拟结果的影响，笔者不再作进一步研究。如何应用并改进修正的Gash 模型，使其可以对次降雨林冠截留量进行模拟，有待于今后基于大量详细观测资料的基础上进一步研究。陈涛［14］根据蔡家川流域多年林冠截留试验研究结果建立了林冠截留量的动态模拟模型，并对各林分类型的场降雨林冠截留量进行了模拟，结果显示，刺槐林的模拟林冠截留率比实测值小1.80%～6.10%，模拟效果较好。笔者建议，对晋西黄土区刺槐人工林场降雨林冠截留量的模拟应选用此林冠截留量动态模拟模型。研究中第14 和19 场降雨林冠截留量的模拟值与实测值间的差异之大异于其他，除以上原因外，还可能是由于实验过程中出现的人为失误等原因造成。

3)场降雨之间间隔的时间不同，模型中涉及的气象条件会发生变化，从而影响林冠截留量的蒸发和降雨强度等因子。

A.Deguchi 等［13］和T.E.Link 等［15］认为，E/R对林冠截留量的变化率的影响最大，可见，2 场降雨之间的时间间隔不同会严重影响到模型的模拟精度。借鉴前人的研究成果，选用间隔时间大于8 h的场降雨数据进行模型的模拟，结果显示，所得数据可以较好地进行修正的Gash 模型的林冠截留模拟。关于晋西黄土区刺槐林场降雨间隔时间不同对Gash 模型模拟精度的影响，有待于下一步继续研究。

［1］ Rutter A J，Kershaw K A，Robbins P C，et al.A predictive model of rainfall interception in forests:Ⅰ.Derivation of the model from observations in a plantation of Corsican pine［J］.Agricultural Meteorology，1971，9:367－384

［2］ Gash J H C.An analytical model of rainfall interception by forests［J］.Quarterly Journal of the Royal Meteorological Society，1979，105:43－55

［3］ Gash J H C，Lloyd C R，Lachaud G.Estimating sparse forest rainfall interception with an analytical model［J］.Journal of Hydrology，1995，170:79－86

［4］ Carlyle M，Osesa D E，Priceb A G.An evaluation of the Gash interception model in a northern hardwood stand［J］.Journal of Hydrology，1999，214:103－110

［5］ 何常清，薛建辉，吴永波，等.应用Gash 解析模型对岷江上游亚高山川滇高山栎林林冠截留的模拟［J］.生态学报，2010，30(5):1125－1132

［6］ 孙向阳，王根绪，李伟，等.贡嘎山亚高山演替林林冠截留特征与模拟［J］.水科学进展，2011，22(1):23－29

［7］ Limousin J M，Rambal S，Ourcival J M，et al.Modelling rainfall interception in a Mediterranean Quercus ilex ecosystem: lesson from a throughfall exclusion experiment［J］.Journal of Hydrology，2008，357:57－66

［8］ Lu Xiangyu，Tang Kaijun.Study on rainfall interception characteristics of natural hardwood forest in central Taiwan［J］.Bulletin of Taiwan Forestry Research Institute，1995，10(4):447－457

［9］ Allen R G，Pereira L S，Raes D，et al.Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements［M］.Rome: FAO，1998:4－13

［10］Rowe L K.Rainfall interception by an evergreen beech forest，Nelson，New Zealand［J］.Journal of Hydrology，1983，66:143－158

［11］曹云，黄志刚，郑华，等.柑橘园林下穿透雨的分布特征［J］.水科学进展，2007，18(6):853－857

［12］魏天兴，朱金兆，张学培.林分蒸散耗水量测定方法述评［J］.北京林业大学学报，1999，21(3):85－91

［13］Deguchi A，Hattori S，Park H T.The influence of seasonal changes in canopy structure on interception loss:application of the revised Gash model［J］.Journal of Hydrology，2006，31:80－102

［14］陈涛.蔡家川柳沟流域分布式产流模型的构建与验证［D］.北京:北京林业大学，2008:22－27

［15］Link T E，Unsworth M，Marks D.The dynamics of rainfall interception by a seasonal temperate rainforest［J］.Agricultural and Forest Meteorology，2004，124: 171－191