利用多媒体实现知识的迁移和整合例析

　　上学期，学校教科室大力倡导师生共建学科知识结构，笔者从中受益匪浅。构建学科知识结构，就是对所学的知识重新组织和构建，通过对照比较寻找联系，将彼此分散、彼此分割开来的知识进行迁移和整合，形成一个统一的整体，从而使认知结构更加完善。现就本人在利用多媒体实现知识的迁移和整合的一点做法举例说明。
　　定理：一个角的两边和另一个角的两边分别平行时，这两个角相等或互补。
　　这是初中数学中的一个正确命题，可当成定理使用，它把平行线性质的3条定理和平角的定义及“对顶角相等”定理统一起来，联成一体。我们可以借助多媒体进行形象直观的演示，让学生理解记忆并应用。
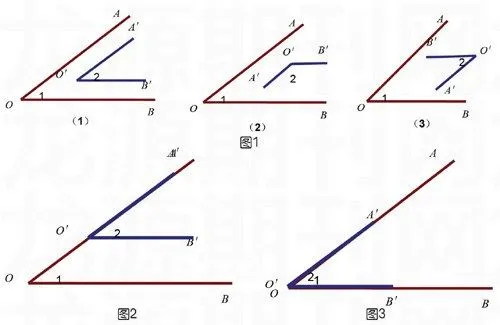
　　上面的定理包含下面3种情况（如图1所示）。
　　在情况（1）和（3）中，∠1=∠2；在情况（2）中，∠1+∠2=180°；
　　3种情况，都是O′A′∥OA，O′B′∥
　　OB。在情况（1）里，当O′A′边所在直线向左平移和OA边所在直线重合时，恰恰是“平行线的性质定理1：两直线平行，同位角相等”（如图2所示）。
　　在这里，这个定理成为了“平行性质定理1”的推广，而后者则是前者的特例。
　　同样，在情况（2）和（3）里，当O′A′边所在直线向左平移和OA边所在直线重合时，定理就变成了平行线性质定理2和定理3。即“两直线平行则同旁内角互补”和“两直线平行则内错角相等”。
　　
　　这样一来，这个定理便囊括了平行线性质的3条定理，平行线性质的3个定理不过是这定理的3种特殊情况；在课本中，先学习平行线性质的3条定理，再到后来学习这个“定理”，并且是用平行线性质定理推导证明出这个“定理”。这个先后顺序，又恰恰是我们认识世界和科学发展的一般规律：从特殊到一般。
　　当学生的认知结构达到这种自觉程度之后，再使学生回过头来审视，平行线性质的3条定理是不是也有渊源呢？它们是不是也是某些特殊情况的推广呢？
　　继续运用多媒体演示，在图2中，把∠A′O ′B ′沿AO平移，使O′和点O重合，到图3时，这正是所讲的“角重合的定义”。
　　如果把刚才的演示倒过来，我们发现：平行线性质定理1“两直线平行，则同位角相等”成为了“角重合定义”的推广，而后者则是前者的特例。
　　同样，平行线的性质2“两直线平行，则同旁内角互补”成为了“平角定义”的推广；平行线的性质3“两直线平行，则内错角相等”成为了“对顶角相等”定理的推广，而后者则又都是前者的特例。
　　这样一来，又出现了和前面的总结完全相同的情形：平行线性质3条定理，包括了“角重合（相等）定义”、“平角定义”、“对顶角相等”定理，是它们的推广；而这两个定义和一个定理，不过是平行线性质3条定理的特例。
　　综观以上两个阶段的从特殊到一般的演示，是站在系统的角度，运用“运动”的思想（平移∠A′O′B′使得O′A′到OA边所在的直线上，又使O′B′到OB边所在直线上），寻找到定理和它以外的事物的联系，完成了使这总共7个定理、定义浑然一体的伟业，实现了知识越多反而越少的追求，学习了从特殊到一般，再从一般到特殊这样一个重要的思想方法。
　　根据这个发现，当我再教到这里时，我就能够利用信息技术引导学生跨年级和章节进行知识整合，解决2个定义和5个定理的问题，让学生真正明白知识的来龙去脉以及知识间的内在联系，形成新的认知结构，实现知识的迁移。这样，不但有利于巩固已学得的知识、技能和概念，而且还有利于培养学生举一反三、触类旁通的学习能力和探索发现能力；老师的课堂也做到了马新兰教授所说的那样：“新课不新，旧课不旧”。