海岸线长度量算方法的研究
刘春杉,王华接,沈亮
( 广东省海洋与渔业环境监测中心,广东 广州 510222 )
海岸线长度量算方法的研究
刘春杉,王华接,沈亮
( 广东省海洋与渔业环境监测中心,广东 广州 510222 )
海岸线是重要而宝贵的自然资源,准确量算海岸线长度是摸清海洋家底和实施有效管理的前提。但目前海洋界没有统一的海岸线长度量算方法。提出基于高斯平均引数的椭球面长度算法,并采用MapBasic语言的实现海岸线长度的自动化计算,通过验证和比对,比目前海洋界普遍采用的平面长度算法更准确,可在实际工作中推广。
海岸线;椭球面长度算法;高斯平均引数
1 背 景
海岸线是重要而宝贵的战略资源,既是港口、旅游、养殖等海洋产业发展重要载体,也是海洋生态多样性重要的来源,具有一定的稀缺性和不可再生性质。通过对海岸线的有效管理,合理利用海岸线,并使其发挥最大的社会经济效益,对于当前面临经济结构调整和产业结构升级的广东省来说,具有重要的现实意义。
海岸线位置和长度是海洋综合管理的重要基础数据,准确计算海岸线长度,是摸清海洋资源家底和实现对海岸有效管理的前提。近年来,受自然和人为因素的影响,海岸线变化较大,20世纪 80年代进行的“全国海岸带和海涂资源综合调查”中的海岸线数据资料已不能反映当前我国海岸线的现状,不宜再作为现实管理和规划制订的依据,有必要重新测量海岸线位置并计算其长度。2003年起,国家海洋局启动了“我国近海海洋综合调查与评价专项”(简称“908”专项),专项要求对海岸线重新做了修测,测量最新的海岸线位置并计算其长度。
与以往大规模调查不同,本次海岸线修测基于WGS84坐标系,采用GPS实测与遥感影像提取相结合的先进技术手段,对于可以到达的海岸,顺直海岸每隔50 m定一个点,曲折海岸适当加密,采用 RTK-GPS实测海岸线;对于难以到达的海岸,则采用 1︰10000比例尺地形图矢量化后的数据与2005年的SPOT遥感影像数据叠加拟合、修正、提取海岸线。最终两者通过GIS系统拼接合并成为完整而连续的海岸线矢量数据。
应该说明的是,海岸线的长度没有一个公认的准确测量方法。按照分形理论,采用不同的测量精度,设置不同的步长,所得出的海岸线长度值都不相同,理论上海岸线可以无限长。本文所讨论的内容是选择更准确的算法,对已经测量好,并采用计算机存贮的海岸线矢量数据进行长度计算。
2 问题的提出
传统的地图上曲线长度的量算包括两脚规法、曲线计法、贴铜丝法等,都是在图纸上借用相应的设备进行手工量算,受图纸的保存程度、比例尺、投影以及手工操作误差影响较大。目前,地图、测绘等领域都进入了数字时代,地图上的曲线如海岸线等都是按照节点顺序,以节点坐标的形式贮存在计算机中,通常称之为矢量数据,而地图上曲线长度量算已转化为对曲线矢量数据的长度量算。
海岸线矢量数据能够准确的描述海岸线的位置,但其长度值却有多种量算方法,不同的方法可以得出不同的长度值。在此次海岸线修测中,国家制订了《海岸线修测技术规程》,规程中提出:“在1︰50 000专题图上进行海岸线长度量算”、“图件的坐标系采用 WGS-84,高斯-克吕格投影”,但规程并未提出具体的长度量算方法。
目前,我国海洋管理部门和海洋研究部门多采用高斯-克里格投影下的平面长度算法来计算海岸线长度。这种算法存在缺陷,在短距离、小范围情况下使用时误差不大,但对于“成千上万”公里的海岸线来说,累积误差过大。今后应采用更接近实际长度的椭球面长度算法,来计算海岸线长度。
3 量算方法的比选

图 1 地球椭球体Fig. 1 Earth ellipsoid
为了测量成果的计算和制图工作的需要,通常选用一个同大地体相近的,可以用数学方法来表达的旋转椭球体来代替地球。这个旋转椭球是一个椭球绕其短轴旋转而成,其表面成为旋转椭球面。
如图 1所示,地心距赤道的距离为长半轴(a=OA),地心距南北极点(S、N)的距离为短半轴(b=ON),每一个纬圈都为圆,每一个经圈都为椭圆(a为长半轴,b为短半轴)。
海岸线可以看作是附着在地球表面的曲线,对于这种曲线的长度,可以两种类型的量算方式,一种是椭球面按一定算法投影到平面上,然后计算节点间的平面距离并累积而求得曲线长度,简称为平面长度算法,另一种是不经投影,直接从地球表面计算节点间的距离并累积求得曲线长度,简称为椭球面长度算法。
3.1 高斯-克里格投影下的平面长度算法
高斯投影是普遍应用于大、中比例尺的地形图制图的一种投影,也是海岸线修测规程所要求的成图投影。高斯投影下的平面长度算法为先计算相邻节点间的平面距离,再对曲线中所有相邻节点距离进行累加,得出曲线长度。计算公式为:

S:曲线线段长度
Si:相邻节点间连线长度
Xi,Yi:节点横轴和纵轴平面坐标值
作为等角投影的一种,高斯投影存在长度变形的情况,变形公式为:
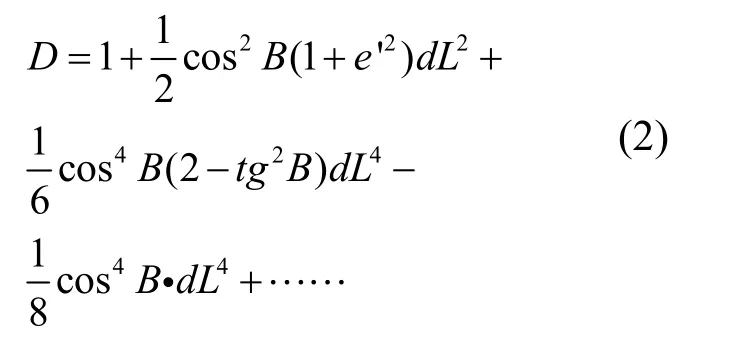
D为变形比,e’为地球的第二偏心率,B为纬度,dL为距中央经线的经度差。
从公式可知,即在东西方向上,距中央经线越远,长度变形越大,中央经线上无变形;在南北方向上,离赤道越近,变形越大,南北两极无变形。
广东省位于低纬度地区,东西跨度超过 8°。按照高斯投影6°分带,全省沿海分属两个投影带,按照3°分带,则全省沿海分属3个投影带。故若按照高斯投影下的平面长度量算方法,则广东省的海岸线长度的累计误差较大。
3.2 椭球面长度算法
与平面长度算法相同,椭球面长度算法也分为2步,即先计算相邻节点间距离,再对所有相邻节点间的距离进行累加。
椭球面上2点间的距离可以有不同的算法,可以计算过2点的大圆劣弧长度,可以计算2点间的法截弧长度,也可以计算2点间的大地线长度。
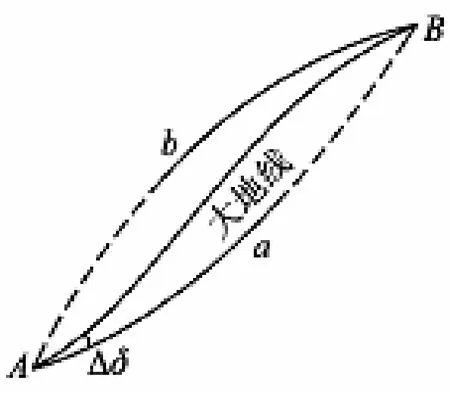
图 2 大地线Fig. 2 Geodesic
按照大地测量学,椭球面上两点间的最短程曲线叫做大地线(又称测地线,如图 2所示)。本文所述的椭球面长度算法,即通过计算海岸线上所有相邻节点间的大地线长度,再累加得出曲线长度。采用椭球面长度算法有3大好处:
第一,由于大地线是两点间惟一最短线,因此由相邻节点间大地线累计的曲线长度更为准确;
第二,由于大地线的长度值取决于两点的经纬度和椭球体的长、短半轴,与投影无关,可以保证曲线在不同投影下长度值的一致性;
第三,对于经度跨度大的曲线来说,采用椭球面长度算法,算法更为简单,可以避免平面长度算法中因跨带而需要将完整的曲线分解成不同投影带的线段,并变换中央经线等参数才能较为准确计算的麻烦。
通过已知2点,计算两点间的大地线长度称为大地主题反算(与大地主题正算合起来统称大地主题解算)。据不完全统计,大地主题解算方法有 70多种,其中适用于短距离的量算的有高斯平均引数法,适用于中长距离量算的有贝塞尔公式以及由它派生的公式,考虑到本次海岸线相邻节点间距离一般不超过1 km,而高斯平均引数法解算公式结构虽然复杂,但精度比较高,反算无需迭代,方便计算机编程,因此本文采用高斯平均引数法进行大地主题反算。
4 椭球面长度算法的实现
4.1 相邻节点距离量算
假设地球表面有两点P1,P2(如图3所示),设 S 为 P1,P2两点间大地线长度,(L1,B1),(L2,B2)分别为2点的经纬度坐标。
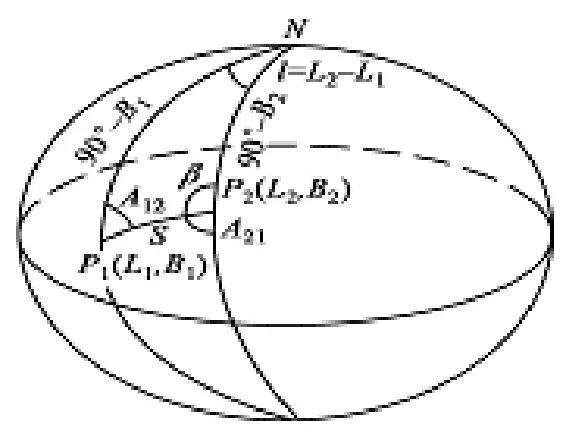
图 3 椭球面长度Fig. 3 Ellipsoid-Length
按照高斯平均引数正算公式,可推导出高斯平均引数反算公式3:


其中 a,b分别为椭球体的长半轴和短半轴。其值采用WGS84椭球体的参数。
最后,由三角函数可得公式5:
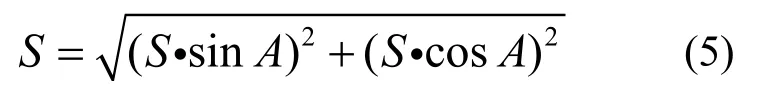
将公式4代入到公式5即可计算两点间的大地线长。
为方便海岸线长度的量算,作者采用了可直接读取海岸线各节点坐标值的MapBasic7.0(MapInfo的附属开发包)编程实现曲线长度的自动化计算。代码主要包括两点间的距离量算和曲线中各节点间距离的累计。
两点间的距离量算核心代码为:


4.2 曲线长度计算
在曲线中按顺序将节点历遍,计算相邻两节点间的距离(大地线长),并且累加。
核心代码为:

5 验 证
在地球椭球面上,赤道圈为大圆,半径为地球长半轴,子午圈为椭圆,长、短半轴与地球的长、短半轴一致。按照大地测量理论,赤道线上任意 2点间的球面距离为这两点间的赤道劣弧长,同样子午线上任意2点间的球面距离为2点间的子午劣弧长。由于子午圈弧长和赤道弧长都有现成的精确计算公式,可求取准确长度,因此在子午圈和赤道上各截取2段曲线作为椭球面长度算法和平面长度算法的验证。
由对照表1可知,采用公式4、5所得出的地球表面曲线长度是准确的,算法是可信的。

表 1 子午弧长和赤道弧长验证结果对照表(单位:m)Tab. 1 Results table of latitude and equatorial arc length (unit: m)
6 算 例
如图4所示,曲线AE为广东、香港、澳门的大陆海岸线,西至109.685°E,东至117.191°E。用 112.5°E、114°E、115.5°E 3条经线与曲线AE相交,分别得到B、C、D 3个交点。
按照高斯投影6°分带,广东沿海位于19、20两个投影带,其中曲线AC位于19投影带,中央经线为111°E;曲线CE位于20投影带,中央经线为117°E。
按照高斯投影3°分带,广东沿海位于37、38、39三个投影带,其中曲线AB位于37投影带,中央经线为111°E;曲线BD位于38投影带,中央经线为114°E;曲线DE位于39投影带,中央经线为117°E。
按照平面长度算法和椭球面长度算法,分别对曲线AE、AC、CE、AB、BD、DE进行长度测量,对照结果见表2。
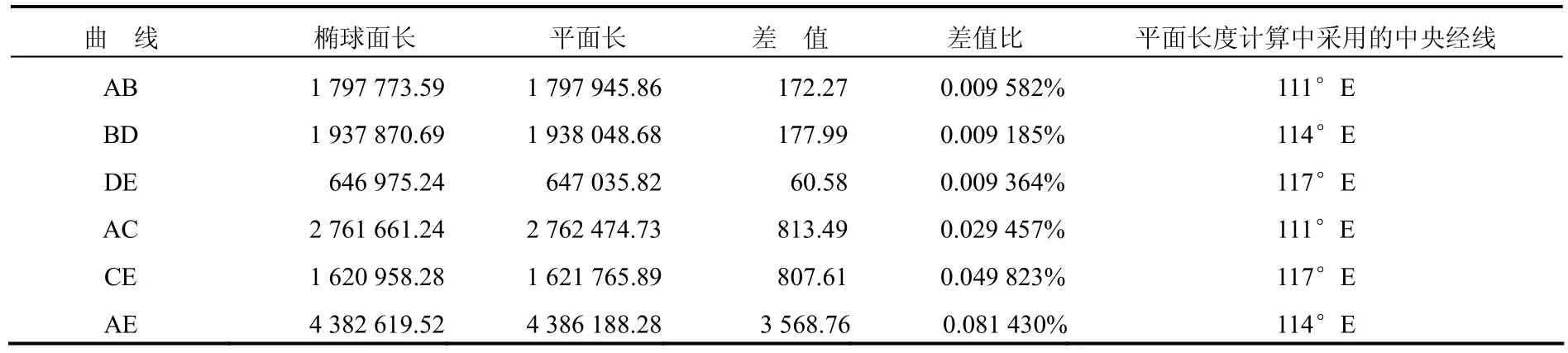
表 2 椭球面长度与平面长度计算结果对照表(单位:m)Tab. 2 Result comparison of ellipsoid-length and plane-length (unit: m)
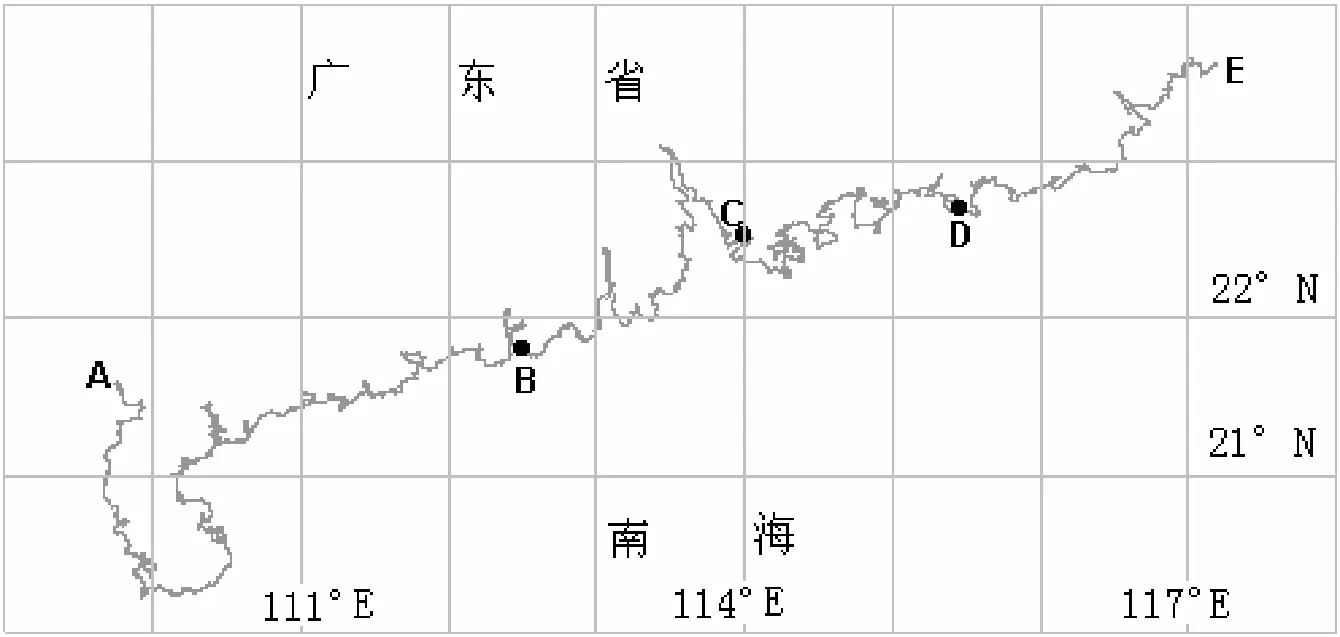
图 4 广东省海岸线示意图Fig. 4 Guangdong coastline
对照结果表明:采用平面长度算法与椭球面长度算法差别并不大,当海岸线长度较短时,两者算法所得结果相近;但当量算对象长度足够长时(如广东省海岸线超过4 000 km),平面长度算法与椭球面长度算法所得出的结果误差绝对值较大。
7 结 论
从验证和算例的结果来看,本文推荐采用的基于高斯平均引数算法的椭球面长度计算方法理论是合理的,算法是可信的,比平面长度算法结果更准确,可在今后海岸线长度量算工作中推广应用。
[1] 孔详元. 大地测量学基础 [M]. 武汉: 武汉大学出版社, 1996:30-45.
[2] 张力果. 地图学(第二版)[M]. 北京: 高等教育出版社, 1991:56-73.
[3] Benoît Mandelbrot. How Long Is the Coast of Britain? [J]. Science,1967, 156(3775): 636-638.
[4] 李炳亚. 滩涂面积及海岸线长度计算方法 [J]. 遥感信息, 1987, 2:34-36.
[5] 周振宇, 郭广礼, 贾新果. 大地主题解算方法综述 [J]. 测绘科学, 2007, 32(4): 190-191.
[6] 赵长胜. 高斯平均引数计算大地坐标主题反解的迭代算法 [J].测绘通报, 2004, 10: 11-12.
[7] 丁佳波. 海图上计算海岸线长度和海区面积的投影计算方法 [J].地图, 1996, 02: 67-68.
[8] 林桂兰, 郑勇玲. 海岸线修测的若干技术问题探讨 [J]. 海洋开发与管理, 2008, 7: 61-67.
[9] 刘仁钊, 伍吉仓. 任意精度的子午线弧长递归计算 [J]. 大地测量与地球动力学, 2007, 27(5): 59-62.
[10] 严伯铎. 椭球子午线弧长的一种计算方法 [J]. 地矿测绘, 2003,19(3): 7-10.
Study on the coastline length calculation methods
LIU Chun-shan, WANG Hua-jie, SHEN Liang
(Guangdong Ocean and Fishery Environment Monitoring Center, Guangzhou 510222, China)
Coastline is the important and valuable natural resource, and accurate calculation of the coastline length is the premise of understanding the status of marine resources, and effective management of coast. But there is no uniform method of calculating the length of the coastline. This paper proposes using Ellipsoid-Length algorithm based on Gauss mid-latitude formula to calculate the length of the Earth's surface curves, and running MapBasic programming to automatically get the length. Through the verification and comparison, the results show that Ellipsoid-length algorithm is more accurate than Plane-Length algorithm, and worth the promotion in future work.
coastline; Ellipsoid-Length algorithm; Gauss mid-latitude formula
P229.2
A
1001-6932(2011)05-0481-06
2010-07-15;
2010-08-25
我国近海海洋综合调查与评价专项(908专项)。
刘春杉 ( 1976-),男,工程师,主要从事海洋测量和信息化建设。电子邮箱:lcs158@gmail.com。

