基于PWB-EMT的电磁效应评估方法与软件实现
赵 翔,张华彬,刘 娟,黄卡玛
(四川大学电子信息学院,四川成都 610064)
基于PWB-EMT的电磁效应评估方法与软件实现
赵 翔,张华彬,刘 娟,黄卡玛
(四川大学电子信息学院,四川成都 610064)
PWB方法的网络化公式是以电磁拓扑学和统计电磁学为基础而发展起来的一种电大尺寸系统电磁效应的系统级评估方法。本文将PWB方法的网络化公式发展为更具有一般性的一套分析方法,并介绍自主开发的以该方法为基础的自动分析软件。
电磁拓扑学;统计电磁学;功率平衡法;自动分析软件
外部电磁干扰对电子系统的作用效应评估,对于电磁兼容和电子对抗等领域具有重要的研究和应用价值。传统全波分析技术很难成为电子系统(特别是电大尺寸系统)电磁效应的系统级评估方法。原因之一是,全波分析技术建立在对系统结构进行精细的几何网格划分的基础上,这就带来了计算空间和时间上的巨大代价,很多时候已经超越了目前的计算能力。原因之二是:既便有能力进行全波分析,但电大尺寸系统的电磁响应具有很高的敏感性,几何结构的微小变化会导致场分布的巨大变化。这种情况在腔体中尤甚,其中一台装置或一根电缆的位置变化都会引起场局部最小值和最大值的变化。由于实际情况中电大尺寸系统的几何结构和外部电磁干扰等不可能完全精确地被描述,确定性的计算结果可能和实际情况相去甚远。因此这样的响应敏感性使得理论上的确定性问题变成了实际上的不确定性问题,即随机性问题,有必要使用概率统计的方法求解。此外,还存在如电子系统天线朝向、系统摆放姿态、电缆姿态以及系统工作状态等若干不确定性因素。HOLLAND等指出[1],“即使有超级计算机和最好的FDTD或FVTD代码可用,也可以断言确定性解没有什么价值,因为系统一旦有1°的倾斜或频率有1%的偏移就会造成导线或电路装置上的激励有20 dB的变化”。
为了研究电磁脉冲对复杂电子系统的干扰,上世纪七、八十年代国外研究者从电磁脉冲加固研究中提出了电磁拓扑学(Electromagnetic Topology,EMT)的概念,其目的在于提出一种形式化的电子系统分析和设计方法,使电子系统能抵御各种电磁干扰[2-3]。随后,BAUM等人从多导体传输线网络(MTLN)分析中提出BLT方程[4],该方程可以视为对微波网络理论的推广,可以用来描述由电磁拓扑学构建的拓扑网络中电磁能量的传播。结合了BLT方程之后,电磁拓扑学则真正从一组概念深化为一套较完备的理论。不同于较为“笨重”的全波分析方法,电磁拓扑学理论和BLT方程的建立,为实现对大目标的建模和电磁耦合分析开辟了一条新的道路。随后,PARMANTIER成功地将BLT方程进行计算机编码实现,以此开发了一套计算软件——CRIPTE[5]。PARMANTIER提出了一套低频计算策略,在电磁拓扑学的框架下把特定的电磁计算工具完成的较简单的计算联结起来,但他同时也指出电大尺寸系统的响应(即高频耦合问题)具有很高的敏感性,如何处理这种情况是一个具有挑战性的课题[6]。
其实,已有不少研究者在研究腔体的高频响应问题时,早就发现了响应敏感性问题,并且采用了概率统计方法来研究该问题[7]。1994年Hill等首次提出功率平衡(Po Wer Balance,PWB)方法,用于求解腔体的高频响应问题[8]。该方法基于概率统计学概念,认为当腔体尺寸远大于波长时,腔体内的电磁场量是随机变量。1999年HOLLAND等出版《统计电磁学》一书[1],该书从概率统计学的角度描述在内部驱动或外部入射场激励(有泄漏)的情况下封闭腔内的电磁场(或功率流密度)的概率分布和局部自相关性。
电磁拓扑学和统计电磁学一直相互平行地发展,直到2005年JUNQUA等将电磁拓扑学和PWB方法结合起来,导出PWB方法的网络化公式,用于估算由多腔体构成的系统在外部高频干扰下所感应的电磁能量的量级[9]。该方法包含了若干随机因素,如腔体中设备的准确位置和电缆的走线情况等未知。本文将JUNQUA等人的方法发展为更具有一般性的一套分析方法,并介绍自主开发的以该方法为基础的自动分析软件。
1 基于PWB-EMT的电磁效应评估方法
根据EMT和PWB方法,将拓扑图中的节点分为3类。
1)理想节点:代表某个腔体,通常为多端口节点,各端口对应不同的能量损耗机制。根据PWB法则,对于图1a)所示的理想节点i,可得分别为节点i相对于节点jk的平均耗散功率和平均功率密度。显然,若该节点的度为n,则由该节点可以构造出n个方程。
2)能量损耗节点:代表系统的某种实际损耗,通常为单端口节点。对于能量损耗节点i,有σiSi=Pi,其中P表示其平均耗散功率,S表示对应腔体的平均功率密度,σ表示平均耦合截面,参量σ是需要被确定的。一个损耗节点可以构造出一个方程。
3)能量耦合节点:代表两腔体间的能量耦合关系,通常为双端口节点。对于如图1b)所示的能量耦合节点i,有,其中σ为该耦合关系对应的耦合截面。一个耦合节点可以构造出两个方程。
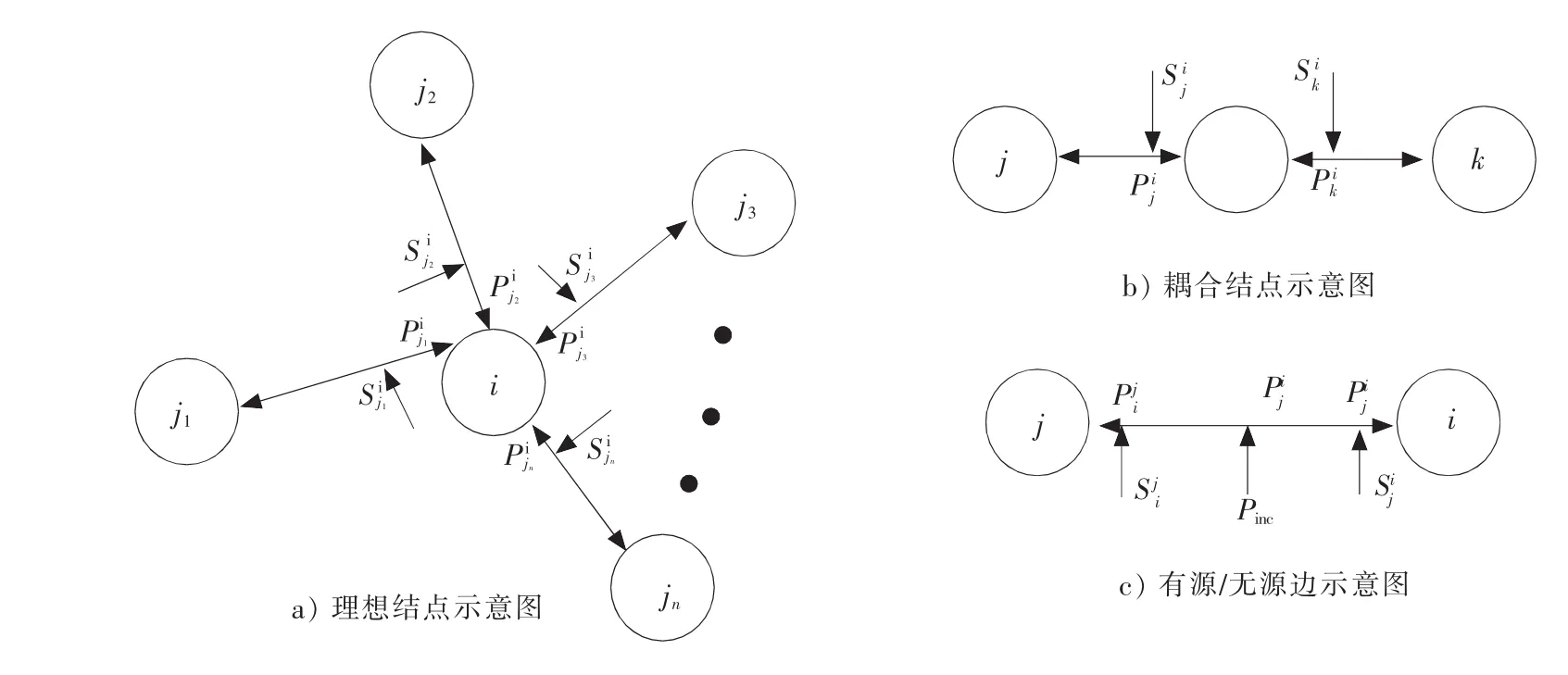
图1 理想节点、耦合节点和有源/无源边示意图
另一方面,拓扑图中的边又可分为普通(无源)边和有源边。对于如图1c)所示的有源边(Pinc≠0)或无源边(Pinc=0),有。显然一条边可以构造出两个方程。上述方程中的能量耦合截面对应腔体的不同能量损耗机制,例如入射、接收天线的损耗、腔体壁的热损耗、孔缝耦合带来的损耗等。各种机制带来的能量损耗大小均可折算成不同大小的平均能量耦合截面〈σ〉。例如:对于天线的损耗,有〈σout〉=λ2(1-|S11|2)/8π,其中S11为天线在自由空间的反射系数。对于腔壁损耗,有中μr,σ,S分别表示腔壁的相对磁导率、电导率和内表面积。可以证明,按上述方法构建出的方程总数和未知量个数正好匹配,于是,通过求解由上述方程共同构成的线性代数方程组,就可以确定全部未知量。
2 PWB-EMT自动分析软件
基于上述方法,采用面向对象的设计方法开发了PWBEMT(1.0版)自动分析程序(见图2)。
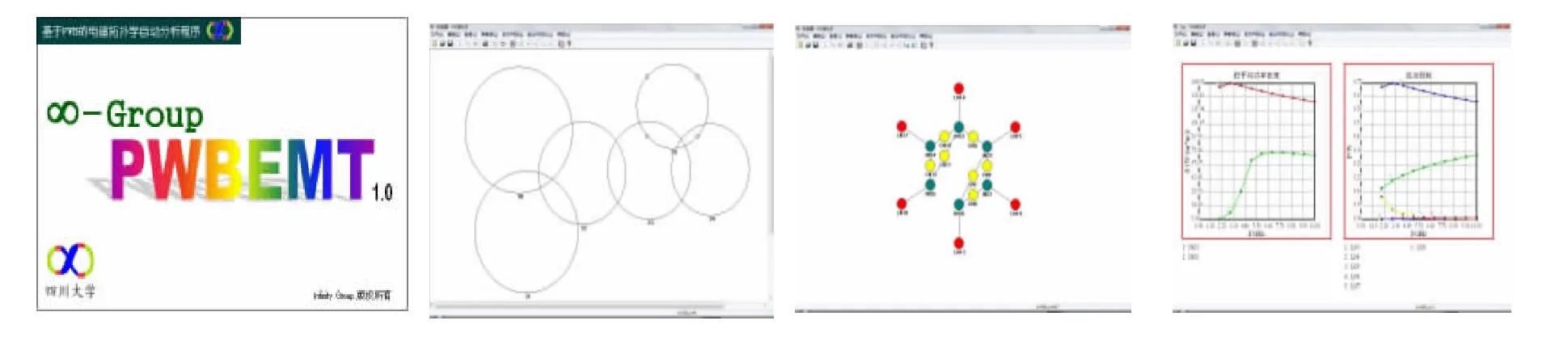
图2 PWBEMT(1.0版)自动分析程序的部分程序界面
图3给出了使用PWBEMT软件对一实际电大的多腔体系统(1 000 mm×450 mm×1 000 mm)进行电磁能量耦合分析的实例(在普通PC机上分析时间约2 s)。分析获得了1~20 GHz频率范围内端口间的S参数,并和由矢量网络分析仪测得的结果进行对比。对比结果表明PWB方法能获得和测试结果变化趋势较为一致的分析数据,能以较全波分析小得多的计算代价对电磁能量耦合情况做数量级上的分析。
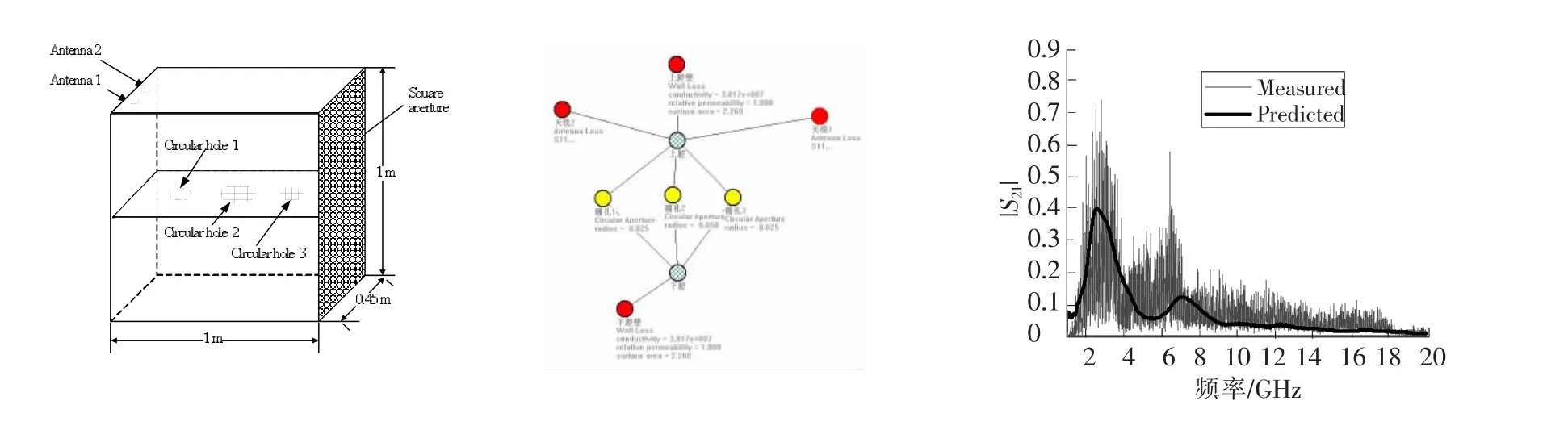
图3 PWBEMT分析结果与实验结果对比
3 结 语
PWB方法的网络化公式是以电磁拓扑学和统计电磁学为基础而发展起来的一种电大尺寸系统电磁效应的系统级评估方法。本文将PWB方法的网络化公式发展为更具有一般性的一套分析方法,并介绍了自主开发的以该方法为基础的自动分析软件和一个分析实例。
[1] HOLLAND R,JOHN R S.Statistical Electromagnetics[M].Taylor:Francis Press,1999.
[2] TESCHE F M.Topological concepts for internal EMP interaction[J].IEEE Trans Antennas Propagat,1978,26:60-64.
[3] LEE K S H.EMP Interaction:Principles,Techniques and Reference Data[M].Washington:Hemisphere Press,1986.
[4] BAUM C E.Modern Radio Science[M].London:Oxford Univ Press,1990.87-101.
[5] PARMANTIER J P,DEGAUQUE P.Topology based modeling of very large systems,Modern Radio Science[J].J Hamelin,1996(1):151-177.
[6] PARMANTIER J P.Numerical coupling models for complex systems and results[J].IEEE Trans Electromagn Compat,2004,46(3):359-367.
[7] KOSTAS J G,BOVERIE B.Statistical model for a mode-stirred chamber[J].IEEE Trans Electromagn Compat,1991,33(4):366-370.
[8] HILL D A,MA M T,ONDREJKA A R,et al.Aperture excitation of electrically large lossy cavities[J].IEEE Trans Electromagn Compat,1994,36(3):169-179.
[9] JUNQUA I,PARMANTIER J P,ISSAC F.A Network formulation of the power balance method for high-frequency coupling[J].Electromagnetics,2005,25:603-622.
O451
A
1008-1542(2011)12-0165-03
2011-06-20;责任编辑:王士忠
国家自然科学基金青年基金项目(60801035)
赵 翔(1973-),女,四川名山人,副教授,博士,主要从事计算电磁学、电磁效应评估方面的研究。

