描述结构动力卸载刚度的指标验证

林煌斌，王全凤

（1.华侨大学 土木工程学院，福建 泉州361021；2.同济大学 航空航天与力学学院，上海200092；3.集美大学 工程技术学院，福建 厦门 361021）

描述结构动力卸载刚度的指标验证

林煌斌1，2，3，王全凤1

（1.华侨大学 土木工程学院，福建 泉州361021；2.同济大学 航空航天与力学学院，上海200092；3.集美大学 工程技术学院，福建 厦门 361021）

提出可用于描述结构动力卸载刚度修正系数和能量变换关系系数，建立卸载过程的弹性变形能及卸载刚度表达式，并用钢骨混凝土柱恢复力试验数据对结论进行可行性验证 .研究结果表明：对于在评价结构弹塑性时程分析中引入结构卸载刚度修正系数和能量变换关系系数，可以定量评价结构动力卸载，较好地解释卸载时，结构卸载刚度矩阵随时间变化构成的时变参数系统；弥补结构弹塑性时程分析中未考虑的卸载刚度与运动状态的相互影响效应，解决结构切线刚度和割线刚度表示的动力方程不等效的问题.

描述指标；卸载刚度；混凝土结构；恢复力模型；弹性变形能

刚度退化模型的刚度变化不连续，存在着拐点或突变点，但刚度计算比较简单，工程应用上常用刚度退化二线型模型、刚度退化三线型模型、刚度退化四线型模型等.刚度退化三线型（DT3）模型是用三折线表示正反向加载恢复力骨架曲线，并考虑钢筋混凝土结构或构件刚度退化性质，可更细致地描述钢筋混凝土构件的真实恢复力曲线.根据是否考虑结构或构件屈服后的硬化状况，刚度退化三线型模型分为坡顶退化三线型模型和平顶退化三线型模型［1-3］.结构系统工作时，经常是在加载过程中伴随着卸载的发生，除了加载对系统产生作用效应，也经常伴随着卸载产生的作用效应.结构系统的加载作用与卸载作用往往相互影响，使结构系统的变形和运动呈现出复杂的非线性［4-5］.结构振动中卸载时，结构卸载刚度矩阵随时间变化构成时变参数系统.目前，结构弹塑性时程分析一般未考虑卸载刚度与运动状态相互影响效应，往往造成结构切线刚度表示的动力方程和结构割线刚度表示的动力方程不等效，不能完整描述弹塑性结构振动的动力卸载过程.而且，相关文献对结构恢复力模型卸载刚度的描述缺少量化指标 .基于此，本文推导恢复力模型卸载刚度参数的确定方法并用试验给予验证.

1 动力卸载刚度弹性原则

在增量法中，单元刚度矩阵中的EI0为弹性段内的截面抗弯刚度，EI1和EI2为塑性铰区的截面抗弯刚度 .该刚度为切线刚度，可以采用条分法精确计算.截面骨架曲线确定，实际计算采用少参数近似描述骨架曲线.由于内力重分布，截面在加卸载时刚度变化，一般情况下取各转化阶段弯曲刚度，即

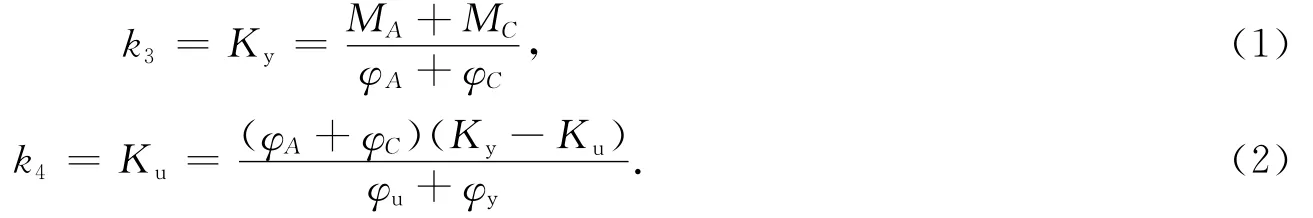
式（1），（2）中：Ku＝2.5 Mu／φu.

确定混凝土恢复力模型的卸载刚度采用以上方法，考虑其随着构件位移幅值增加而退化的因素，工程中常采用试验数据考虑轴压比、配筋率等构件物理特征进行拟合卸载刚度.

常用卸载刚度计算方法采用“卸载按弹性”的规则.在滞回过程中假定计算卸载刚度不变，实际上该过程中Ku（x）矩阵是在不断改变.变形和运动状态在匹配位置附近微小幅度波动时，可以得到稳定的计算结果 .然而，由于计算结构状态偏移，必然产生计算误差 .若变形和运动状态偏移匹配位置，则相当于计算中包含“计算扰动”量，偏移程度越大，相应的“计算扰动”也越大；若偏移程度较大或总是往某一方向偏移，则最终可能因误差积累导致出现计算不稳定.

2 结构动力卸载刚度分析

2.1 构件运动阶段

构件滞回中，弹性阶段变形不会引起结构损伤，体系能量保持守恒，不影响结构的滞回曲线.强化段结构损伤后出现刚度和强度退化损伤，结构对系统外释放能量.由于结构发生弹塑性变形后对系统外释放能量，外荷载做功不等于结构变形能，同时结构损伤导致刚度退化，形函数矩阵R保持不变，本构矩阵K相应变化.结构卸载刚度退化与结构系统能量变化有关.

文中采用的是工程应用较多的平顶退化三线型模型［1-3］，如图1所示.

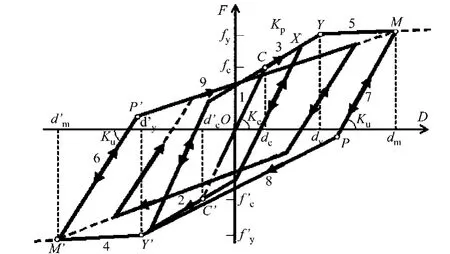
图1 刚度平顶退化三线型模型Fig.1 Trilinear model of stiffness degradation

2.2 卸载过程弹性变形能变化

（1）当滞回运动处在上升阶段（图2a），假设在CY段的X 位置卸载，OC段刚度为Ke，CY段刚度为Kp（Kp＝αKe，常数α由DT3模型确定）.

（2）当滞回运动处在下降阶段（图2b），假设在YM 段的X位置卸载，OC段刚度Ke，YM 段刚度Kd（Kd＝βKe，常数β由DT3模型确定）.

图2 卸载过程弹性变形能弹性变形能示意图Fig.2 Elastic deformation energy during unloading

当结构处于X位置，卸载过程上升段、下降段的结构累积弹性变形能分别为

式（3），（4）中：∑SR，∑SD分别为上升段、下降段的结构累积弹性变形能；Se为弹性阶段变形能，Se＝ΔOCXc；Sp为弹塑阶段的弹性变形能增量，Sp＝ΔCYX1；Sd为下降段的弹性变形能增量，Sd＝ΔYXX2；Su为卸载释放的弹性变形能，Su＝ΔXXwXx；γ为能量变换相关系数，是Se，Sp，Sd的关系参数，与材料和构件物理特征包括轴压比n0、剪跨比l／d、纵筋配筋率ρl、箍筋配筋率ρw等特征相关.

由式（4）可得能量变换相关系数的表达式为

2.3 卸载刚度修正系数

卸载刚度退化应用于表征损伤指数上，与结构损伤的演化现象相一致.构件在循环受力过程中，应变ε可分解为可逆应变εe和不可逆应变ε′，而ε′包括塑性应变εp和不可闭合损伤残余应变εu.由损伤原理可得

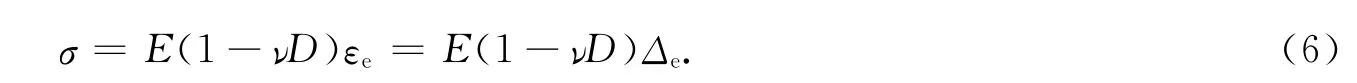
式（6）中：构件破坏时定义为D＝1，经典损伤模型D采用变形－耗能双参数组合［6］；ν为仅考虑由最大位移破坏因素的组合系数，0.5≤ν＜1.0.

由热力学内变量理论，可得含唯象损伤演化构件的力－位移比拟式为

由式（7）可知，采用卸载刚度Ku（x）描述结构损伤值D理论是可行的.

对于延性构件（2.0＜μ＜4.0），设损伤函数 D＝fd（x1，x2，…，xn）为单调递增函数，则有

卸载刚度的修正系数ξ的表达式为

式（9）中：ηi，ηi＋1分别为第i次和第i＋1次卸载刚度Kui与弹性段刚度比值 .

3 动力卸载刚度试验验证

为验证结构卸载刚度修正系数ξ和能量变换关系系数γ的指标式（5），（9），采用劲性RC柱和高强混凝土柱变形性能及恢复力特性试验［6-8］的实测数据进行验证.能量变换关系系数γ、卸载刚度Ku和卸载刚度修正系数ξ与循环次数n的关系，分别如图3～5所示.

从图3可知，在未破坏前的循环段内，γ在不同构件中的变化趋势相同，表明弹性阶段能量与卸载弹性能之间存在关系，可以通过γ（m0，l／d，ρ1，ρw）拟合.

从图4可知，各构件在循环过程中，Ku（x）的变化量呈线性单调变化，不同特征的构件卸载刚度Ku在不同循环中数值并不保持弹性原则.图3描述在滞回过程中的卸载刚度并不是保持不变的事实，但最为重要的是dKu（x）基本相等，可以用式（8）表达Kui＋1和Kui（x）的关系.

图3 能量变换关系系数与循环次数的关系Fig.3 Relationship between energy correlation coefficient and load cyclic number

图4 卸载刚度与循环次数的关系Fig.4 Relationship between unloading stiffness and load cyclic number

图5 卸载刚度修正系数与循环次数的关系 Fig.5 Relationship between unloading stiffness correction factor and load cyclic number

从图5可知，计算得到ξ值稳定保持在0.85≤ξ≤0.95区域内，可以对试验数据进行拟合得到ξ.

以上试验充分体现卸载刚度随着构件位移幅值增加而退化现象，可以解释随着实际构件偏移程度较大或总是往某一方向偏移，最终可能因误差积累导致出现计算不稳定的现象.

4 结束语

引入结构卸载刚度修正系数ξ和能量变换关系系数γ，可以更好地描述和评价结构的动力卸载现象，弥补了结构弹塑性时程分析中一般未考虑卸载刚度与运动状态相互影响所带来的不足，该结论可供结构弹塑性时程计算参考.由卸载弹性释放能量、弹性变形能增量和弹塑性阶段弹性变形能增量关系确定卸载刚度关系，可以评价钢筋混凝土结构的动力卸载，建立以刚度修正和能量变换关系的新方法，更接近描述结构构件在弹塑性时程的规律.动态调整卸载刚度是简单又实际操作意义的.

［1］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京：清华大学出版社，2005.

［2］张新培.钢筋混凝土抗震结构非线性分析［M］.北京：科学出版社，2003.

［3］吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性有限元理论与应用［M］.上海：同济大学出版社，1997.

［4］黄庆丰，王全凤.弹塑性结构动力系统的时变刚度激励效应分析［J］.土木工程学报，2006，39（12）：18－23.

［5］王全凤，黄庆丰.损伤结构弹塑性抗震性能分析及评价［J］.华侨大学学报：自然科学版，2009，30（1）：6－11.

［6］PARK Y J，ANG－ALFREDO H S.Mechanistic seismic damage model for reinforced concrete［J］.Journal of Structural Engineering，ASCE，1985，111（4）：722－739.

［6］张志伟.SRC柱变形能力及恢复力特性试验研究［D］.泉州：华侨大学，2007.

［7］林煌斌，王全凤.HRB400高强度混凝土柱抗震性能分析［J］.建筑结构学报，2008，29（S1）：36－41.

［8］林煌斌，王全凤.基于IDRAC损伤结构弹塑性时程分析与损伤评价［J］.建筑结构学报，2008，29（S1）：255－259.

Analysis and Experiment of New Indices to Describe Dynamic Unloading Rigidity of Concrete Structure

LIN Huang－bin1，2，3，WANG Quan－feng1
（1.College of Civil Engineering，Huaqiao University，Quanzhou 362021，China；2.School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China；3.College of Engineering Technology，Jimei University，Xiamen 361021，China）

Unloading stiffness coefficient and energy correlation coefficient to describe unloading stiffness of structure were presented.The expression of elastic deformation energy due to damage during unloading process was established，which was validated by the experimental data of steel reinforce concrete columns.In elastic－plastic time history analysis of concrete structure，the introduction of unloading stiffness coefficient and energy correlation coefficient is conducive to evaluate quantitively the dynamic unloading，to make up the deficiency without considerring the interacting effects between unloading stiffness and motion state，to solve the disequilibrium of dynamic equation between the tangent stiffness and secant stiffness.

description index；unloading stiffness；concrete structure；restoring－force model；elastic deformation energy

黄晓楠 英文审校：方德平）

TU 313

A

1000－5013（2011）06－0676－04

2011－10－27

林煌斌（1981－），男，讲师，主要计算机在结构工程中应用的研究.E－mail：linhuangbin＠jmu.edu.cn.

国家自然科学基金资助项目（50578066）；高等学校博士学科点专项科研基金资助项目（200803850001）；福建省自然科学基金资助项目（2011J01320）