改进的遗传算法在配电网检修计划中的应用

欧阳玲,宋 克

(1.中原工学院,郑州450007;2.国家数字交换系统工程技术研究中心,郑州450005)

改进的遗传算法在配电网检修计划中的应用

欧阳玲1,宋 克2

(1.中原工学院,郑州450007;2.国家数字交换系统工程技术研究中心,郑州450005)

为了减少供电企业停电损失费用和检修费用,同时满足多种约束条件,本文在借鉴目前配电网检修计划编制工作经验的基础上,建立了配电网检修计划优化模型.针对该模型的特点,采用改进的遗传算法求解配电网检修计划优化问题.并通过具体优化算例计算和分析,验证了本文所提出的模型和改进算法的有效性.

配电网;检修计划;优化模型;遗传算法

配电网设备检修是电力系统中一项十分重要的内容,设备检修计划安排的好坏,直接关系到电网企业和用户的利益,对电力系统乃至整个社会的安全性和经济性都有着很大的影响.因此,根据供电企业的实际需要,建立一个兼顾电网安全性和经济性的检修计划数学模型,并设计求解该模型的算法,有着重要的理论价值和现实意义.目前,配电网设备检修计划基本上还是依靠检修人员的经验人工编制而成,在人工编制计划中,存在着可靠性差、工作效率低、经济性得不到保证等问题[1].本文首先建立合适的配电网检修计划优化模型,然后提出适合于该模型的优化算法,最后通过算例验证模型和算法的有效性.

1 配电网检修计划的优化模型

1.1 检修计划优化目标

从供电公司角度出发,配电网检修计划优化目标应包括以下两个方面:一是在保证配电网安全运行的前提下,最大限度地提高供电可靠性,降低供电企业因设备检修而造成的停电损失;二是最大限度地降低因设备检修而带来的检修成本.

对检修而言,受检修技术和检修力量的限制,检修工作的持续时间我们可以认为是固定的,也就是说每台设备每次检修停电持续时间是固定的.因此,配电网供电可靠性的提高主要是通过减少因检修而造成的停电负荷量和停电次数来实现,而这两种因素直接反映了企业的停电损失.若将导致负荷停电的设备检修时间安排在负荷低谷期,即通过优化设备的检修时间就可以降低停电负荷量,也就相应地降低了停电损失.同时,保证一次停电可以解决的问题要全面解决,不允许因考虑不周而发生重复停电的问题.

检修成本主要是支付给检修工人的工资.一般情况下,节假日所支付的工资远远高于正常工作日.因此,要尽量避免将检修工作安排在节假日,以降低检修费用.

1.2 检修计划目标函数

基于此,本文建立了以降低供电企业停电损失费用和检修费用的优化目标:在保证系统安全可靠运行的同时,尽量减少停电损失费用和检修费用[2-3].其数学描述为:

式中:f1—停电损失费用,元;

f2—检修费用,元;

p—平均电价,元/kW h;

N—待检修设备总数,台;

T—检修时段总数,d;

pit—第t时段第i个设备检修所影响负荷,

MW;

uit—第t时段第i个设备的状况,取 0时,表示设备正常运行;取1时,表示设备停机检修;

cit—第t时段第i个设备的检修费用,元.

显然,这是一个多目标优化问题,并且两个目标函数求的都是最小化问题.对于求解这类多目标优化问题,本文采用权重系数法,分别给停电损失费用f1和检修费用f2赋予不同的权重,其中w1和w2的大小代表f1和f2的重要程度,它们的线性加权和即为总的目标函数.这样一来,多目标优化问题也就转化为单目标优化问题:

式中:w1—停电损失费用权重;

w2—检修费用权重.

把式(1)和(2)带入式(3),即得到总的目标函数式:

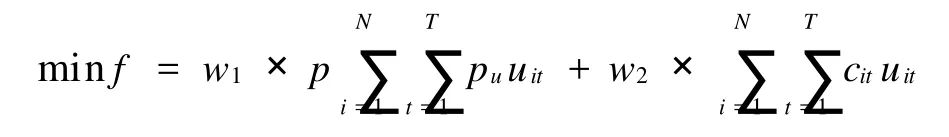
1.3 检修计划约束条件

本文的检修计划必须满足以下约束条件:

(1)同时检修约束.在一个系统中,一次停电可以解决的问题要全面解决,不允许因考虑不周而发生重复停电的问题.因此,有些设备必须同时检修.当月所有检修中,凡是使同一条线路、相同节点停电的检修,都认为是重复停电检修.在进行检修计划时间编排时,要将重复停电检修安排在相同的时间段内,即在此检修计划执行过程中只允许停电一次.

(2)互斥检修约束.为了避免负荷点在检修时停电,有些设备如互为备用的设备不能同时检修.因此不能将它们安排在相同的时间段内检修,即它们的检修时间不能有重叠.

(3)检修资源约束.检修资源是指检修人员数量及技术能力、设备能力等.由于资源有限,使得能同时进行检修的设备数量有限.

(4)检修开始时间约束.计划检修时,按主管部门颁发的全国统一的规程所规定的项目、周期进行检修安排.因此设备的检修日期有着一定的时间限制.

(5)检修持续进行.检修工作应贯彻“应修必修,修必修好”的原则,所以要保证检修工作持续进行.

(6)不可变更的检修约束.不可变更的检修包括:上级调度部门制定的检修计划;上月延续至本月的检修;事故检修等.这类检修的起始时间可认为是确定的,与之存在同时检修关系的设备检修时间也不能变更,不参加检修计划时间的编排.

(7)时间调整约束.满足下式:

式中:xoi—第i个设备申报开始检修时间,d;Ai—第i个设备调整时间限值,d.

2 改进的遗传算法

2.1 基本遗传算法的特点及缺陷

遗传算法(GA)是从自然遗传及自然选择抽象出来的寻优方法[4].与传统的优化算法如 SA、TS等相比,GA主要有全局优化、通用性强、隐含并行性、计算量大等特点.

GA的这些特点决定了它具有全局搜索能力、鲁棒性强等优点,适合解决复杂的非线性问题.因此,本文选用GA求解配电网检修计划优化问题,从理论上讲是完全可行的.

基本遗传算法(SGA)采用二进制编码、轮盘赌选择方法,交叉、变异概率取固定值.特别要注意的是:①选择采用轮盘赌方法,当群体适应度差异非常大时,最佳个体的生存机会显著增高,较差个体的生存机会被剥夺,使得最佳个体很快充满整个群体,GA较早地丧失了进化能力;②SGA中交叉概率P、变异概率Pm在整个进化过程中都取固定值(或形式不变化),这在处理复杂问题时,很难同时兼顾搜索范围广和搜索速率快的矛盾.

这就使得SGA存在一些亟待克服的缺点:①进化初期的未成熟收敛;②进化中后期由于个体竞争减弱引起的随机搜索趋势.前者导致算法收敛到局部最优解,后者导致算法的收敛缓慢.

我们知道,交叉是 GA生成新群体,带动群体进化的主要方法,是 GA的核心;变异是维持群体多样性,突破局部极值的主要手段.两种算子的操作方式对整个 GA的影响相当大.根据这一情况,本文针对具体问题改变SGA中选择、交叉、变异的操作方式,使其克服SGA固有缺陷.改进的重点主要放在:①如何增加种群的多样性以克服未成熟收敛现象;②如何提高算法的局部搜索能力以提高解的质量;③如何进行有效的搜索以提高收敛速度.

2.2 双变异率遗传算法

为了防止未成熟收敛现象,我们对基本遗传算法作出改进,采用一种双变异率遗传算法(DM GA)[5].

我们知道,为了维持种群的多样性,可以有目的地选择配对个体.一般情况下,在物种的形成过程中要考虑配对策略,以防止相似个体之间进行配对.SGA中,参与交配的个体是随机配对的,但在DM GA中,我们规定,只有当参与配对的两个个体间的广义海明距离超过一定阈值时,才允许它们进行交配.

在进化的最初阶段,由于个体间差异较大,种群相似度较小,满足条件的配对个体相对来说比较多.但随着算法的进行,尤其到了进化的中后期,个体间差异减小,种群相似度较大,这时满足条件的配对个体会随之减少,使得交叉操作产生的个体数目很有可能达不到种群规模.为此,需要引入新个体来“补充”种群规模.若采用直接随机生成的方式产生新个体,适应度值都太低,而且对算法的全局搜索性能增加并不显著.为此,我们想到在变异操作中引入双变异率(即局部小变异和全局大变异),当由广义海明距离控制的交叉操作产生的个体数不足种群规模时,说明种群中的个体有趋于相似的可能,很有可能在未来几代后陷入局部最优,此时局部变异因子发挥作用,对原种群进行小突变.这种类似于“扰动”的作用,一方面增大了搜索空间,增加了种群多样性;另一方面突变后的个体很有可能满足了配对策略,补充了种群规模.若种群规模还不够,则需反复对原种群进行局部小变异.随后的全局大变异保证了整个变异过程的全局收敛.这种对交叉、变异方式所做的改变可有效克服SGA易陷入局部最优及易发生未成熟收敛的缺点.

假设:种群规模为Size,二进制染色体串的长度为L.

定义:广义海明距离GHij是相同长度的以a为基的2个字串i和j中对应位不同基因的数量.

本文为了防止高相似个体之间的交叉操作,提出了广义海明距离阈值T.只有当种群个体间的广义海明距离GHij>T时,才可进行交叉操作.由于广义海明距离计算的是2个字串对应位不同基因的数量,因此,T=(0.1-0.3)＊L时,经实验分析得知,T的取值与种群规模、染色体长度有一定关系:一般种群规模越大,染色体长度越长,T的取值可定得略大些;反之,T的取值可定得略小些.

考虑到随着进化的进行,种群中个体间的相似度将会越来越大,尤其到了算法后期,满足配对条件的个体越来越少,需要进行多次小突变.若突变次数过多,很有可能会在算法末期将寻到的最优解破坏掉.为此,阈值T可随进化代数逐渐减少.双变异率遗传算法操作步骤如下:

步骤1:初始化群体pop,种群大小为Size;

步骤2:计算pop中个体的适应度,同时保留最优个体;

步骤3:对pop进行联赛选择操作,选择操作后的群体为TempE;

步骤4:以较大的交叉概率Pc选出一部分个体,数量记为popsize,对任意两个个体计算广义海明距离,只有当广义海明距离大于阈值T时才可进行交叉操作;

步骤5:将交叉操作产生的个体放入临时种群tempop,若tempop>Size,进入步骤 6,否则,对TempE进行局部小变异,变异概率Pm1,然后转入步骤4;

步骤6:对tempop按适应度值择优选popsize放回TempE中;

步骤7:对TempE进行全局大变异操作,变异概率Pm2;

步骤8:将步骤2中的最优个体代替TempE中的最差个体;

步骤9:将TempE赋给pop,作为下一代的初始种群;

步骤10:判断是否满足算法终止条件,即判断是否已达到最大进化代数,是则输出最终结果,否则转入步骤2.

其中,步骤5中的临时种群tempop是每一代交叉操作后的累积.

3 双变异率遗传算法配电网检修计划优化实例

对于求解配电网检修计划优化问题,采用双变异率遗传算法,流程如图1所示.

本文配电网检修计划数据选用文献[5]中某地区供电局4月份待检修设备的数据信息,如表2所示.

算例中,只有红亭1线和红琅线检修会造成负荷停电,红亭1线检修会使亭江变电所停电,红琅线检修会使琅岐变电所停电,它们所引起的停电负荷预测结果如表3所示.

分别采用 TSGA、DM GA两种方法对配电网检修计划优化问题进行求解.

图1 双变异率遗传算法检修优化求解流程图

表2 待检修设备信息

表3 停电负荷 MW

设平均电价为0.56元/kWh,本文直接用平均电价与功率的乘积来反映停电损失费用.假定检修工人在正常工作日对每台设备检修的费用为1元/d,节假日对每台设备检修的费用为3元/d,4月共30 d,其中节假日(清明节及周末)是 4、5、6、12、13、19、20、26、27日,共9天,依照这种标准来反映检修费用.

使用二进制位串编码,每一个决策变量编码码长为5位,采用二进制单点交叉,交叉概率Pc=0.8,广义海明距离阈值T=10,联赛规模为2,最优个体保留1个,局部小变异概率Pm1=0.001,全局大变异概率Pm2=0.05,权重W1=0.01,权重W2=1,种群规模为60,最大进化代数为100.

根据网络拓扑分析得到:

(1)旗河 1线、2线,北西 1线、2线,北金 1线、2线,建金1线、2线以及南鳌1线、2线是互为备用的双回路线路,所以应错开检修时间,为互斥检修关系.

(2)北金2线136开关与北金2线回路,南鳌1线133保护与南鳌1线回路同时检修.

(3)红琅线是红亭1线的一个分支,所以应在红亭1线检修的同时对红琅线进行检修.

(4)每天最多只能同时检修4个项目.

按照同时检修约束进行分组后,6号与12号可归为一组,4号与18号可归为一组,16号与17号可归为一组,即形成18组,并且本月检修计划中没有不可变更的检修约束,因此可确定这18组即为最终优化变量.

TSGA和DM GA两种算法的优化结果分别如表4和表5所示;表6为这两种算法的比较结果.

由表4-表6可以看出,两种算法都能完全避免违背各种约束条件,并且都能将引起停电损失的设备安排在最小负荷日(4月28日-4月29日)检修,使得两种算法在减小停电损失费用这一方面表现相当.但在DM GA求得的检修计划中,设备在周末检修的天数为6 d,而在 TSGA算法中,周末检修的天数为9 d,显然,TSGA的检修费用要高于DM GA.由此可以看出,用DM GA求得的检修计划更能满足实际的需要.

表4 TSGA优化结果

表5 DM GA优化结果

表6 算法比较结果

算法收敛过程如图2所示.由图2也可以看出,DM GA在收敛速度上也比 TSGA快很多,并且寻得的最优解也好于 TSGA,显示了DM GA收敛速度快、寻优能力强的特性.

图2 算法收敛过程

4 结 语

本文在分析配电网检修计划编制原则的基础上,建立了适合当前国情的配电网检修计划优化模型.同时,针对基本遗传算法存在收敛速度慢、寻优能力差、易陷入局部最优等缺点,采用一种改进的遗传算法应用于实际配电网检修计划优化中.对优化实例的分析表明,本文所提出的配电网检修计划优化模型和改进遗传算法正确、有效,具有一定的理论价值和实用价值.

[1]于尔铿,刘广一,周京阳,等.能量管理系统(EMS)[M].北京:科学出版社,1998.

[2]黄弦超,舒隽,张粒子,等.免疫禁忌混合智能优化算法在配电网检修优化中的应用[J].中国电机工程学报,2004,24(11):96-100.

[3]全宏兴,刘俊勇.电力市场下火电厂机组检修计划的研究[J].电力系统自动化,2002,26(14):35-39.

[4]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.

[5]王杰,马雁,王非.一种双变异率的改进遗传算法及其仿真研究[J].计算机工程与应用,2008,44(3):57-60.

[6]黄弦超.配电网检修计划优化方法的研究与应用[D].北京:华北电力大学,2004.

Application on Distribution Maintenance Scheduling by Improved Genetic Algorithm

OU YAN Y Ling1,SONG Ke2
(1.Zhongyuan University of Technology,Zhengzhou 450052;2.National Digital Sw itching System Engineering&Technological R&D Center,Zhengzhou 450052,China)

This paper summarizes the theo ry and achievement of maintenance scheduling p roblem,and refers the experience of maintenance scheduling work.On the basis of these analyses,a new model for distribution maintenance scheduling(DM S)w hich intends to find the most econom ical maintenance schedule w ithout violating any restrictions is p roposed in this paper.Themodel’s fitness and themethod’s validity are very co rrect by the results of a p racticalmaintenance scheduling.

distribution;maintenance scheduling;op timization model;genetic algorithm

A

10.3969/j.issn.1671-6906.2011.04.013

1671-6906(2011)04-0056-06

2011-07-15

欧阳玲(1978-),女,安徽池州人,讲师,硕士.