S波配对的超导石墨烯/石墨烯/超导石墨烯结中的近邻效应

秦志杰,李 钊

(郑州大学物理工程学院,郑州450001)

S波配对的超导石墨烯/石墨烯/超导石墨烯结中的近邻效应

秦志杰,李 钊

(郑州大学物理工程学院,郑州450001)

基于BCS理论,在紧束缚近似下,利用Bogoliubov-de Gennes(BdG)方程,通过自洽计算,研究了具有 S波配对的超导石墨烯/石墨烯/超导石墨烯结中的近邻效应.针对在超导部分和正常导体部分的费米能级匹配和不匹配两种情况,讨论了化学势对体系的局域态密度以及配对振幅的影响.研究表明,GSNS结构的近邻效应依赖于超导部分和正常部分的化学势匹配情况.

石墨烯;超导;近邻效应

石墨烯是一种具有蜂窝状晶格结构的二维电子系统,自成功制备以来,因其独特的性质,吸引了大量的来自理论和应用两个方面的研究.由于已经在一系列碳基材料[1-3]中观察到超导态,因此关于石墨烯是否存在超导电性一直受到关注[4-5].人们已经在基于石墨烯的超导/正常导体/超导(GSNS)组成的约瑟夫森结中观测到了约瑟夫森电流[6].在石墨烯晶格中,库伯对可以相干传播,这为在石墨烯中实现超导带来了希望.理论上,人们利用基于四分量的Dirac Bogoliubovde-Gennes(D BdG)方程[7]和 Bogoliubov-de-Gennes(BdG)方程来研究这一问题[8].人们对石墨烯中是否存在超导尚不清楚,但已有学者从理论角度尝试提出可能的配对机制.目前,石墨烯中的可能超导机制分为两类:一种是内禀的声子或等离子传播的超导电性[9];另一种是近邻效应导致的超导电性[10].因此,对于石磨烯中超导电性的研究,仍是值得探讨的问题.

近邻效应是指在超导体和正常导体界面附近,超导体内部的库伯对可能会渗透到正常导体一侧的某个深度内,从而在正常导体内的这一区域内诱导出接近超导体的行为.对近邻效应的研究,是超导领域实验工作者和理论工作者所关心的一个重要方面[11-12].在实验方面,测量准粒子的局域态密度(LDOS)是研究近邻效应的一个重要手段.在理论计算方面,Gorkov方程是计算接触面附近LDOS的一种有效方法[13-14].同时BdG方程因其直观的物理意义,也是考察近邻效应的另一种有效工具[15].

在本文中,我们在紧束缚近似下,利用BdG方程,研究了在 T=0 K,具有S波配对的 GSNS结构中的近邻效应.通过自洽求解,计算了在超导部分(S区)和正常导体部分(N区)的费米能级匹配和不匹配两种情况下,配对振幅以及准粒子局域态密度对于化学势的依赖关系.

1 模型与公式

为了研究 GSNS结的近邻效应,我们考虑一个二维蜂窝晶格系统,图1所示是体系的结构示意图.考虑到超导部分上格点吸引相互作用,在紧束缚近似下,体系的哈密顿可以写为如下形式[8]:

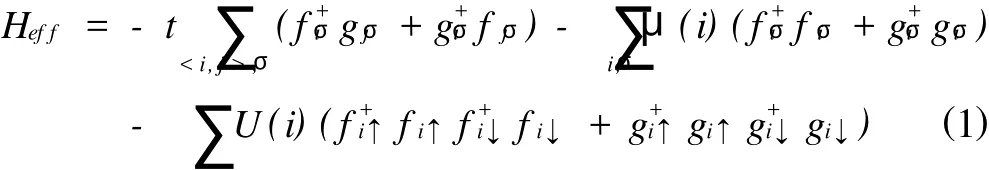
图1 GSNS结的二维晶格结构

式中:Fiσ(giσ)表示在子晶格A(B)上的i=(n,m)点处,消灭一个自旋为σ的电子;t代表跃迁积分;U(i)和μ(i)分别为在元胞i处的吸引作用强度和化学势,其中,在超导部分U(i)为一常数,在正常部分U(i)为零;表示只对最近邻的格点求和.在这里,只考虑最近邻跃迁,并取t为能量单位.由于只考虑S波配对,BdG配对势可以写为:

这里,<…>代表统计平均.计算中,配对势采用自洽计算.利用平均场近似,哈密顿量变为:

为了将BdG形式的哈密顿量对角化,对每个格点处电子的产生、湮灭算符进行如下的波戈留玻夫正则变换:

式中:N为晶格中的原胞数目;γ和γ+为新引入的准粒子产生、湮灭算符,并且满足费米子反对易关系.对角化后的哈密顿量可以写为如下形式

式中:Eg为哈密顿量的基态能量.

由以上关系,容易得到(u,v,y,z)所满足的关系:

对于有 N个原胞的晶格系统,求解上述方程的问题实际上转换为求解形状为4N×4N矩阵的本征值问题,矩阵的形式可以通过将上述方程扩展到整个晶格体系而确定下来,在绝对零度时,自洽条件(3)可以写为

为了研究近邻效应对于准粒子的局域态密度的影响,将计算并对比不同格点处准粒子的LDOS.准粒子的LDOS可通过如下公式进行计算:

在数值计算中,我们将上式中的δ函数用Lorentzian函数代替.

为了考察近邻效应,我们在此定义配对振幅为

因为配对振幅在正常区并不为零,并且它也反映了电子的配对情况,所以可以从配对振幅来考察库伯对由超导区到正常区的渗透情况.

2 计算结果与讨论

在数值计算中,按照图1中对原胞的标记方法,我们考察了大小为(N×M)的石墨烯晶格,其中 N=30,M=90.体系中的任一原胞可以用(n,m)标记,0≤n≤N-1,0≤m≤M-1.为了模拟 GSNS结构,我们沿着M方向将晶格分为3部分,首先假设晶格左边一部分(m≤29)和右边一部分(61≤m≤89)是超导体,这两部分具有相同的相互作用强度U(i)≠0;而晶格中间部分(30≤m≤60)对应正常石墨烯,这部分的相互作用强度U(i)=0,即

沿m方向我们采用开放边界条件,沿 n方向采用周期性边界条件.在此,我们感兴趣的主要是沿 m方向的LDOS和配对振幅的变化.

2.1 费米能级匹配情况

在数值计算中,首先考察超导部分的费米面和正常石墨烯部分的费米面均位于范霍夫奇点附近时的情况,即μ(S)=μ(N)=-1.04 t.图2所示为费米能级匹配的情况下,沿垂直界面方向上准粒子的LDOS随空间的分布情况.从图2可以看出,在 S区和N区接触面附近的LDOS与超导体和导体内部的情形明显不同,呈现出明显的近邻效应.在超导体内部,费米面处存在一个超导能隙,且随着格点逐渐靠近界面,这个能隙的宽度并没有大的改变,但能隙的底部随着与界面间距离的减小而逐渐上升.在正常石墨烯部分,对于远离界面的点,准粒子的LDOS具有关于狄拉克点的对称性,随着格点和界面距离的减小,费米面附近的态密度逐渐受到压制,准粒子的LDOS关于狄拉克点的对称性逐渐被破坏.在图2中,LDOS曲线并不平滑,而是出现了不同程度的震荡,这种震荡源于我们所计算的是有限体系.通常通过增加所计算体系的尺寸,LDOS在空间的震荡周期会缩短.体系非常大时,曲线最终将会趋于平滑.

图3所示为在费米能级匹配的情况下,当 S区和N区化学势取不同值的时候,沿垂直界面方向体系的配对振幅随空间的分布.从图3可以看出,在接触面附近点的配对振幅与超导体和导体内部点的不同,呈现出明显的近邻效应.在 S区,配对振幅基本上为一常数;在 N区,虽然相互作用强度为零,但配对振幅在界面附近仍然有一个小的非零值,而且在 N区随着与界面距离的增加,这个数值逐渐衰减.这反映出在超导体内部的库伯对会渗透到正常石墨烯部分,但这种渗透只发生在接触面附近很薄的一层区域.在图3中,在m=0和m=90的超导部分的边界点附近,配对振幅也出现了不同程度的震荡,这是因为所计算的体系的尺寸是有限的,加上在垂直界面的方向上采用了开放边界条件,从而导致这种情况的产生.

从图3还可以看到,当化学势μ(S1)=μ(S2)=μ(N)=-1.04 t,即费米面位于范霍夫奇点附近时,S区和N区的超导配对势振幅都具有一个比较大的值.这表明此时S区有较大的超导能隙,且此时穿透到 N区的库伯对较多.反映出当化学势取-1.04 t时,近邻效应较为明显.随着化学势对μ=-1.04 t的偏离,相应地S区的超导能隙也在减小,N区的配对振幅的大

图3 在费米能级匹配情况下沿垂直界面方向体系的配对振幅随空间的分布情况

小和穿透深度都在减小.这个结果可以根据BCS理论来理解.根据BCS理论,库伯对的配对势与费米面附近的电子态密度有关.对于石墨烯晶格,在Dirac点附近电子态密度很小,而在范霍夫奇点附近电子态密度取最大值[14],所以导致在μ=-1.04 t附近配对势的值较大.这种情况不同于正方晶格,对于正方晶格来说,S波超导配对势在化学势为零时取得最大值.因此,可以认为正是石墨烯特殊的电子结构产生了这种结果.

2.2 费米能级不匹配情况

为了研究化学势对超导石墨烯—石墨烯结的近邻效应的影响,我们进一步考察了在2个 S区化学势相同 ,但和 N区费米能级不匹配的情况,即正常区和超导区化学势取不同值的情况.图4所示为当2个 S区和N区费米能级不匹配时,沿着垂直界面方向配对振幅的空间变化曲线.

从图4(a)和(b)可以看出,当 S区化学势固定,N 区化学势μ(N)= -1.04 t时,N区的配对振幅数值最大.也就是在 S区化学势固定、N区费米面位于范霍夫奇点附近时,近邻效应最强.从图4(c)和(d)可以看出,当 N区化学势固定、S区化学势μ(S1)=μ(S2)=-1.04 t时,N区和S区的配对振幅均达到最大值.即在 N区化学势固定、S区费米面位于范霍夫奇点附近时,近邻效应最强.因此只有当 S区和N区的费米面都位于范霍夫奇点附近时,系统的近邻效应最强.结合BCS理论和石墨烯电子结构,可知这种现象是由在范霍夫奇点上二维石墨烯的电子密度达到最大值所致.

3 结 语

本文利用紧束缚模型,通过自洽求解BdG方程,研究了具有S波配对势的超导石墨烯—正常石墨烯结的性质,自洽地计算了超导石墨烯—石墨烯结在两区费米能级匹配和不匹配两种情况下,准粒子的LDOS和配对振幅随空间的变化情况.研究表明,对于具有S波配对的 GSNS结,其近邻效应对于化学势的取值有很强的依赖关系,而且这种关系和石墨烯的电子结构有关.对于石墨烯晶格,因为其特殊的晶格结构,配对势对化学势的依赖关系与正方晶格有很大的不同.我们发现,当2个S区和N区费米面都位于范霍夫奇点附近时,近邻效应最明显.这些工作将为进一步利用石墨烯作为超导电极提供一定的帮助.

[1] Weller T,Ellerby M,Saxena S,et al.Superconductivity in the Intercalated Graphite Coumpunds C6Yb and C6Ca[J].Nature Phys.,2005,1(1):39-41.

[2] Tang Z K,Zhang L,Wang N,et al.Superconductivity in 4 Angstrom Single-walled Carbon Nanotubes[J].Science,2001,292(5526):2462-2465.

[3] Gunnarsson O.Superconductivity in Fullerides[J].Rev.Mod.Phys.,1997,69(2):575-606.

[4] Beenakker C W J.Colloquium:Andreev Reflection and Klein Tunneling in Graphene[J].Rev.Mod.Phys.,2008,80(4):1337-1354.

[5] Kopnin N B,Sonin E B.BCS Superconductivity of Dirac Electrons in Graphene Layers[J].Phys.Rev.Lett.,2008,100(24):2468-2471.

[6] Heersche H B,Jarillo-Herrer P,Oostinga J B,et al.Bipolar Supercurrent in Graphene[J].Nature(London),2007,446(7131):56-59.

[7] Beenakker C W J.Specular Andreev Reflection in Graphene[J].Phys.Rev.Lett.,2007,97(6):670-676.

[8] Black-Schaffer A M,Doniach S.Self-consistent Solution for Proximity Effect and Josephson Current in Ballistic Graphene SNS Josephson Junctions[J].Phys.Rev.B,2008,78(2):0245-0252.

[9] Uchoa B,Castro Neto A H.Superconducting States of Pure and Doped Graphene[J].Phys.Rev.Lett.,2007,98(14):1468-1471.

[10] Feigel’man M V,Skvortsov M A,Tikhonov K S.Proximity-induced Superconductivity in Graphene[J].J ETP Lett.,2008,88(11):747-751.

[11] Strijkers GJ,Ji Y,Yang F Y,et al.Andreev Reflections at Metal/Superconductor Point Contacts:Measurement and Analysis[J].Phys.Rev.B,2001,63(10):1045-1050.

[12] Buzdin A I.Proximity Effects in Superconductor-ferromagnet Heterostructures[J].Rev.Mod.Phys.,2005,77(3):935-976.

[13] Belzig W,Bruder C.Local Density of States in a Dirty Normal Metal Connected to a Superconductor[J].Phys.Rev.B,1996,54(13):9443-9448.

[14] Usadel K D.Generalized Diffusion Equation for Superconducting Alloys[J].Phys.Rev.Lett.,1970,25(8):507-509.

[15] De Gennes P G..Superconductivity of Metals and Alloys[M].New York:Westview Press,1999:137-159.

Proximity Effect in a S-wave Pairing Superconducting Graphene/Graphene/Superconducting Graphene Junction

QIN Zhi-jie,LI Zhao
(Zhengzhou University,Zhengzhou 450001,China)

On the basis of self-consistent calculation of the Bogoliubov-de-Gennes equations,gate proximity effect on a superconducting graphene with S-wave pairing/graphene/superconducting grapheme junction structure is investigated.The dependence of the local density of states and pairing amplitude on the chemical potential are calculated for both the Fermi-level match case and Fermi-level mismatch case.The relation between the results and electronic structure is also discussed.Our research shows that the proximity effects in GSNS Junction depend much on the relation of chemical potentials in superconducting parts and in the normal part.

graphene;superconductivity;proximity effect

O511

A

10.3969/j.issn.1671-6906.2011.04.001

1671-6906(2011)04-0001-05

2011-07-06

国家自然科学基金项目(10874154);国家人力资源和社会保障部留学回国人员科技活动择优资助项目

秦志杰(1976-),男,河南内黄人,讲师,博士.