基于带模型的叶绿素a浓度反演精度评估

陈 军，陆 凯，王保军

(1.国土资源部海洋油气资源与环境地质重点实验室，青岛 266071;2.青岛海洋地质研究所，青岛 266071)

基于带模型的叶绿素a浓度反演精度评估

陈 军1，2，陆 凯1，2，王保军1，2

(1.国土资源部海洋油气资源与环境地质重点实验室，青岛 266071;2.青岛海洋地质研究所，青岛 266071)

为了评估遥感反演叶绿素a浓度的精度，以2004年8月19日太湖38个水质样本数据和同步Hyperion卫星遥感影像数据为基础，借鉴四波段半分析算法，结合空间数据不确定性原理，构建了基于四波段半分析算法的“带模型”。通过研究与探讨可知，当叶绿素a浓度为10～20 μg/L和50～100 μg/L时，叶绿素a浓度的反演误差较小，大约为±20%;当叶绿素a浓度在20～50 μg/L时，叶绿素a浓度的反演误差较大，大约为±40%，局部区段的误差高达±60%左右。与传统的误差表示方法相比较，“带模型”能更详细且能准确地给出太湖水体叶绿素a浓度反演结果的误差信息。

遥感;带模型;叶绿素a;太湖

0 引言

水色遥感产品(主要指叶绿素a浓度、悬浮泥沙浓度和可溶有机物质浓度遥感观测信息)的精度评估及表达是水色遥感研究的难点和热点之一。传感器辐射校正和仪器漂移等误差校正的极限值为5%，而局部误差可能更大［1－3］。在上述因素的综合作用下，35%的叶绿素a浓度反演精度已成为水色遥感技术可获取而难以跨越的精度水平［4］。在传统的水色遥感理论与应用研究的过程中，许多遥感反演水体中各种污染物质浓度的数据因缺少精度描述而被闲置［5］。加强对遥感数据及其反演产品精度的研究有助于提高遥感资源的利用率。最常用的数据精度描述方式为实测值与模型预测值之间的偏差，这种方式有利于总体上把握数据的精度信息。然而，遥感反演水体中各种污染物质浓度的精度具有时空多变性，传统的精度衡量方法适用于同步实验站点附近水域水体中各种污染物质反演精度的评估，而用于整个研究区域反演精度的描述则是不准确的［6］，甚至可能导致使用者对遥感反演水体中各种污染物质浓度数据精度的错误理解。

遥感反演数据的精度是衡量定量遥感技术发展水平的一个重要标志［7］。在模型分析和数据处理过程中，误差将从一种形式转化成另外一种形式。如果将带有误差的遥感反演数据作为空间分析算法或模型的输入参数，则将导致分析结果也具有误差［8］。在过去的数十年中，许多学者对遥感数据精度信息的表达方法做了大量而有益的探讨，并逐步形成了以“带模型”为理论核心的研究热潮［9］。ε－带模型是“带模型”的雏形，随后又出现了E－带模型，S－带模型和G－带模型等［10－12］。“带模型”是以概率统计理论为基础的，较适合于描述空间实体(如，点、线、面等)的空间位置与测量误差的关系［13］。

本研究借助于广义上的“带模型”理论，将水质参数反演函数等效地视为一条空间曲线，并将实测值与模型预测值之间的偏差视为反演函数在各个节点处的反演误差，结合2004年8月19日太湖水体中叶绿素a浓度的水样分析数据和同步Hyperion影像数据，构建了适用于叶绿素a浓度反演精度评估的“带模型”。

1 研究方法

1.1 研究数据

选取太湖作为实验区，地理坐标为E119°52'32″～120°36'10″，N30°55'40″～31°32'58″。太湖水体较浑浊，水中叶绿素a浓度(以下简称叶绿素a浓度)和可溶性有机质浓度较高，年均叶绿素a浓度约为22.23 μg/L，属于典型的Ⅱ类水体，适合开展水色遥感探测研究。

采用Hyperion影像数据及同步水质测量数据作为模型校正和检验数据。数据获取时间为2004年8月19日上午10:00。水质样本利用尼克森采水器采集于水气界面下30 cm处，同时利用手持全球定位系统(GPS)记录取样点的地理坐标。采集的水样立即放入冷藏箱中，并于当天带回实验室，先利用浓度为90%的丙酮热液萃取，然后利用荧光法来分析测量叶绿素a浓度［14］。本研究利用的光谱数据曲线是从经过数据预处理后的Hyperion影像中获取的。Hyperion数据的辐射定标、大气校正等预处理及结果评价是采用闻建光［15］等人的研究结果进行取样点位置以及从Hyperion影像中提取的水体反射光谱曲线如图1与图2所示。

图1 太湖水样采样点位置分布Fig.1 Distribution of the water samples in situ measurements in Taihu Lake

图2 从同步Hyperion影像中提取的太湖水体光谱曲线Fig.2 Spectral curves of Taihu Lake collected from the synchronous hyperion imageries

1.2 带模型

混沌理论认为，空间实体各要素之间是相互联系、相互作用的，彼此之间的作用力不平衡，进而导致了要素属性信息具有空间上的不稳定性和时间上的非周期性等特点［16］。含有观测误差的空间实体可能包含历史阶段的信息和现阶段自身发射的信息，也可能包含与其关联的实体辐射信息［17］。遥感反演水体中各种物质浓度结果的误差主要来源于影像信息采集、描述和分析过程的不确定性和水质浓度测量、分析在时间和空间上的不稳定性。影响水质浓度反演精度的主要因素包括水体光学特性的复杂程度、水体上气溶胶光学厚度的分布状况、水动力条件以及风速等因素。这些环境和天气因素在时空上具有多变性和非均匀性，以致基于局部光谱实测数据的反演算法在整个研究区域上的反演精度不高。

在平面坐标系中，假设C(x，y)是由端点A(xA，yA)和端点B(xB，yB)定义的随机线元AB上的任意一点，则点C的坐标可由点A和点B表示，即

式中，t为定比分系数，其取值范围为0≤t≤1。假设:①端点A与端点B的测量误差是不相关的，即两者的协方差等于0;②误差主要集中在叶绿素a浓度参数，而遥感参数不存在误差(对于叶绿素a浓度反演模型而言，叶绿素a浓度是依赖于遥感参数而变化的。当给定一个遥感参数，则通过反演模型即可确定与该遥感参数对应的叶绿素a的浓度。因此不妨假设遥感参数的测量是准确的，而把遥感参数的测量误差综合到叶绿素a浓度的估算误差中去，即随机线元上的任意点在x轴上的分量不存在误差，而测量误差仅存在于y分量上)。由此再对式(2)两边取方差可得

式中，D()为求方差算子。式(3)为线段AB上任意点的误差，其大小由线元端点的测量误差决定。

2 实例分析

2.1 叶绿素a浓度反演算法的带模型

［18］构建的半分析算法作为遥感反演叶绿素a浓度的反演模型，结合带模型，研究与探讨了叶绿素a浓度反演精度的估算方法。关于本文所涉及的叶绿素a浓度反演模型的构建和精度分析的详细情况可以查阅参考文献［18］。模型的估算值与实测值之间的偏差如图3所示。

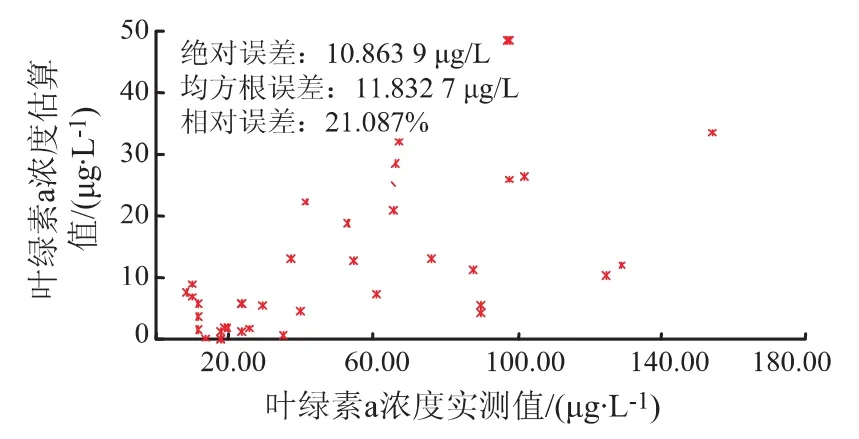
图3 四波段半分析反演算法的精度指标Fig.3 Accuracy indicators of four－ band semi－analytical algorithm

根据图3可知，四波段半分析算法的绝对误差为10.8639 μg/L，相对误差为 21.087%，均方根误差为11.8327 μg/L。将图3所示的叶绿素a浓度的各个实测数据的估算偏差代入式(3)，即可得四波段半分析算法的带模型。图4为四波段半分析算法及其“带模型”。

图4 四波段半分析反演算法及其带模型Fig.4 Band－model for four－band semi－analytical algorithm

由图4可见，四波段半分析算法的估算误差随着反演参数增加呈非规律性振荡变化，即当叶绿素a浓度在10～20 μg/L和50～100 μg/L时，叶绿素 a浓度的反演误差较小，大约为±20%;而叶绿素a浓度在20～50 μg/L时，叶绿素a浓度的反演误差较大，大约为±40%，局部区段的反演误差甚至高达±60%。太湖水体的叶绿素a浓度大体分布于20～50 μg/L，因此虽然四波段半分析算法反演结果与实测值的相关系数较高，但是对于叶绿素a浓度主要分布在20～50 μg/L的太湖水体而言，其反演精度并不理想。图3给出了四波段半分析算法反演精度的一个总体指标。当叶绿素a浓度为10～20 μg/L和50～100 μg/L时，该指标与“带模型”表达的精度信息近似一致，而当叶绿素a浓度为20～50 μg/L时，则该指标将失效。

2.2 太湖叶绿素a浓度及反演精度评估

借助于可视化交互式数据语言(IDL)二次开发平台，利用图4所示的四波段半分析算法及其带模型，从Hyperion影像中逐像元提取的叶绿素a浓度及其反演精度信息如图5所示。

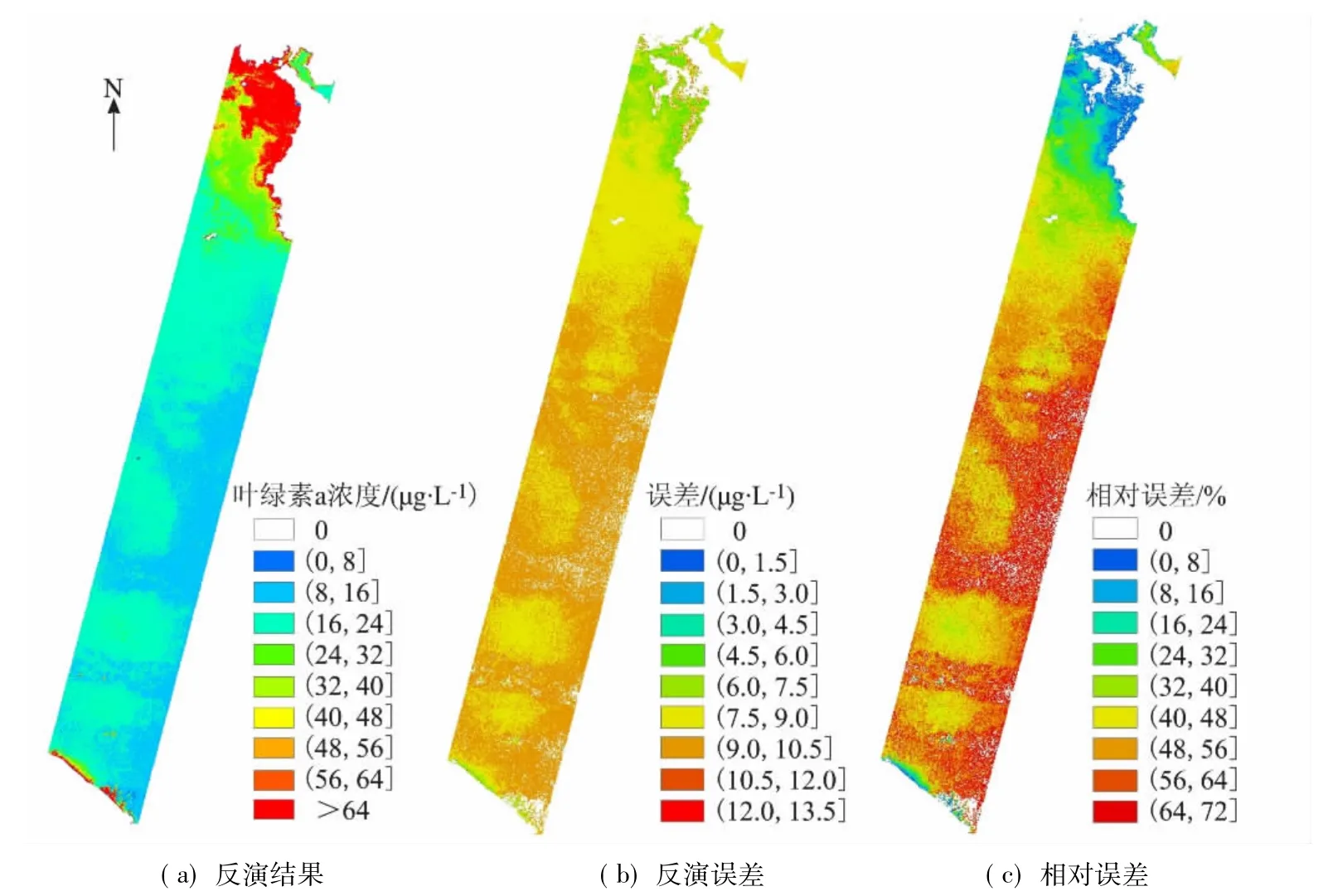
图5 太湖叶绿素a浓度及其反演精度Fig.5 Chlorophyll－ a concentration and retrieval accuracy of Taihu Lake

由图5可见，当叶绿素a浓度在10～20 μg/L和50～100 μg/L时，四波段半分析算法具有较低的反演误差，而当叶绿素a浓度在20～50 μg/L时，其反演结果的误差较高。因此四波段半分析算法反演的叶绿素a浓度的反演精度呈湖心低，湖的北部和湖的南部高的格局。另外，图5表明，四波段半分析算法对基于Hyperion影像反演的叶绿素a浓度的绝对误差不超过13.5 μg/L，其对应的相对误差为72%;大部分区域水体叶绿素a浓度的反演误差为7.5～10.5 μg/L，其对应的相对误差为40% ～56%;局部区域叶绿素a浓度的估算误差较高，如沿湖区域，估算误差小于6 μg/L，其对应的相对误差为32%。

通过上述分析可知，当叶绿素a浓度在20～50 μg/L时，四波段半分析算法的反演精度超过了30%精度的技术极限水平。因此，若采用图4所示的精度描述方式，将导致对叶绿素a浓度反演精度描述的不正确，进而不利于反演数据的应用。另外，与传统方法相比较，基于“带模型”理论的评估方法不仅能获取像元级别的精度描述信息，并适合于表征整个太湖区域的反演精度状况。

3 结论

(1)基于不确定性理论构建的四波段半分析算法的“带模型”表明，反演叶绿素a浓度的估算误差随着反演参数变化呈非规律性变化。当叶绿素a浓度在10～20 μg/L 和50～100 μg/L时，其反演误差较低，大约为±20%;而当叶绿素a浓度在20～50 μg/L时，其反演误差较高，大约为±40%，局部区段高达±60%左右。

(2)由传统方法获取的四波段算法的反演误差指标为21.087%。当叶绿素a浓度在10～20 μg/L和50～100 μg/L时，该误差指标与“带模型”表达的精度信息近似一致，而当叶绿素a浓度为20～50 μg/L时，该指标将失效。由于太湖水体叶绿素a浓度主要分布在20～50 μg/L，因此传统的误差指标不适用于描述太湖水体叶绿素a浓度的反演误差，而“带模型”则能更详细且准确地给出反演结果的误差信息。

参考文献:

［1］Gordon H R，Castaño D J.Aerosol Analysis with the Coastal Zone Color Scanner:A Simple Method for Including Multiple Scattering Effects［J］.Applied Optics，1987，28(7):1320 －1326.

［2］张民伟，唐军武，丁 静.水色大气校正算法综述［J］.海洋技术，2008，27(3):110 －114.

［3］唐军武.海洋光学特性模拟与遥感模型［D］.北京:中国科学院遥感应用研究所，1999.

［4］Shafique N A，Autrey B C，Fulk F，et al.Hyperspectral Narrow Wavebands Selection for Optimizing Water Quality Monitoring on the Great Miami River，Ohio［J］.Journal of Spatial Hydrology，2001，1(1):1 －22.

［5］李小文.定量遥感的发展与创新［J］.河南大学学报:自然科学版，2005，35(4):49 －56.

［6］陈 军，周冠华，温珍河，等.遥感数据误差对地表参数定量反演可靠性的影响——以太湖叶绿素a反演为例［J］.光谱学与光谱分析，2010，30(5):1347 －1351.

［7］Gahegan M，Ehlers M.A Framework for the Modeling of Uncertainty Between Remote Sensing and Geographic Information Systems［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2000，55(3):176－188.

［8］Goodchild M F.Geographical Data Modeling［J］.Computers ＆Geosciences，1992，18(4):401 －408.

［9］史文中，王树良.GIS中属性不确定性的处理方法及其发展［J］，遥感学报，2002，6(5):394 －400.

［10］Perkal J.On Epsilon Length［J］.Bulletin de I＇Academic Polonaise Des Sciences，1956(4):399 －403.

［11］Shi W Z，Ehlers M，Tempfli K.Analytical Modelling of Positional and Thematic Uncertainties in the Integration of Remote Sensing and Geographical Information System［J］.Transactions in GIS，1999，3(2):119 －136.

［12］Renschler C S.Scales and Uncertainties in Using Models and GIS for Volcano Hazard Prediction［J］.Journal of Volcanology and Geothermal Research，2005，139(1/2):73 －87.

［13］Minor E S，McDonald R I，Treml E A，et al.Uncertainty in Spatially Explicit Population Models［J］.Biological Conservation，2008，141(4):956－970.

［14］贺俊华，程永进，张 昊.内陆水体叶绿素a含量定量检测的研究［J］.光学与光电技术，2007，5(5):16 －19.

［15］闻建光，肖 青，杨一鹏，等.基于Hyperion数据的太湖水体叶绿素 a浓度遥感估算［J］.湖泊科学，2006，18(4):327－336.

［16］Goodchild M F.Attribute Accuracy［C］//Proceedings of Elements of Spatial Data Quality，New York，USA:Elsevier，1995:139 －151.

［17］史文中，王树良.GIS数据之属性不确定性的研究［J］.中国图象图形学报，2001，6(9):918 －924.

［18］陈 军，温珍河，孙记红，等.基于四波段半分析算法和Hyperion遥感影像反演太湖叶绿素a浓度［J］.遥感技术与应用，2010，25(6):867－872.

The Uncertainty Model for Water Qualities Retrieval Results:A Case Study of Chlorophyll－a Concentration

CHEN Jun1，2，LU Kai1，2，WANG Bao － jun1，2
(1.The Key Laboratory of Marine Hydrocarbon Resource and Geology，Qingdao 266071，China;2.Qingdao Institute of Marine Geology，Qingdao 266071，China)

With the spectral experiment and the simultaneous observation results of Hyperion satellite on 19 August，2004 as the basic dataset，the authors used the uncertainty principle of spatial data to develop a“bands model”for chlorophyll-a concentration retrieval algorithm of the subsection mapping retrieval model.It is thus found that in the ranges of 10 －20 μg/L and 50 －100 μg/L，the retrieval error of chlorophyll-a concentration is relatively low，(approximately ±20%)，whereas in the range of 20－50 μg/L，the retrieval error of chlorophyll-a concentration is relatively high，(approximately ±40%).A comparison with the traditional methods for error describing shows that the“bands model”could include more detailed and accurate information of data quality for remote sensing products.

Remote sensing;Bands model;Chlorophll-a;Taihu Lake

TP 79;X 832

A

1001－070X(2011)04－0083－04

2011－03－30;

2011－05－03

国土资源部海洋油气资源和环境地质重点实验室基金项目(编号:MRE201109)和中国海陆地质地球物理系列图项目(编号:GZH200900504)共同资助。

陈 军(1982－)，男，主要从事环境遥感和GIS研究。

(责任编辑:李 瑜)