基于COPULA-EVT的利率衍生品风险管理

郑 浩

（武汉大学 经济与管理学院，湖北 武汉 430072）

基于COPULA-EVT的利率衍生品风险管理

郑 浩

（武汉大学 经济与管理学院，湖北 武汉 430072）

监管层提出对“系统重要性银行”和“非系统重要性银行”进行分类管理的思路，表明在强化宏观审慎监管过程中，微观个体宏观审慎经营行为仍然起着重要的作用。新巴塞尔协议对于银行信用风险的监控和计量有了更加严格的规定，然而对于涉及到衍生品的市场风险只是强调银行要根据自身的交易业务进行合理评估，这样便使得衍生品的市场风险成为了银行整体风险中最不稳定的因素。本文基于极值分布、Copula连接函数和蒙特卡洛模拟理论，获得商业银行包括利率期货、利率期权、利率互换在内的单个利率衍生品的风险度量指标，如VaR，CVaR，EVA，RAROC，EC，并得到衍生品组合的风险度量指标，这些指标可以帮助商业银行更加清晰地了解自身的潜在风险。同时，商业银行在给定风险容忍度VaR下能得到各种衍生产品的最优配置，从而为银行的投资决策提供参考。

利率衍生品；风险管理；COPULA;极值分布

一、引言

最近，监管层提出对“系统重要性银行”和“非系统重要性银行”进行分类管理的思路，表明在强化宏观审慎监管过程中，微观个体宏观审慎经营行为仍然起着重要的作用。要完成宏观审慎监管这一过程，仅有监管者的监管原则还不够，还需要银行体系内每个微观个体深入理解监管目标并自觉加以适应。2006年出台的新巴塞尔协议，旨在通过更加完善的资本充足率框架，促进鼓励银行强化风险管理能力，不断提高风险管理水平。新协议对于银行信用风险的监控和计量有了更加严格的规定，然而对于市场风险，特别是涉及衍生品的市场风险并未做出强制性规定，只是强调银行要根据自身的交易业务进行合理评估，这样便使得衍生品的市场风险成为了银行整体风险中最不稳定的因素。

在我国，随着利率市场化进程加快，银行利率敏感性逐渐增强，利率衍生工具需求十分巨大，但我国商业银行的利率风险管理仍处于起步阶段。虽然目前国内各商业银行均持有一定数量利率衍生工具，但规模相对较小且以外币为主。随着中国加入WTO，金融业进入全面开放的新时期：2006年2月央行允许国内商业银行开展人民币利率互换交易试点，利率衍生品开始推出；2006年3月，银行间回购定盘利率正式发布；2007年1月，上海银行间同业拆借利率（SHIBOR）正式上线。虽然现在我国的衍生工具市场尚处于起步阶段，但是衍生市场的发展和衍生工具的广泛应用将会成为未来的发展趋势，随之而来的投机行为所带来的风险也会进一步加大，而对于衍生工具的风险管理，却又是商业银行开展衍生产品业务所必须面对的环节。

鉴于此，本文着力于研究一套能够有效度量利率衍生产品市场风险的方法。VaR方法是市场风险度量过程中常用的方法，处理时可以首先根据衍生产品在窗口期内的每日损益数据，利用相关的方法计算出单个利率衍生产品以及利率衍生产品组合的VaR值，这些VaR值可以反映资产在一定置信水平上的最大损失，使之能在正常市场情况下对资产风险进行较好地描述。尽管VaR方法作为风险管理领域的先进技术已被普遍采用，但是单纯地使用VaR值并不能很好地反映出这些资产在极端情况下所遭受的损失。针对这样的问题，还可以同时引入压力测试。这种方法一般用来测度金融资产对于一些异常但又可信事件的脆弱性，可以作为对VaR方法的完善和补充。

本论文以利率衍生品为研究对象，主要包括利率期货、利率期权、利率互换，针对投机行为，以名义本金为核心概念，通过不同的风险指标和风险度量方法更为准确地度量利率衍生品及其组合的风险，从而帮助商业银行加强利率衍生品的风险管理。具体而言，基于极值分布、Copula连接函数和蒙特卡洛模拟理论，商业银行可以得到单个利率衍生品的风险度量指标，如VaR，CVaR，EVA，RAROC，EC，也可以得到多种利率衍生品组合的风险度量指标，这些指标可以帮助商业银行更加清晰地了解自身的潜在风险。同时，商业银行在给定风险容忍度VaR下能得到各种衍生产品的最优配置，从而为银行的投资决策提供参考。

二、研究思路

（一）分析框架

对衍生产品的风险管理体系可由衍生品资产组合风险度量、压力测试与资本最优配置三部分组成。商业银行利率衍生产品市场风险度量、压力测试和资本最优配置的总体分析框架如图1。

图1 商业银行利率衍生品风险管理总体框架

核心部分风险度量以极值分布、Copula连接函数和蒙特卡洛模拟等技术手段为依托，计算得出非极端情况下利率衍生品资产组合的VaR值、CVaR值以及经济资本；压力测试作为一般情形的补充，可以度量极端情形下银行的损失，根据承压因子的联合分布可以得出专家预测模式和历史情形模式下各种极端事件发生的概率，进而估计资产组合的最大损失，给予银行极端风险评估报告。此外，在实现利率衍生品风险管理功能的基础上，充分考虑到商业银行的盈利性，在风险可控的原则下，通过合理地配置各种利率衍生产品的名义本金，得到收益最大的投资组合。

本文将重点分析基于COPILA-EVT的利率衍生品市场风险度量和资本最优配置。

（二）数据搜集及处理

本文中资产组合选择如下三种利率衍生品资产：（1）5 年期看涨利率期权；（2）2 年期美国国债期货；（3）美元12个月Libor利率互换。其中对于每种资产当日损益的计算分别采取如下的方法：期权的数据选取的是5年利率期权，以最新拍卖的5年债券的到期收益（yield-to-maturity）为基础的每日拍卖价格，期权的收益率=ln本期价格-ln上期价格；期货的数据选取的是两年期美国国债期货每日的价格，期货收益率=ln本期价格-ln上期价格；12个月Libor利率互换，本文选取美元12个月LIBOR作为浮动利率R;再设定一个固定利率r，则利率互换收益率为R-r。①

三、基于COPILA-EVT的利率衍生品市场风险度量

本文采用了基于实时动态数据的市场风险度量方法。首先，运用正态分布和广义Pareto分布拟合各种衍生品收益率的边缘分布；其次，运用copula连接函数进行整合得到资产组合收益率的联合分布函数；最后，利用蒙特卡洛模拟获得资产组合市场风险的VaR值，进而求出精度更高的CVaR（见图2）。

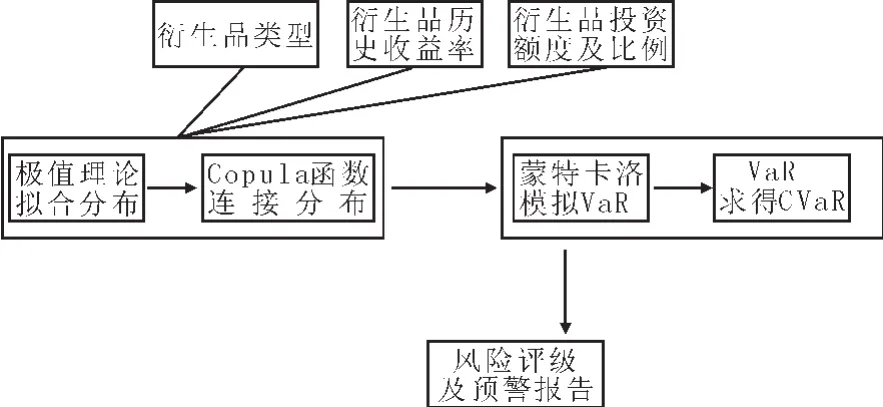
图2 衍生品组合风险度量示意图

（一）用正态分布和广义Pareto分布拟合各种衍生品收益率的边缘分布

金融资产的收益率一般不服从正态分布，而是具有“厚尾”现象。如果采用正态分布的方法进行计算，无疑会低估资产的真实风险，而极值分布方法则较好地解决了这一问题。一般来说，在利用极值理论度量金融风险时主要有两类模型：一类是BMM模型（Block Maxima Model），这类模型主要针对组最大值建模；另一类是广义帕累托模型，简称GPD模型，这一模型对观察中所有超过某一较大门限值（threshold）的数据建模。由于GPD模型有效地使用了有限的极端观察值，因此本文采取这一方法来拟合边缘分布。

在应用GPD模型时，首先是确定某一门限值，找出大于门限值的观察数据；其次，利用极大似然法估计超量损失分布的渐近帕累托分布的参数值；最后，将上述两步中的函数拼接，得到每组数据的边缘分布。边际分布由两种分布三段组合而成，其中GPD为收益率序列的双尾分布，正态分布为收益率序列的中间分布。这种由混合分布构成的边际分布能够依概率收敛于真实的边际收益分布。

处理拟合收益率边缘分布的实现步骤为：

首先，厚尾分布的诊断。对金融资产收益率数据进行基本统计特征的预分析，以判断收益率数据是否具有厚尾性。从QQ图中②可看出，样本数据中间符合正态分布，两端具有厚尾性。

其次，在预分析的基础上，对于不服从正态分布的序列拟合极值理论中运用最广的GPD模型，即对超过某一充分大门限值的数据用GPD建模。

第三，在不同的门限值下分别用GPD函数拟合边缘分布，通过动态的假设检验，选择达到拟合效果最优的门限值。

第四，选定门限值后，用极大似然法估计出正态分布和广义Pareto模型的参数，写出各种衍生品收益率的边缘分布。

1.门限值的选取

（1）通过EMEF图进行初步选取

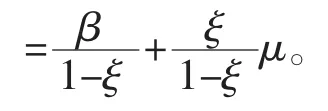
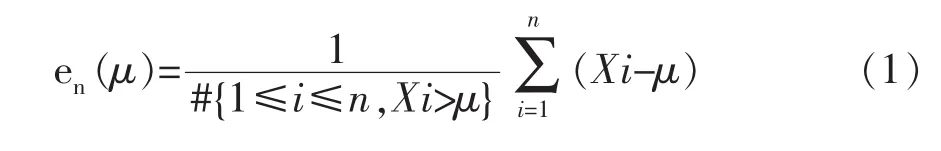
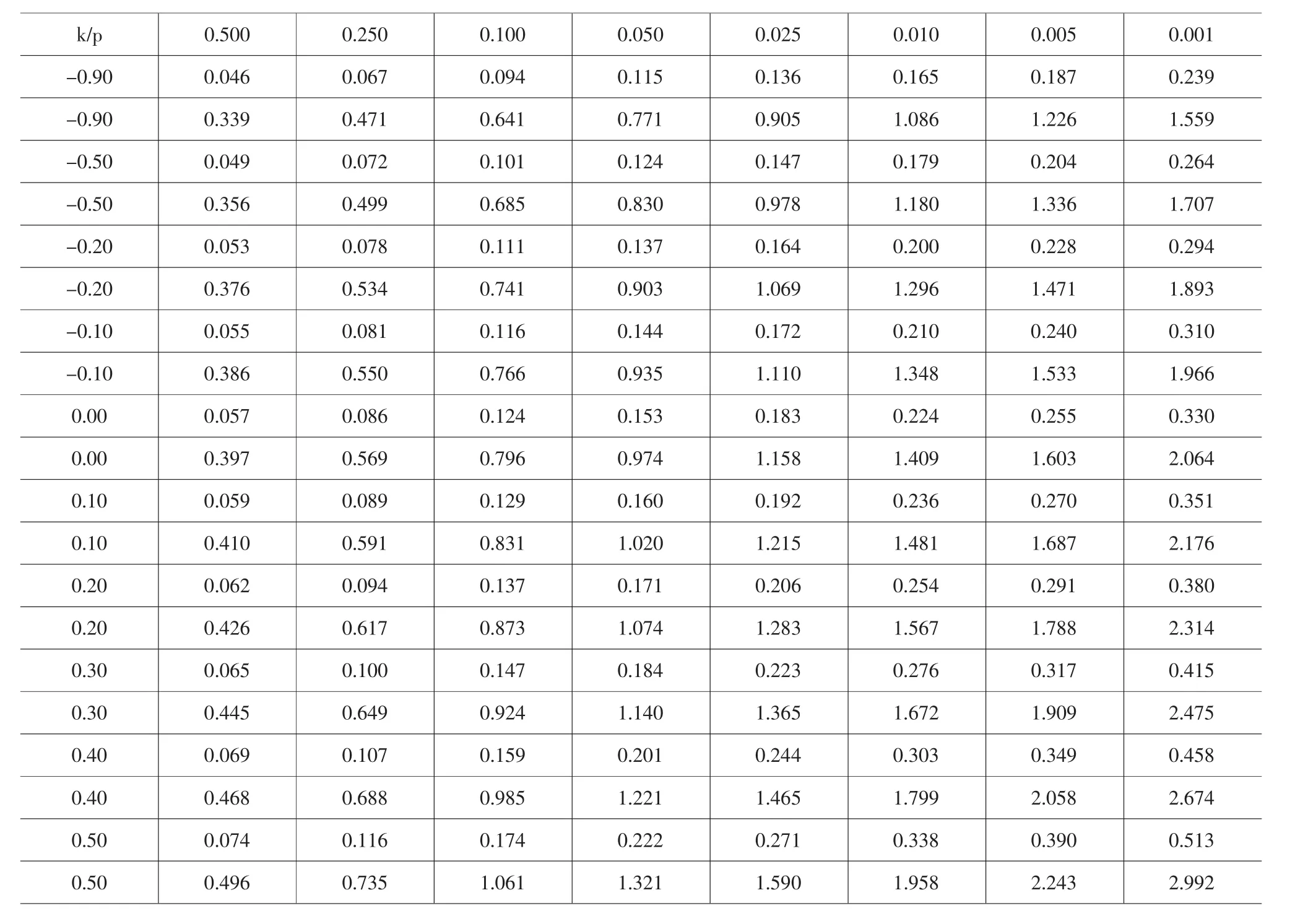
表1 未知 k和 a分别表示 W2和 A2（粗体）尾部的百分点；p为 Pr（W2≥z）或Pr（A2≥z）

在（1）式中，#{1≤i≤n，Xi＞μ}表示在{Xi，i=1，2…n}中比门限值μ大的个数。一般地，如果EMEF在超过某一门限值后有明显的线性变化，且斜率为正时，表明大于此门限值的观测数据服从GPD且形状参数k＞0。根据EMEF图，可看出超出门限值的观测数据应服从GPD且门限值的大致取点在样本数据5%处。

（2）对粗略估计的初始门限值进行假设检验

设μL、μB分别表示资产收益率μR的左右尾部门限值，右尾门限值μR的取法如下：根据（1）中得到的右尾门限值范围的最小值为， 数据采用的部分。重新记同时可用极大似然法估计广义帕累托的参数

对 i=1，2…n，计算 Zi=F（），其中 F（x）=1-（1-kx/a）1/k，为顺序统计量。按照以下公式求统计量W2和A2：

根据表1的情况比较W2和A2各自的P值。这里给定显著水平为0.1，当两者的P值均大于0.1时，所取值即为合理的门限值。否则，除去以上顺序统计量中的最小值， 令为新的预选门限值，记为。用同样方法进行检验，重复此过程，直到得出能够通过检验的门限值μR。

2.三种衍生品的边缘分布函数形式

资产组合中每种金融资产收益率xi的边缘分布为：

）表示小于（大于）门限值

i

（二）运用copula连接函数得到资产组合收益率的联合分布函数

在评估资产组合的市场风险时，目前的方法仅仅将各部分风险价值简单相加，很少考虑资产之间的相关性，这样造成了估算结果与实际情况的巨大差异，严重影响了银行配置资产头寸的合理性。因此，引入一种新的方法，以便能更好地考虑资产组合之间的相关性便成了当务之急，Copula方法恰好能帮助解决这一难题。

Copula函数实际上是一种将联合分布与它们各自的边缘分布连接在一起的函数，能够有效地描述变量之间的相关性，使用Copula函数可以将不同的金融衍生品的收益分布关联起来，得出更为精确的资产组合的风险价值。

运用copula连接函数的主要步骤如下：

首先，选取适当的copula函数。本文采用阿基米德族copula函数中的clayton函数和frank函数，并运用极大似然法分别估计clayton函数和frank函数中的参数。

其次，用信息准则AIC（Akaike Information Criterion）的方法选择最接近真实多元分布的copula函数。

1.构造copula函数

Copula一词原是交换、连接的意思，在数学中它是指把多个变量的联合分布与它们的边缘分布连接在一起的函数。根据Sklar定理：令F为具有边缘分布 F1（·），…，FN（·）的联合分布函数，那么存在一个 Copula 函数 C，满足：F（x1，…，xN）=C（F1（x1），…，FN（xN）），若 F1（·），…，FN（·）连续，则 C 是唯一确定的。

对于多元连续分布函数，一元边缘分布函数和多元分布函数相关结构能够被分离，多元变量之间的相关结构可以用适当的Copula函数表示。Copula函数的类型很多，总体可以分为椭圆类分布连接函数和阿基米德连接函数，而每类又分为许多具体的连接函数。本文采用阿基米德族copula函数中的clayton函数和frank函数：

其中 u1、u2、u3分别表示收益率边缘分布 F1、F2、F3。

有了确定的收益边缘分布Fi，可以对copula函数采用半参数估计，即边缘分布为已知，但copula参数未知，采用极大似然法估计copula参数α。

2.Copula函数的最优选择

由于难以判定某一种Copula绝对优于另一种，本文希望样本数据能够对Copula函数做出自适应选择，即选择最接近真实多元分布的Copula函数。这个过程可以用信息准则AIC（Akaike Information Criterion）的方法来实现。

由上一步极大似然估计法得到的Copula参数αˆ建立AIC统计量：

对于多个Copula的最优选择也可以重复这个两两检验的过程。

（三）运用蒙特卡洛模拟获得资产组合市场风险的VaR、CVaR值

在金融衍生产品（期权、期货、掉期等）交易风险估算中，问题的维数可能数以千计。对这类问题，难度随维数的增加呈指数增长，这就是“维数的灾难”（Course Dimensionality），传统的数值方法难以应对。

蒙特卡罗（Monte Carlo）方法是一种基于“随机数”的计算机随机模拟方法，它能很好地用来应对维数的灾难，因为该方法的计算复杂性不再依赖于维数。因此，本文应用Monte Carlo模拟计算投资组合的VaR，进而求出精度更高的CVaR。

1.Montecarlo模拟得出每种资产收益率序列

处理步骤如下：

首先，产生一个随机数序列（v1，v2，v3），且均服从独立的［0，1］均匀分布。

第三，通过边缘分布，由（u1，u2，u3）得到收益率序列（x1，x2，x3），其中（x1，x2，x3）=（F-1（u1），F-1（u2），F-1（u3））。

2.获得资产组合市场风险的VaR，CvaR

给定投资组合权重（w1，w2，w3），得到组合收益R=w1x1+w2x2+w3x3，重复以上montecarlo模拟步骤N次能够得到N组收益率R1，…，RN，按照从小到大在坐标轴上排列，取左端1%处值为VaR值。

图2 基于不同风险度量方法的资产组合选择边界

CVaR是指损失超过VaR条件下的平均损失，设损失X的分布函数为F（x），则其置信度为α的CVaR 定义为 CVaR=E［X|X＞VaRα］。 通过改变投资组合的权重，重复上述步骤，可以得到不同投资组合的CVaR值。

四、经济资本约束下的最优资本配置

最优配置能使得经济体能最大限度地获得更多的利润，也能帮助经济体最大可能地降低风险，银行系统同样有必要考虑最优化问题，其目标是将资本和银行资产的非预期损失保持一个合理的水平，最大化银行的收益。这与商业银行稳健经营，在风险可控的范围内实现收益最大化的目标是完全一致的。

最优配置的基本原则是在资产组合基础上，充分了解风险分布状况，并据此分配持有头寸。科学分配投资数额需要三个前提：第一，了解各种风险的概率分布;第二，了解并估计各种风险敞口的额度，以及这些敞口的相关性;第三，设定银行对风险的容忍程度。

在给定的VaR值的情况下，计算投资组合使得期望收益最大，得到的资产组合即是银行在给定风险容忍度 VaR 下的最优配置，记为（w1，w2，w3），它是以下问题的解：

S.T.VaR=（w1，w2，w3）≤1*q

其中q为银行的风险容忍度。

处理步骤如下：

首先，根据（4）式，每次使用最近3个季度的数据可以拟合三种产品的分布函数。三种产品资产组合的联合概率密度函数为 c{f1，f2，f3，α}*f1*f2*，其中

其次，假设银行给定置信水平a%下的VaR值，最优配置w1、w2、w3满足下列最优化问题：

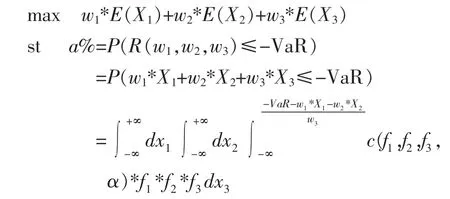
其中 E（Xi）（i=1，2，3）为这三种资产的平均收益率，可以根据前面步骤中拟合出的边缘分布函数进行期望值求解得出。

五、结语

在强化宏观审慎监管过程中，微观个体宏观审慎经营行为仍将起着重要的作用。新巴塞尔协议中对于涉及到衍生品的市场风险未能做出明确的规定，这样便使得衍生品的市场风险成为了银行整体风险中最不稳定的因素。本文基于极值分布、Copula连接函数和蒙特卡洛模拟理论，得到了商业银行包括利率期货、利率期权、利率互换在内的单个利率衍生品的风险度量指标，也可以得到多种利率衍生品组合的风险度量指标，这些指标可以帮助商业银行更加清晰地了解自身的潜在风险。

大部分金融衍生品的收益率分布及其波动行为具有与正态假设不相符的特征，主要体现在资产收益率分布存在尖峰厚尾现象。本文针对传统资产组合选择模型采用方差或标准差度量风险的不足，充分利用了收益率分布的尾部极端数据，构建了基于Copula-EVT函数的资产组合选择模型，对银行利率衍生产品及组合进行了风险度量。以往的风险管理在估算资产组合的风险时往往忽略了资产间的相关性，或只考虑二维情况下的协方差问题，使得银行不能准确地配置资本头寸。本文通过Copula函数较为精确地刻画三种资产间的相关性问题，基于此在给定商业银行风险容忍度的情况下还能得出合理的最优资本配置。

本文有待扩展的地方是：为应对极端情形，一套完善的风险管理体系还应当包括压力测试部分。对于市场风险，特别是针对利率衍生品市场风险这一领域并没有相关成熟的理论，可以通过挑选股票市场指数、原油价格指数以及利率指数等作为影响利率衍生品收益率及VaR值的承压因子，并得出它们的联合分布；然后根据三个因子的联合分布分别得出专家预测模式下和历史情形模式下的出现概率；最后，可以根据极值理论下的计算给定概率VaR的公式得出不同极端情况下的VaR值。

注 释：

① 期权数据来源于芝加哥交易所，期货数据来源于路透网，互换数据来源于凤凰网。

② QQ图的解释是：如果数据独立同分布，均服从正态分布，正态QQ图中的点应该近似是一条直线；否则表明经验分位数比理论分位数增长快，这时分布是厚尾的。

③ 每种产品分别有三段函数，因此此处考虑的产品组合中应有27段函数。

[1]温家宝.政府工作报告[R].北京：人民出版社，2011.

[2]巴曙松，王凤娇，孔颜.系统性金融风险的测度方法比较[J].湖北经济学院学报，2011，（1）：32-39.

[3]韦艳华，张世英.金融市场的相关性分析——Copula-GARCH 模型及其应用[J].系统工程，2004，（04）：7-12.

[4]吴振翔，叶五一，缪柏其.基于Copula的外汇投资组合风险分析[J].中国管理科学，2004，（4）：2-6.

[5]张尧庭.连接函数（copula）技术与金融风险分析[J].统计研究，2002，（4）：48-51.

[6]A.C.Davison，R.L.Smith.Models for Exceedances over High Thresholds[J].Journal of the Royal Statistical Society.， 1990， 52（3） ：393-442.

[7]Enrique， C&Ali， S.H.Fitting the Generalized Pareto Distribution to Data[J].Journal of the American Statistical Association， 1997， 92（440）：1609-1620.

[8]Palaro H P，Hotta L K.Using Conditional Copula to Estimate Value at Risk[J].Journal of Data Science，2006， 4（1）：93-115.

[9]V.Choulakian，M.A.Stephens.Goodness-of-Fit Tests for the Generalized Pareto Distributions[J].Technometrics， 2001， 43（4）：478-484.

Risk Management for Interest Rate Derivatives by COPULA-EVT

ZHENG Hao
(Economic and Management School，Wuhan University，Wuhan Hubei 430072，China)

Regulators proposed the idea for commercial bank's category management by“systemically important bank ”and“non-systemically important bank”,which indicates that the behavior of micro-individual still plays an important role in macro prudential management.Basel II gives more stringent monitoring and measurement requirements for banks'credit risk management,but ignored market risk related to derivatives,and this will bring about the most destabilizing factor to bank's overall risk management.In this paper we are aiming to strengthen interest rate derivatives related risk management for the commercial banks by means of different risk indexes and risk metrics methods.Based on the techniques of extreme value distribution，copula function and Monte Carlo Simulation，commercial banks will have access to risk metrics indexes such as VaR，CVaR,EVA,RAROC and EC，also the portfolio.Besides，optimal economic capital allocation is also can be considered to rationally allocate the notional principal with the limitation of economic capital in order achieve the portfolio with maximum yield.This will be a good combination of the profitability and safety of a commercial bank.

interest rate derivatives;risk management;COPULA;extreme value distribution

F069.9

A

1672-626X（2011）03-0031-07

2011-03-01

郑浩（1985-），男，湖北汉川人，武汉大学经济与管理学院博士研究生，主要从事数理经济学研究。

刘同清）