二维无序系统无序度和本征能量对局域化长度的影响

冯立峰，姚成宝，张 强

（哈尔滨师范大学物理与电子工程学院，

低维体系与介观物理省重点实验室，黑龙江 哈尔滨 150025）

二维无序系统无序度和本征能量对局域化长度的影响

冯立峰，姚成宝，张 强

（哈尔滨师范大学物理与电子工程学院，

低维体系与介观物理省重点实验室，黑龙江 哈尔滨 150025）

利用蒙特卡洛模拟方法，研究了无序度和本征能量对局域化长度的影响.研究结果表明：随着无序度的增大，系统的电子态出现局域化现象，局域化长度逐渐减小，而且对应于不同的能量本征值；电子的局域化程度不同，能带中心出现准扩展态，系统内部出现类金属行为.

无序系统；Anderson模型；局域化；蒙特卡洛模拟

晶体结构中电子的波函数是布洛赫函数.当晶体系统的有序结构被破坏时，系统的电子态会发生很大的变化.Anderson指出由于系统无序导致电子局域化［1－5］.在对无序系统电子态的研究中，Anderson只考虑了短程跳跃中的最近邻跳跃，构造了著名的Anderson模型.Anderson模型是一个简单的紧束缚模型，无序性是指在每一个格点的能量不同.无序性是随机的，在一固定的组态下，哈密顿量可写为

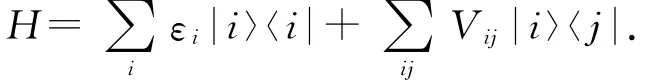
式中：εi为电子格点i的能量，满足某种概率分布p（εi）；Vij为电子从j点跃到i点的跳跃能.理想的哈密顿量与实验体系的哈密顿量就有很大的差别，同时又由于无序性的引入使简单的哈密顿量也很难得到严格的解.

可见无序系统处理起来相当复杂，很多学者在研究无序时总是采用单电子近似下的一维无序Anderson模型［2－3］.不过一维模型毕竟是一个过于简化的模型，其局限性非常明显.本文从单电子近似下无序Anderson模型出发，借助蒙特卡洛模拟研究方法，模拟了二维无序系统中局域长度随系统的本征能量和无序度的变化关系.

1 无序度W对局域化长度L的影响

无序度W对局域化长度L的影响非常明显.在系统中，局域化长度反映电子的局域化程度，同时也是考察系统导电性能的重要指标，所以无序度W影响着系统的金属或绝缘行为［6－14］.

对于二维无序系统，可以看成带状结构.从运算精度考虑，当带长N取200 000时就已经构成了一个非常理想的无序系统，这时已能显示无序系统电子结构的稳定性.

我们选取本征能量E＝0，带宽M＝10，带长N＝200 000，得到局域化长度L随无序度W的变化规律曲线，如图1a.

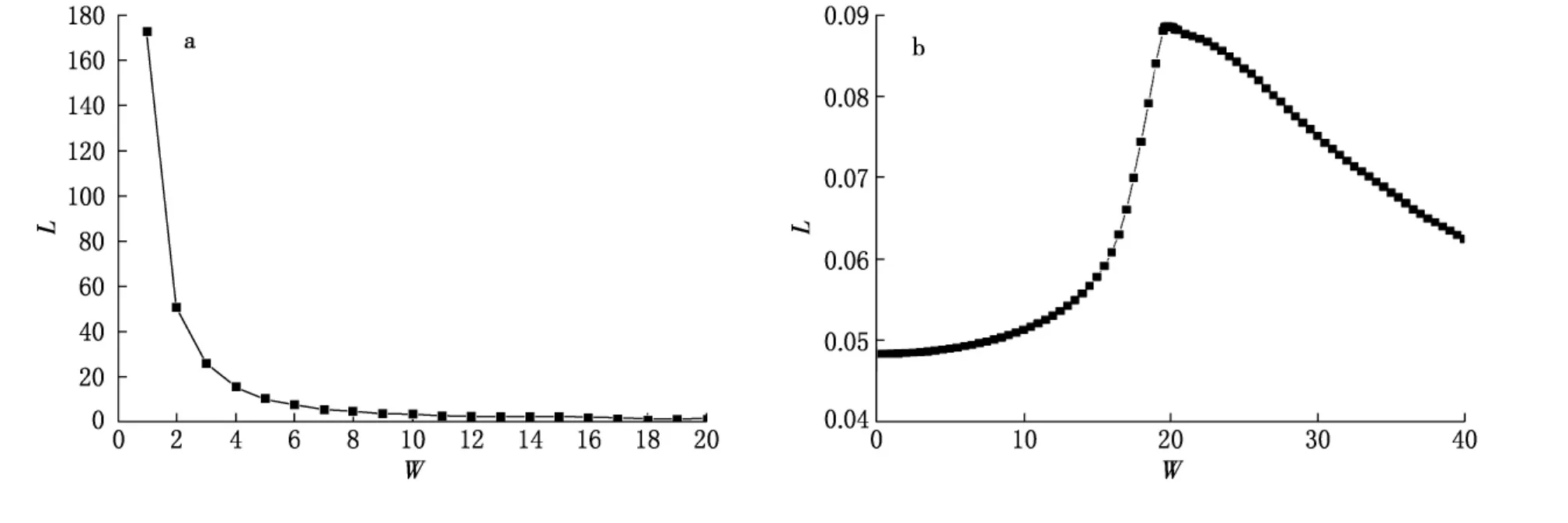
图1 L随W的变化规律曲线

当W＜5时，L值迅速减小；当W＞5时，L值减小得非常缓慢.总体来说，随着W的增大，L值逐渐减小，即随着无序度的增大系统的电子态出现局域化现象.这符合电子输运理论，随着系统无序度的增加，晶格中电子的扩散运动受阻，因此系统的局域化程度被加强.

当选取E＝10，M＝10，N＝200 000时，得到的模拟结果见图1b.对比图1a和b可以看出，改变本征能量E值，发现模拟得到的曲线中，局域化长度存在极值，极值点处于W＝20.

分析图1b中出现这种现象的原因，可能的解释是本征能量E和无序度W的双重影响，使得系统内的格点势发生了改变，无序系统中电子的输运性质以及局域化程度发生了改变，电子的局域输运性质出现了不同寻常的行为［2］.

2 本征能量E对局域化长度L的影响

从图1看出，M和N值不变而改变E值，得到的L随W变化的模拟结果不同，可见本征能量E对局域长度L一定存在某种影响.

选取W＝5，N＝200 000，M＝20和M＝10，E值的区间为［－15，15］见图2a.从图2a中看出，能量本征值不同，局域化程度亦不同.能带中心区域局域化长度比远离能带中心处的局域长度大几十直至上百倍，甚至超过了带宽，即能带中心部分出现了准扩展态，系统内部出现类金属行为.还可以看出，能带中心E＝0附近出现了双峰现象.不知这种现象是否与二维系统有关系，目前还不清楚，我们正在寻求合理的理论解释.

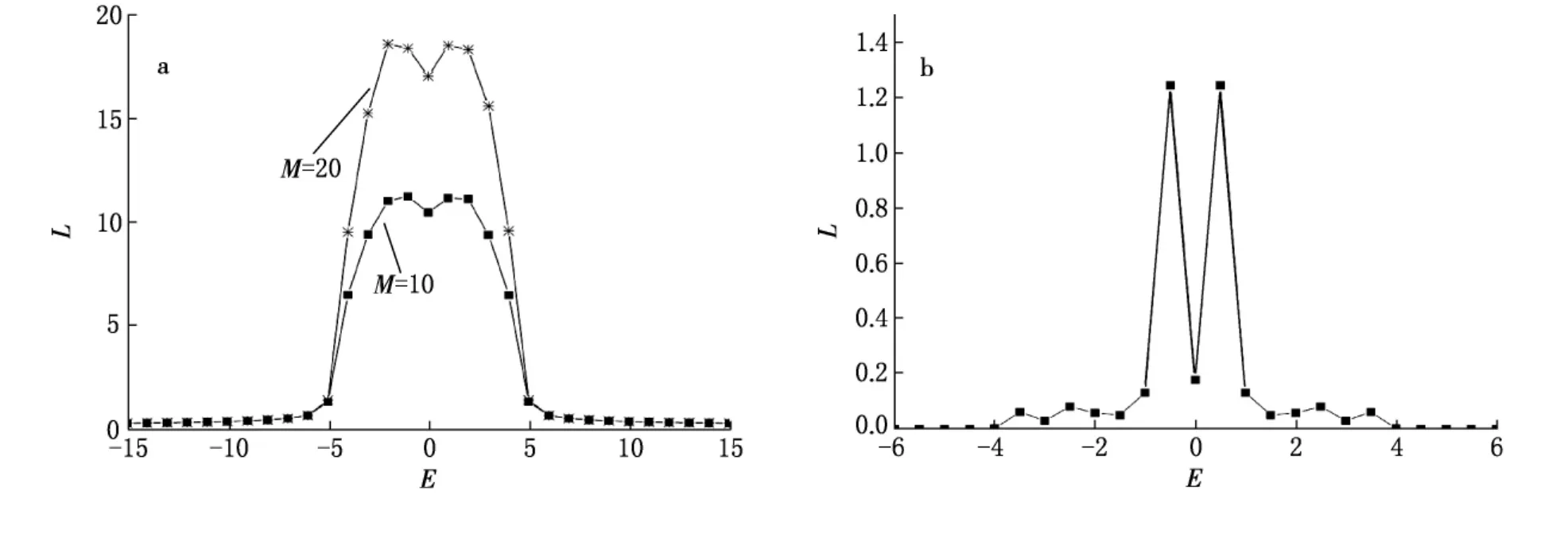
图2 L随E的变化规律曲线

为了进一步观察双峰现象，我们选取一个有序系统，令W＝0，M＝10，N＝200 000，得到图2b.

从图2b仍可观察到能带中心附近出现了双峰现象，并且峰值所代表的L值完全可以和系统尺寸比拟，甚至远远大于系统尺寸，此即表示有序系统中存在扩展态，系统表现为金属行为.

3 结论

无序系统的电子理论较之有序系统要复杂得多，研究起来往往需要使用更多的数学工具.本文采用蒙特卡洛方法模拟了二维无序系统局域长度与系统无序度和本征能量的关系.研究结果显示：随着增大系统的无序度，系统的电子态出现局域化现象.能量本征值不同，电子被局域化的程度将有很大的不同，能带的中心区域，局域化程度较弱，然而当能量本征值越大时，局域化程度越高.在能带中心部分的局域化长度比远离能带中心处的局域化长度大几十甚至上百倍，即能带中心出现了准扩展态，系统内部出现类金属行为.

［1］ ANDERSON P W.Absence of diffusion in certain random lattices［J］.Phys Rev，1958，109（5）：1492-1505.

［2］ 刘小良，徐慧，马松山，等.一维无序二元固体中电子局域性质的研究［J］.物理学报，2006，55（6）：2949-2954.

［3］ 徐慧，宋祎璞，李新梅.一维无序体系电子跳跃导电研究［J］.物理学报，2002，51（1）：143-147.

［4］ 田强，涂清云.凝聚态物理学进展［M］.北京：科学出版社，2005：38-51.

［5］ 马文淦.计算物理学［M］.北京：科学出版社，2005：95-100.

［6］ ANDERSON P W，THOULESS D J，ABRAHAM E，et al.New method for a scaling theory of localization［J］.Phys Rev B，1980，22（8）：3519-3526.

［7］ ABRAHANS E，ANDERSON P W，LICCIARDELLO D C，et al.Scaling theory of localization：absence of quantum diffusion in two dimensions［J］.Phys Rev Lett，1979，42（10）：673-676.

［8］ XIONG S J，ZHANG G P.Scaling behavior of the metal-insulator transition in one-dimensional disordered systems with longrange hopping［J］.Phys Rev B，2003，68（17）：174201-174203.

［9］ SHIMA H，NOMURA T，NAKAYAMA T.Localization-delocalization transition in one-dimensional electron systems with long range correlated disorder［J］.Phys Rev B，2004，70（7）：075116-075121..

［10］ FRANCISCO A B F，DE MOURA，MARCELO L LYRA.Delocalization in the 1DAnderson model with long-rang correlated disorder［J］.Phys Rev Lett，1998，81（17）：3735-3738.

［11］ RODRIGUEZ A，MALYSHEV V A，SIERRA G，et al.Anderson transition in low-dimensional disordered systems driven by long-range nonrandom hopping［J］.Phys Rev Lett，2003，90（2）：027404-027407.

［12］ SAMUKHIN A N，PRIGODIN V N，JASTRABÍK L et al.Hopping conductivity of a nearly 1Dfractal：a model for conducting ploymers［J］.Phys Rev B，1998，58（17）：11354-11370.

［13］ MASCHKE K，SCHREIBER M.Electron transport along a spatially disordered chain in the presence of dissipation［J］.Phys Rev B，1994，49（4）：2295-2305.

［14］ FOGLER M M，TEBER S，SHKLOVSKII B I.Variable-range hopping in quasi-one-dimensional electron crystals［J］.Phys Rev B，2004，69（3）：035413-035430.

Influence of the disorder and the eigenenergy on localization length in the two-dimensional disordered system

FENG Li-feng，YAO Cheng-bao，ZHANG Qiang
（School of Physics and Electronic Engineering，Harbin Normal University，Heilongjiang Key Laboratory for Low Dimensional System and Mesoscopic Physics，Harbin 150025，China）

By using Monte Carlo simulation method，the influence of the localization length is studied as a function of the disorder and eigenenergy in disordered system.The results derive that electronic states of system exhibited localization phenomena with the increase of degree of disorder and the localization length can be reduced gradually.Moreover the degree of electronic localization is different for different energy eigenvalue，the quasi extended state appears at the center part of energy band and quasi-metal behavior emerges in the disordered system.

disordered system；Anderson model；localization；Monte Carlo simulation

O 469

140·50

A

1000-1832（2011）03-0073-03

2011-01-27

黑龙江省自然科学基金资助项目（A200807）；黑龙江省教育厅科研项目（11541108）.

冯立峰（1973—），男，硕士，讲师，主要从事低维体系电输运性质的理论研究.

石绍庆）