月表无线电波传播建模与仿真

黄丽霞

(北京空间飞行器总体设计部,北京 100094)

1 引言

月球探测工程是近年来航天领域的研究热点。我国已经成功实现了绕月工程,下一步将实现月球软着陆探测和巡视勘察。要设计着陆器与月面巡视器之间的月面通信信道,需对月面两器之间的通信链路进行仿真分析。与以往的卫星对地信道不同,月面通信采用V HF/UHF频段,波长在0.1～10m范围内。月表障碍物及月球曲率的影响,会产生球形月面绕射(由月球形状引起)、多径干涉效应(由月表对电波的反射引起)和多峰绕射(由月面的环形山等障碍物引起)等现象,所有这些都将影响月面两器之间通信信道的设计。

针对地球表面各种环境下的电波传播特性,国内外均有较多的研究(如文献[1-4]等),国际电联(ITU)也针对传播路径上各种障碍物的特点建立了一系列绕射模型[5]。但是,针对某一特定环境的多径干涉和绕射效应的完整传播模型,还需要通过具体分析才能建立。本文针对月球曲率比地球曲率大很多的特点,在假设月表光滑的前提下,对月表无线电波传播进行建模、仿真研究,为月表通信信道的设计提供了仿真分析手段和理论支持。

2 月表无线电波传播模型建模

与地面电波传播类似,月面附近的电波传播主要考虑月面反射多径干涉和绕射效应。从算法实现的角度来看,多径干涉和绕射效应属于此消彼长的关系。在一次传播过程中,目标或处于多径干涉区,或处于绕射区,或处于干涉区和绕射区之间的过渡区。建立月表无线电波传播模型的关键问题,在于对目标究竟处于干涉区、地形障碍物绕射区,还是球形月面绕射区进行准确判断。

与地面环境不同,月球大气非常稀薄,通常认为月球没有大气,接近真空环境。因此,在建立月表电波传播模型时,主要考虑多径干涉和绕射效应,不考虑大气传播衰减和大气折射。由于传播路径上单个障碍物的绕射传播模型本身已很成熟,且与地形数据紧密相关,为了在系统层面上对电波传播损耗变化规律进行仿真分析,本文在建立月表传播模型时假设月表平缓,而没有对路径上单个障碍物的影响进行分析,即只考虑月球曲率的影响。本文以类似宽广平原的月海地貌为通信环境,因此在工程估算上,作表面平缓的假设是合理的。

2.1 多径干涉和绕射效应原理模型

一般,按电波传播距离可分为视距传播和超视距传播。视距传播是指在发射天线和接收天线间能相互“看见”的距离内,电波直接从发射点传播到接收点(一般包括地面的反射波)的一种传播方式。当发射天线和接收天线之间的距离大于最大视距时,电波通过绕射到达接收天线,即为超视距传播。

在视距范围内,一般考虑表面反射多径的传播模型。由于月球曲率较大,在视距范围内月表凸起,也会对第一费涅尔区造成一定程度的遮挡,因此视距范围内仍需部分考虑绕射影响。文献[5]中对传播路径上的障碍物建立了单刃峰、双刃峰和单圆顶峰等多种传播模型,假设月表平缓,无其他地形障碍物,发射天线和接收天线之间的障碍物为月球曲率引起的凸起月表。将月表看成一个巨大的圆表障碍物,视距内绕射模型可考虑采用圆表障碍物绕射模型,也可考虑采用球形地面绕射模型。在超视距情况下,电波的传播以绕射为主,一般采用球形地面绕射模型进行绕射损耗的计算。

2.1.1 反射多径干涉传播模型

多径干涉效应是指雷达发射的电波到达目标的路径不止一条,包括一条直射路径和一条或多条反射路径,直射波与反射波在接收天线处形成干涉场[6]。在有光学视距的情况下,由于发射天线和接收天线都接近月表面,电波传播一般可以仅考虑从发射天线到接收天线的直射波及月面反射波的双射线传播模式,接收点处的场强为直射波和反射波在该点的干涉叠加。图1为双射线传播模式示意图。其中:O为反射点;h1和h2分别是发射天线和接收天线的高度;d1和d2分别为反射点到发射天线和接收天线的月面距离;发射天线和接收天线之间的月面距离d =d1+d2;θ为反射波的仰角,θd为直射波的仰角,θA为发射天线波束的仰角,Rd为发射天线和接收天线之间的斜距。通过几何关系可以得到,半径为R 的球面上高度分别为h1和h2的两天线间的视距为

“轴”一般指的是把具有增长潜力的主导产业集聚区或产业集聚城镇联系起来的基础设施带，如公路、铁路、河流等。科学合理地选择发展轴是体育小镇空间布局的关键。在分析江苏省社会经济发展格局，交通环境及水文地理条件等基础上，笔者选取江苏大运河体育文化带、环太湖体育圈、长江体育产业带作为江苏省体育小镇空间布局的发展“轴”。

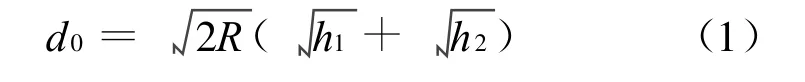
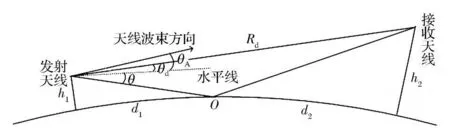
图1 双射线传播模式Fig.1 Double-radial propagation mode

当发射天线与接收天线之间的月面距离d 已知时,可按文献[6]中给出的以下公式来求解反射点的位置,计算出反射点到发射天线的月面距离d1。

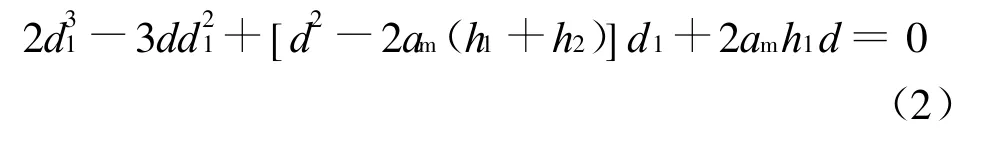
式中:am为月球半径。

根据几何关系,传播余隙Hc(传播路径上的障碍物最高点到发射点和接收点连线的垂直距离)可以由下式计算

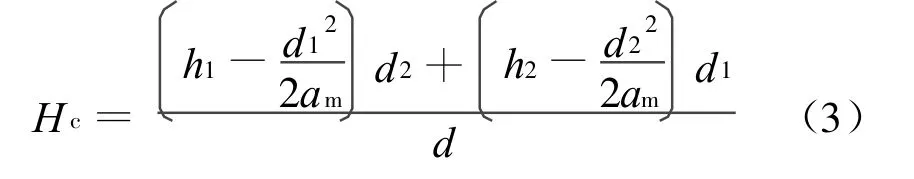
在视距内双射线多径传播模型下,接收点位置的合成场强E可表示为[6]

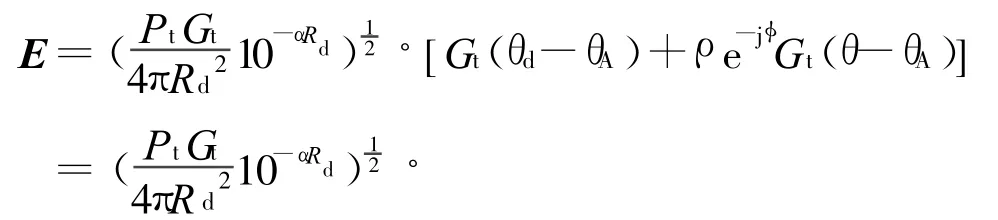
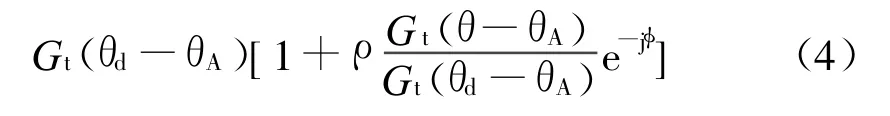
式中:Pt为天线发射功率;Gt为发射天线增益,Gt(θ-θA)为发射天线方向图;φ为反射面的电波反射特性与反射波和直射波之间的程差引入所产生的相位延迟;α为大气衰减因子;ρ为反射面的反射系数,ρ=ρ0·D·γ,其中,ρ0为平滑表面的反射系数,它不仅取决于材料的电磁特性,还与入射余角及波的极化方式有关,D为反射面为球面而引起的扩散因子,γ为粗糙度因子,具体计算公式可参考文献[6]。

月面反射衰减可表示为

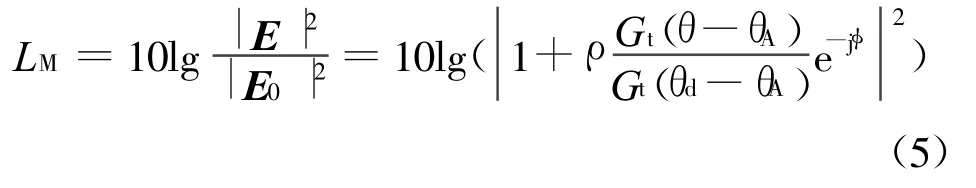
式中:LM为反射多径损耗;E0为自由空间场强。

2.1.2 球形月面绕射模型

绕射效应通常是指以下两种情形[6]:一是电波传播到电波直视距离之外的某个区域;二是发射天线和接收天线之间有高山或高大建筑物,电波绕过障碍物传播到阴影区的现象,也称为衍射。根据月球形状以及月表障碍物形状的不同,绕射可分为球形月面绕射、单刃峰绕射、单圆顶形障碍物绕射、非刃峰绕射和多峰绕射。其中:球形月面绕射由月球曲率引起,用来表示波束照射到月平面以下的现象;其余则是由传播路径上的山峰等引起。

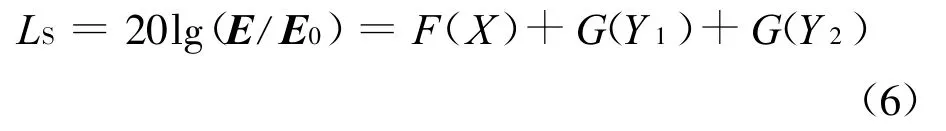
忽略月表其他障碍物的影响,超视距情况下的球面绕射传播可以采用文献[5]和[7]的公式进行仿真。超视距范围的电波绕射传播场强E ,相对于自由空间场强E0的关系式如下式中:LS为球形月面障碍物绕射损耗;变量X是标准化的发射天线和接收天线之间的路径长度,X =2.2βf1/3am-2/3d,其中,f为电波载波频率,单位是M Hz,β是与月表特性和极化方式相关的参数,对于多数情况,即水平极化或频率大于20M Hz 的垂直极化,β为1;Y1和Y2是标准化的发射天线和接收天线高度,距离增益项F(X)=11 +10lg(X)-17.6X ,单位为dB;G(Y1)、G(Y2)分别为发射天线和接收天线的高度增益项,单位为dB,G(Y)的表达式见式(7)。这里,d 和am的单位是km ,h1和h2的单位是m。

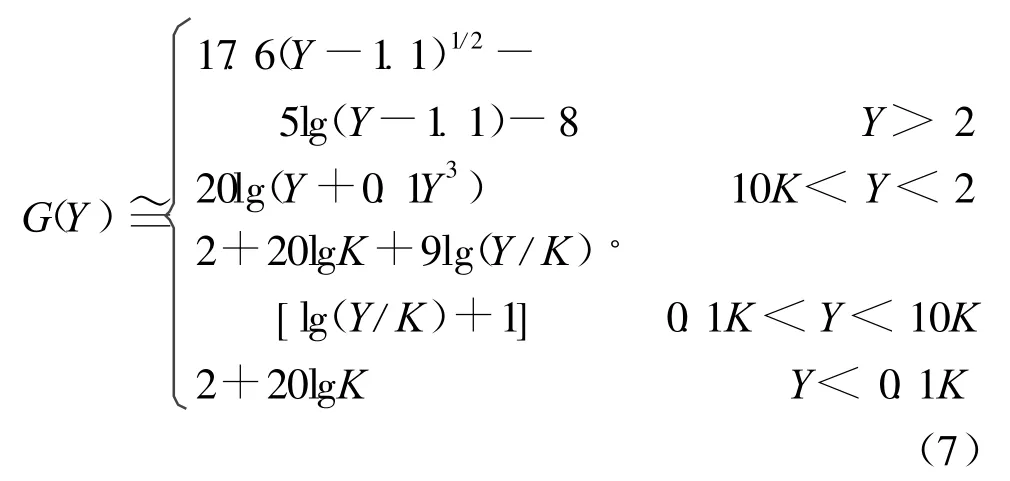
式中:K是一个标准化的因数,用来表征月表的电特性对电波衍射传播的损耗影响,水平极化因数KH和垂直极化因数KV可表示为

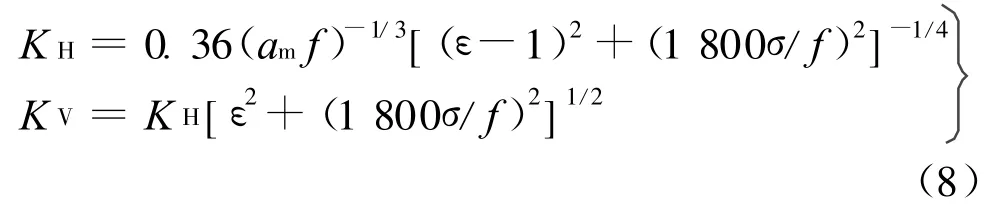
式中:ε为月壤相对介电常数;σ为月壤电导率。

2.1.3 圆表障碍物绕射模型

障碍物表面的包络近似为圆弧形的障碍物,称为圆表障碍物。微波工程上常用的圆表障碍物绕射损耗LD的计算式为

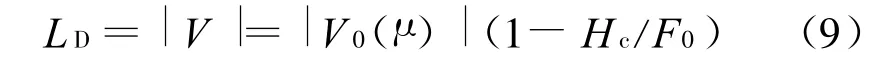
2.2 光滑月表无线电波传播模型

2.2.1 基于标准多径干涉和绕射算法的月表传播模型

建立光滑月表无线电波传播模型,需要对2.1节中各基本原理模型的应用条件进行判断分析。根据惠更斯-费涅尔原理,从发射点到达接收点的电磁能量是通过费涅尔区来传播的。其中,第一费涅尔区是传播能量最集中的区域[8-9]。随着费涅尔区号的增大,在接收点处产生的场强近似以等差级数递减,而相邻费涅尔区的相位相差180°。

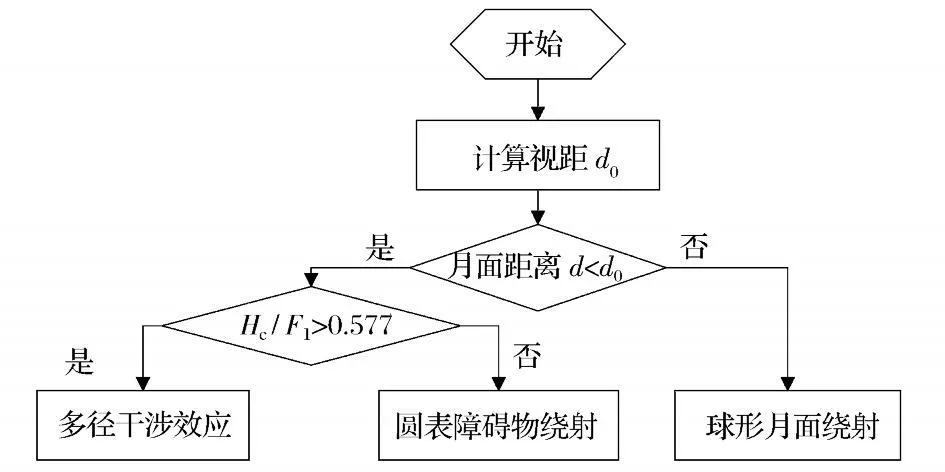
图2 基于标准多径干涉和绕射算法建立的月表无线电波传播模型Fig.2 Lunar-surface radio wave propagation model based on standard multipath and diffraction algorithm

至此,基于标准多径干涉和绕射算法的月表无线电波传播模型已初步建立。关于该传播模型对月表电波传播特性描述的精确性,暂时无法在地面上进行验证。另外,虽然月球曲率远大于地球曲率,将视距内月表凸起作为一个巨大的圆表障碍物来处理是否合理,还有待验证。

2.2.2 基于SEKE算法的月表传播模型

美国林肯实验室关于多径干涉、球形地面绕射和多刃峰绕射的研究算法,即球形地球刃峰衍射(SEKE)算法[1],是在标准多径干涉和绕射算法的基础上更为精细的完整算法,对复杂地形环境下的电波传播建模具有广泛的参考意义。本文参考S EKE算法,针对月表光滑的假设,建立月表电波传播模型,如图3所示。

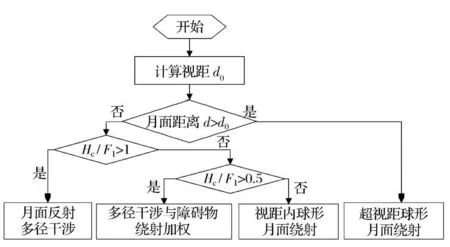
图3 根据SEKE算法建立的月表无线电波传播模型Fig.3 Lunar-surface radio wave propagation model based on S EKE algorithm

根据图3,本文主要考虑月面反射多径干涉、多径干涉与障碍物绕射加权和球形月面绕射3 种情况。在视距范围内,Hc/F1＞1时,表示传播余隙Hc比较大,忽略绕射影响,仅考虑反射多径模型,L =LM;0.5 ＜Hc/F1＜1时,表示直射波的第一费涅尔区轻微被遮挡,多径干涉和障碍物绕射影响均需考虑,L =aMDLM+(1-aMD)LS,加权因子aMD=2Hc/F1-1 ;0 ＜Hc/F1＜0.5时,直射波的第一费涅尔区被遮挡情况较重,此时可理解为月面反射波的第一费涅尔区被遮挡情况更严重,因此可以忽略反射多径的影响,除考虑自由空间传播路径损耗外,主要考虑球形月面障碍物绕射损耗,L =LS。当发射天线和接收天线之间的距离d ＞d0,电波进入超视距传播模式时,传播余隙Hc＜0 ,电波传播以绕射为主,采用球形月面绕射模型,L =LS。

设月表电波传播总损耗为Ltotal,自由空间传播路径损耗为,单位均为dB,则

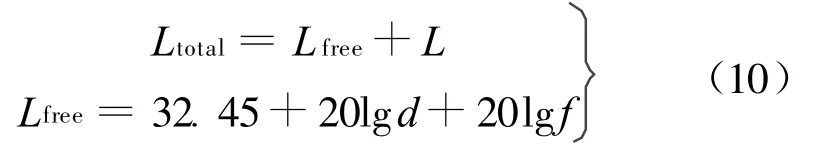
3 仿真结果分析

设发射天线和接收天线高度分别为1m 和3m,测控频率为300MHz。已知月球半径为1 738km,根据式(1)可知,两天线视距约为5km。假设月壤相对介电常数为3,电导率为10-3S/m。考虑到月球探测器的着陆点及移动区域主要在月海,相当于平原,故用于计算粗糙度因子的月面高度标准偏差取1m。极化方式设为水平极化。仿真案例暂不考虑天线方向图对功率的影响。仿真结果见图4。图中分别给出了基于标准多径干涉和绕射算法以及基于SEKE算法建立的传播模型所计算的传播损耗随距离变化的曲线,并给出了相应距离下自由空间损耗变化曲线作为结果分析的参考。

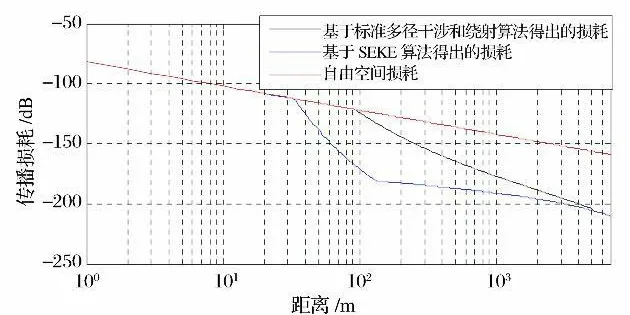
图4 传播模型计算结果Fig.4 Calculation results of propagation models

从图4可以看出,基于标准算法建立的月表传播模型,路径损耗有两处拐点。第一处为Hc/F1=0.577 的位置(本算例中约100m 处),之前近似为自由空间传播损耗,之后由于最小费涅尔区受阻,增加了绕射损耗(采用圆表障碍物绕射模型计算),曲线斜率变大。最大视距位置,即Hc=0 处(本算例中5 093m 处)是第二处拐点,从该位置之后进入超视距,只剩下球形月面绕射传播,斜率变得更大。基于S EKE算法建立的光滑月表传播模型,路经损耗也有两处拐点。第一处为Hc/F1=1 的位置(本算例中约33m 处),之前主要考虑自由空间传播损耗和反射多径损耗。由仿真结果可知,反射多径损耗在±1.6dB 之间浮动(见图5),对传播总损耗的影响非常微弱,因此从图4曲线来看,Hc/F1＞1时,传播总损耗近似等于自由空间损耗,0.5 ＜Hc/F1＜1时,除自由空间损耗以外的传播损耗,由多径干涉损耗和球形月面绕射损耗加权计算得出,斜率增大(由于该距离段内的相对余隙值变化较其他距离段快,该阶段损耗变化斜率也最大)。第二处拐点为Hc/F1=0.5 的位置(本算例中约133m 处),之后第一费涅尔区遮挡严重,不再考虑反射多径影响,而主要考虑球形月面绕射影响。

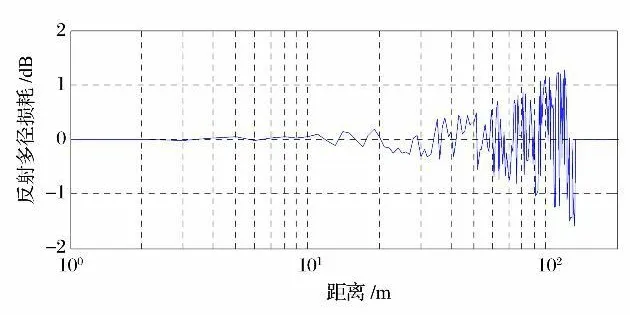
图5 反射多径损耗Fig.5 Multipath loss

图6给出了两种模型计算结果差值随距离变化的曲线。可以看出,两种传播模型计算结果在收发距离较小(Hc/F1＞1时,本算例中约33m 以内)或收发距离较大(Hc/F1＜0时,即超视距,本算例中约5 093m 以外)的情况下,计算结果基本相同,前者近似为自由空间传播,后者为球形月面绕射传播。在(33m,5 093m)时,SEKE算法得出的损耗计算结果,大于基于标准算法建立的模型得出的损耗计算结果,两种模型计算结果最大差值约为48dB(Hc/F1=0.5 处,本示例中约133m 处)。这是由于所用计算的绕射数学模型不同造成的,采用球形月面绕射模型计算的损耗绝对值,比采用圆表障碍物绕射模型计算的结果大。随着距离越来越大,计算结果的差别也越来越小,这与圆表障碍物绕射模型越来越接近球形月面绕射模型的情况是一致的。

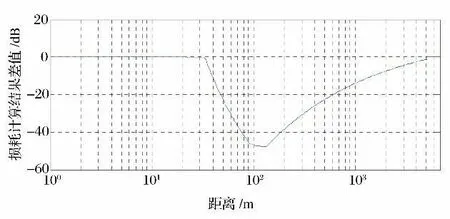
图6 两种传播模型的计算结果差值Fig.6 Differential value of calculation results for two models

由于本文所建立的两种传播模型对月表电波传播特性模拟的精确性,还无法在地面上进行验证,因此暂时无法给出两种模型的优劣性判断。但是,从仿真结果可以看出,当通信距离达到一定的长度,两种传播模型计算结果的差值将大大缩小,并在最大直视距离以外达到一致。本算例中,当收发距离超过约1 500m 之后,两种模型的损耗计算结果差值缩小到10dB 以内,超过约3 000m 之后,差值缩小到5dB 以内。从仿真结果可知,两种传播模型的计算结果在变化趋势上是一致的。对工程设计而言,可根据月面通信的最大设计距离,通过调整发射天线和接收天线的高度、载波频率等参数,对两种传播模型的计算结果综合考虑,在工程可实现的前提下,尽量避免或降低绕射损耗的影响,从而给出最优设计参数。

4 结束语

本文以探月工程中着陆器与月面巡视器之间的月表通信的特殊环境为应用背景,对几种基本电波传播模型在月表的应用条件进行了分析,分别建立了基于标准多径干涉和绕射算法以及基于SEKE算法的光滑月表无线电波传播模型,并应用一个仿真示例对两种模型的仿真结果进行了分析比较。无论采用哪种算法,对VHF 或UHF频段而言,沿光滑月表的绕射传输损耗都非常严重,在工程设计中,应尽量避免或降低绕射损耗的影响。本文建立的两种月表无线电波传播模型,可为实际工程设计提供仿真分析工具,仿真结果可作为工程设计的参考依据,此建模方法也同样适用于火星、金星探测任务中的着陆器与巡视器之间通信链路的设计。

References)

[1]Serpil A.S EKE:a computer model for low altitude radar propagation over irregular terrain[J].IEEE Transactions on Antennas and Propagation,1986,34(8):1013-1023

[2]David AS.Generalized radar clutter model[J].IEEE Transactions on Aerospace and Electronic systems,1999,35(3):857-865

[3]苏玉瑞,吴彦鸿,刘鹏军,等.复杂地形环境中电磁波多径传输建模与仿真[J].舰船电子工程,2009,29(1):168-172

[4]王全民,张卫华,郭刚,等.综合射频环境效应仿真及其在JMASE 中的实现[J].计算机仿真,2006,23(9):49-57

[5]ITU-R.ITU-R Rec.P.526-5 propagation by diffraction[S].Geneva:ITU,2003

[6]刘以安,邓亮,钟娟,等.雷达电磁信号的多径传播仿真研究[J].计算机仿真,2005,22(6):15-19

[7]CCIR.Report 715-3,Rec.and Rep.of CCIR,5 propagation by diffraction[S].Geneva:ITU,1990

[8]Kerr D E.Propagation of short radio w aves.radiation laboratory series[M].New York:McGraw Hill,1951

[9]杰里·L·伊伏斯,爱德华· K·里迪.现代雷达原理[M].卓荣邦,等译.北京:电子工业出版社,1991

[10]Zhang Wenxun.An improved zoning rule of the Fresnel zone plate[J].Microw ave Opt Technol Lett,1999,23(2):69-73