Optimal Upper and Lower Bounds for Logarithmic Mean*

HOU Shou-w ei ,XU Yan-w u ,CHU Yu-ming

(1.Department of Mathematics,Hangzhou Normal University,Hangzhou 310012,China;2.School of Economics,Shanghai University of Finance and Economic,Shanghai 200433,China;3.Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

Optimal Upper and Lower Bounds for Logarithmic Mean*

HOU Shou-w ei1,XU Yan-w u2,CHU Yu-ming3

(1.Department of Mathematics,Hangzhou Normal University,Hangzhou 310012,China;2.School of Economics,Shanghai University of Finance and Economic,Shanghai 200433,China;3.Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

M aking use of elementary differential calculus,we compare the logarithmic mean w ith the convex combination of root-square and harmonic root-squaremeans,and find the greatest valueαand the least valuesβsuch that the double inequalityholds fo r all a,b＞0 w ithare the rootsquare,harmonic root-square,and Logarithmic meansof two positive numbers a and b,w ith a≠b,respectively.

root-squaremean;harmonic root-squaremean;Logarithmic mean

MSC 2000:26E60 26D20

0 In troduction

Fo r p∈R,the p-th pow er mean Mp(a,b)and logarithm ic mean L(a,b)of two positive num bers a and b is defined by respectively.

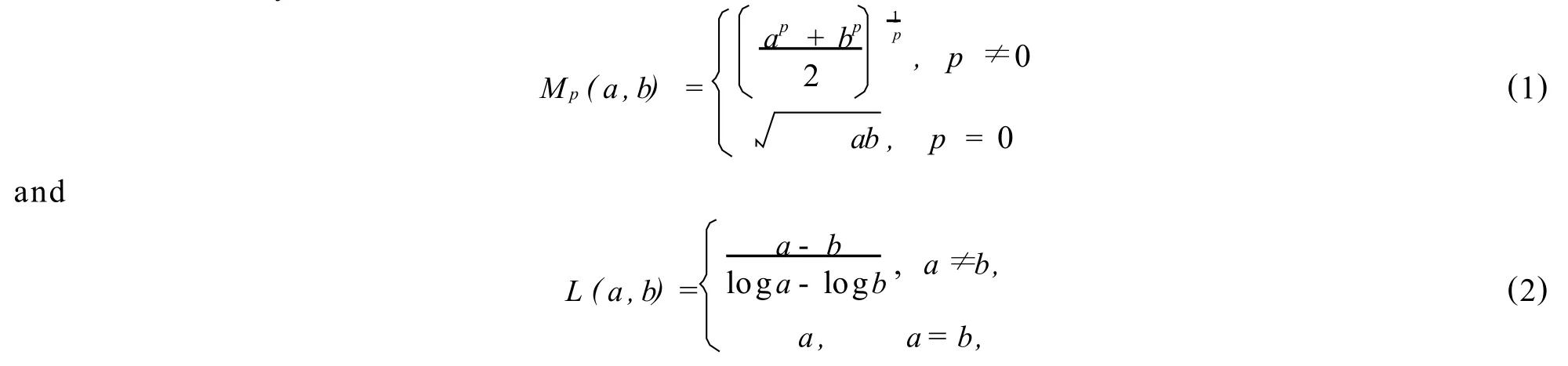
Recently,both mean values have been the subject of intensive research.In particular,many remarkable inequalities for Mp(a,b)and L(a,b)can be found in the literature[1～17].It iswell know n that Mp(a,b)is continuous and strictly increasing w ith respect to p∈R fo r fixed a,b＞0 w ith a≠b,and many means are special cases of the power mean,for examp le,

are the harmonic root-square,harmonic,geometric,arithmetic,and root-square means of a and b,respectively.

Lin[13]p resent the op timal double inequality

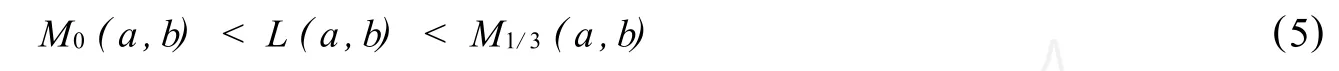
fo r all a,b＞0 w ith a ≠b.

In[6],Long and Chu answer the question:w hat are the greatest value p=p(α,β)and least value q=q(α,β)such that the double inequality

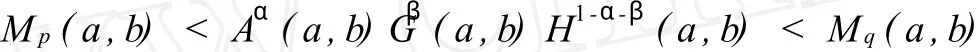
holds fo r all a,b＞0 w ith a≠b andα,β＞0 w ithα+β＜1?

The follow ing sharp bounds for the combination of arithmetic and logarithmic means in term s ofpower mean are given in[7]:

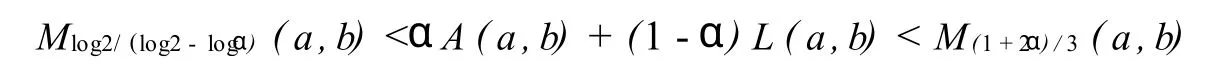
fo r allα∈(0,1)and a,b＞0 w ith a ≠b.

The main purpose of thispaper is to answer the question:w hat are the greatest valueαand least valueβsuch that the double inequality

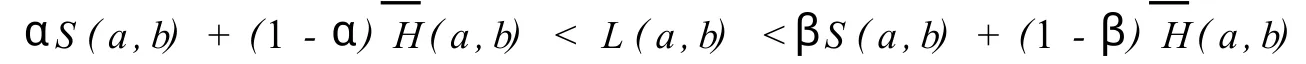
holds fo r all a,b＞0 w ith a≠b.

1 Lemma

In order to establish our main result we need a lemma,w hich we p resent in this section.

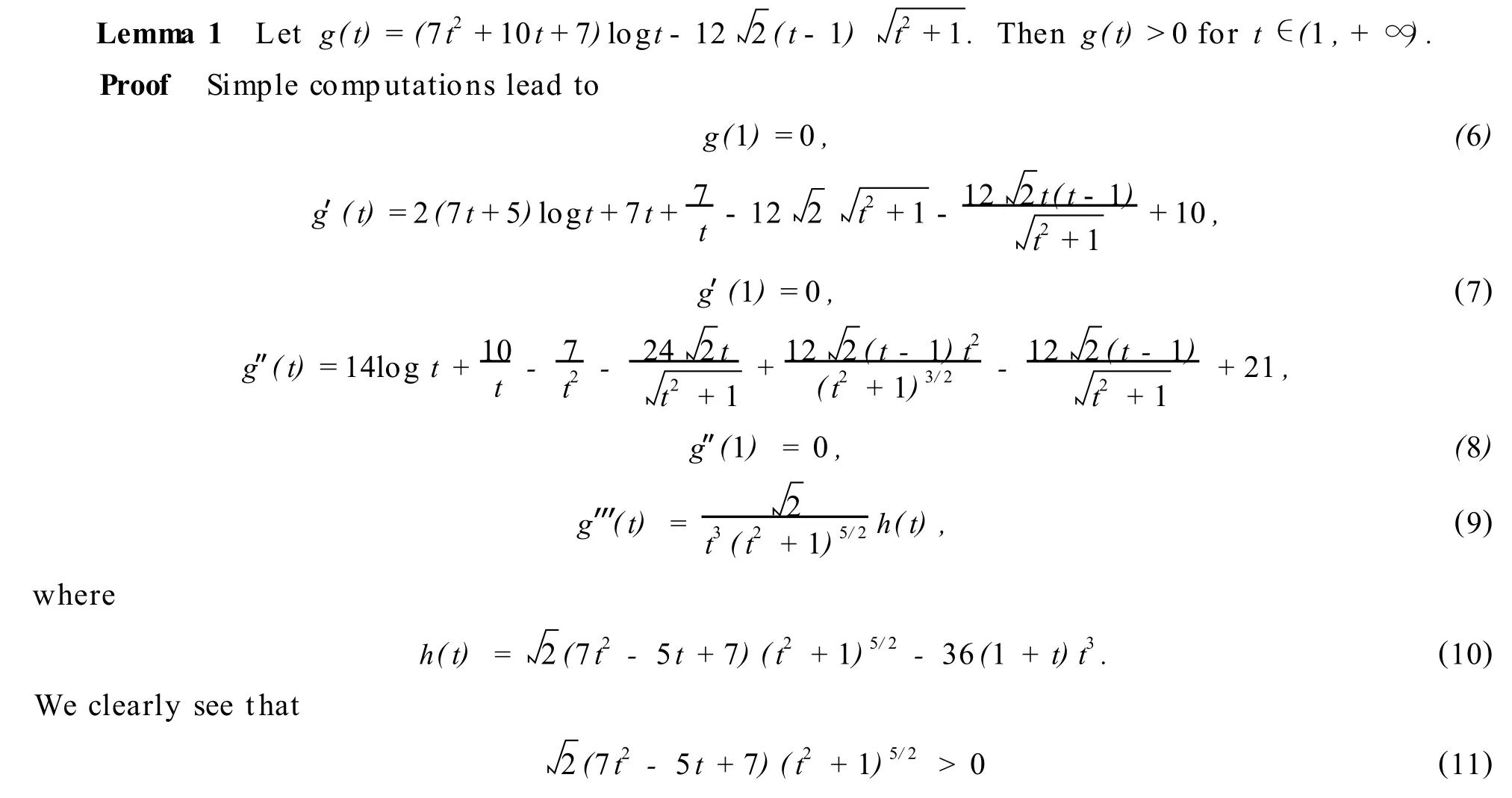
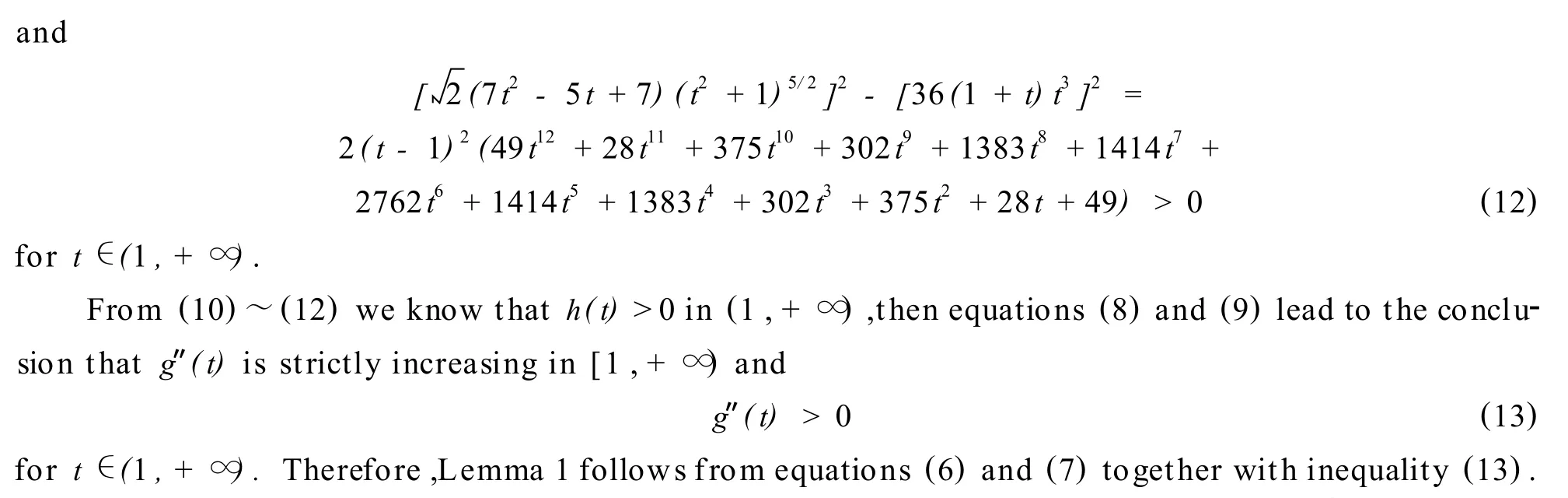
2 Main Result

[1]SH IM Y,CHU Y M,JIANG Y P.Op timal inequalities among varousmeansof two arguments[J].Abstr Appl Anal,2009,2009:1～10.

[2]SH IM Y,CHU Y M,JIANG Y P.Three best inequalities fo r means[J].Int Math Fo rum,2010,5(22):1059～1066.

[3]CHU Y M,XIA W F.Two sharp inequalities fo r powermean,geometricmean,and harmonicmean[J].J Inequal App l,2009,2009:1～6.

[4]CHU YM,XIA W F.Inequalities for generalized logarithmic means[J].J Inequal Appl,2009,2009:1～7.

[5]LONGB Y,CHU Y M.Op timal inequalities for generalized logarithmic,arithmetic,and geometric means[J].J Inequal App l,2010,2010:1～10.

[6]LONGB Y,CHU Y M.Op timal powermean bounds for the weighted geometric mean of classicalmeans[J].J Inequal App l,2010,2010:1～6.

[7]XIA W F,CHU Y M,WANG GD.The op timal upper and lower power mean bounds for a convex combination of the arithmetic and logarithmic means[J].Abstr Appl Anal,2010,2010:1～9.

[8]CHU Y M,LONGB Y.Best possible inequalities between generalized logarithmic mean and classicalmeans[J].Abstr App l Anal,2010,2010:1～13.

[9]CHU Y M,XIA W F.Two op timal double inequalities between power mean and logarithmic mean[J].Comput Math App l,2010,60(1):83～89.

[10]LONGB Y,XIA W F,CHU YM.An op timal inequality for powermean,geometric mean and harmonic mean[J].Int J Mod Math,2010,5(2):149～155.

[11]CHU Y M,Q IU Y F,WANG M K.Sharp power mean bounds fo r the combination of Seiffert and geometric means[J].Abstr Appl Anal,2010,2010:1～12.

[12]Wang M K,Chu Y M,Qiu Y F,et al.An op timal power mean inequality for the comp lete ellip tic integrals[J].App l Math Letters,2011,24:887～890.

[13]L IN T P.The power and the logarithmic mean[J].Amer Math Monthly,1974,81:879～883.

[14]STOLARSKY K B.The power and generalized logarithmic means[J].Amer Math Monthly,1980,87(7):545～548.

[15]IMORU C O.the power mean and the logarithmic mean[J].Internat J Math Math Sci,1982,5(2):337～343.

[16]BURK F.The geometric,logarithmic,and arithmetic mean inequality[J].Amer Math Monthly,1987,94(6):527～528.

[17]ALZER H,Q IU SL.Inequalities for means in two variables[J].A rch Math,2003,80(2):201～215.

MSC 2000:26E60 26D20

对数平均的最佳上下界

候守伟1,徐言午2,褚玉明3

(1.杭州师范大学数学系,浙江杭州310012;2.上海财经大学经济学院,上海200433;3.湖州师范学院理学院,浙江湖州 313000)

利用初等微分学比较了对数平均与平方根平均和调和平方根平均的凸组合,发现了使得双向不等式αS(a,b)+(1对所有 a,b＞0且 a≠b成立的α的最大值和β的最小值,其中 S(a,b)分别表示二个正数 a与b的平方根平均、调和平方根平均和对数平均.

平方根平均;调和平方根平均;对数平均

O174.1

O174.1 Document code:A Article ID:1009-1734(2011)01-0007-04

date:2011-01-21

s:This research is suppo rted by the Natural Science Foundation of China(11071067)and the Innovation Team Foundation of the Department of Education of Zhejiang Porvince(T200924).

Biography:Hou Shou-wei,Postgraduate student of grade 2009,Department of Mathematics,Hangzhou Normal U-niversity,Research Interest:Comp lex Analysis.