湍流普朗特数识别的随机抽样算法

朱 嵩，刘国华，程伟平，黄跃飞

湍流普朗特数识别的随机抽样算法

朱 嵩1，刘国华2，程伟平2，黄跃飞3

（1.广东省电力设计研究院水务部，广州 510663；2.浙江大学建筑工程学院，杭州 310058；3.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

在温排水等涉及热交换的环境水力学研究中，湍流普朗特（Prandtl，简称Pr）数是控制温度的主要参数。对于一个特定的问题，传统湍流Pr数的确定方法主要采用经验法或试错法，因而具有一定盲目性和低效性。为了提高湍流Pr数确定的可靠性，采用马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，简称MCMC）随机抽样的方法（Metropolis-Hastings算法）来对湍流Pr数进行识别，其中湍流场计算采用了稳态标准k-ε模型，温度场计算采用非稳态热传导方程。算例计算结果表明，MCMC方法对湍流Pr数的识别具有良好的适用性和较高的识别精度。

湍流Prandtl数；参数识别；湍流传热；Metropolis-Hastings算法；MCMC随机抽样

1 概 述

在电厂的水工工艺设计过程中，需要解决大量的湍流传热问题。如湿冷塔内的水气两相换热、空冷平台热交换等。此类问题的主要特征是换热与湍流流动的耦合，属于湍流扩散的研究范畴。湍流扩散遵循着质量守恒、动量守恒和能量守恒方程，可以采用广义对流扩散方程描述。要准确获得湍流热扩散中的温度场，关键是要确定湍流热扩散系数。研究已经表明，湍流涡黏性系数与湍流热扩散系数之比为一常数，称为Prandtl（Pr）数。不同流动下的湍流Pr数是不同的，一般根据流动的类型经验加以确定，或通过手工调节的方法和观测值对比从而找到当前流动的湍流Pr数。前一种方法，由于湍流Pr数的范围仍然较大，选择起来仍然具有主观性；后一种虽然通过试验结果加以率定，但手工调节的方式费时费力。

目前，优化算法、人工智能等方法已广泛应用于相关的环境水力学反问题研究中［1］，如遗传算法［2，3］、模拟退火算法［4］以及贝叶斯方法［5－9］等。由于贝叶斯方法的先验、后验概念以及马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）的强大后验分布抽样能力，使得该方法近年来获得了飞速的发展和广泛的应用。相比较优化算法而言，MCMC方法能获得整个参数的后验分布信息。相比较人工神经网络等黑箱模型而言，贝叶斯MCMC方法具有明确的数学理论指导。

由于传热传质问题的类比性，在湍流传热传质研究过程中，Schmidt数和Pr数在一些场合下并不区分，实指同一含义［9］。Yoshihide Tominaga和Ted Stathopoulos调查总结了射流、浊流、边界层羽流弥散和建筑物附近的流动中的湍流Schmidt数的经验取值，指出湍流Schmidt数对预测结果具有较大的影响，应该根据不同类型的流动具体地加以研究［10］。Yanhu Guo等人采用遗传算法（Genetic Algorithm，GA）估计了横流中射流变系数Schmidt数，取得了较好的结果［11］。

采用贝叶斯方法以及MCMC抽样解决传热学方面的文献可参见文献［12－14］，但目前尚未见贝叶斯MCMC方法在湍流传热反问题研究上的应用。本文采用Metropolis-Hastings算法对湍流Pr数进行了识别研究。湍流传热物理场耦合场的求解采用有限单元法计算，其中湍流场采用稳态标准k-ε模型求解，温度场采用非稳态热传导方程求解。采用的二维湍流热扩散的算例计算表明贝叶斯MCMC方法能够较好地识别湍流传热过程中的Pr数。

2 湍流传热数学模型

本文采用非稳态热传导方程描述热扩散现象，其中湍流流速场采用k-ε模型求解，控制方程如下：

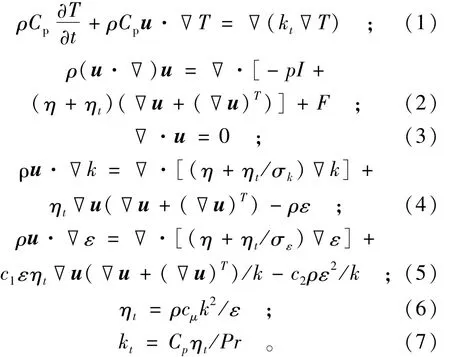
式中：ρ为密度；Cp为热容；T为温度；u为流速矢量；kt为湍流热扩散系数；p为压强；η为流体动力黏度；ηt为湍流运动黏度；c1，c2，cμ，σk和 σε为标准k-ε模型的5个参数；Pr为湍流Prandtl数。

3 贝叶斯推理与MCMC抽样方法

3.1 贝叶斯定理和反问题

贝叶斯推理的基础是贝叶斯定理，它可以表述如下

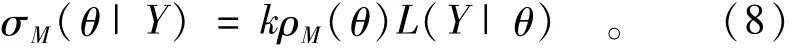
式中：θ，Y分别为模型参数和观测数据；ρM（θ），L（Y｜θ），σM（θ｜Y）分别为模型的先验概率密度函数，似然函数和后验概率密度函数；ρM（θ）表示在未收集到数据之前关于参数的认识，它主要来源于以往的观测资料、经验和主观判断等；L（Y｜θ）表示模型参数拟合实测数据的程度，值越大表明拟合程度越好，反之则差；σM（θ｜Y）即为反问题的解，它表示在获得观测数据之后模型参数的分布规律。

3.2 抽样方法

一旦获得了参数的后验分布，就可以获得参数的具体特征，如单个参数的边缘分布或均值、方差等。但对于很简单的情况，后验概率分布都不能以解析解的形式给出，所以必须采用数值积分方法。马尔可夫链蒙特卡罗（MCMC）就是一种对复杂问题在高维空间上的数值积分方案。它的主要思路就是创造一个随机游动（马尔可夫过程）使得后验概率密度函数σM（θ｜Y）作为它的静态分布，只要这个计算过程愈长，那么采样结果就愈服从后验概率分布。

构造马尔可夫链的方法很多，主要包括Gibbs采样，Metropolis（Metropolis-Hasting）算法等。本文采用Metropolis算法对模型参数后验分布进行采样，算法如下：

（1）给定参数的初始点 θ（0）；

（2）在当前模型参数θ（t）的状态下给定一个随机的无偏扰动，从而生成一个新的状态θ′，计算出似然函数 L（θ（t））和 L（θ′）；

（3）生成［0，1］间均匀分布的随机数U；

（4）如果 L（θ′）≤L（θ（t））或则接受θ′，否则拒绝，转到（2）直到预定的次数。

4 算例计算

4.1 算例一

假设在0.9 m×0.25 m的矩形域如图1内存在一水体的湍流传热过程，流场和温度场的计算采用稳态标准k-ε模型和非稳态热传导方程。采用有限元法离散计算，计算域共剖分了2 800个四边形网格，采用二次形函数。边界条件设置如表1。进口流速为1 m／s、进口湍流强度为5%，进口温度为343.15 K，初始温度为293.15 K，水的热容为 4 182J×kg×K－1。湍流模型参数取值如表2。

图1 计算域Fig.1 Computational domain

表1 边界条件设置Table 1 Setting of the boundary condition

表2 标准k-ε湍流模型参数取值Table 2 Values of standard k-εturbulence model

为了考查MCMC算法对该问题的适用性，预设湍流Pr数的真值为0.8，通过后验分析来验证贝叶斯MCMC参数识别的精度。在距离进口0.5 m处的对称轴上设置一测点 O。取 O点上 0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9以及 1 s时 11个时刻上的温度值作为观测数据，如图2所示。

考虑到湍流Pr数几乎对湍流场没有影响，因而识别过程中只计算一次湍流场，而反复调用温度场求解模型。设计的湍流Pr数识别的流程如下：

（1）根据几何生成有限元网格；

（2）根据流场的参数及边界条件计算得到湍流场，为标量场的计算提供背景；

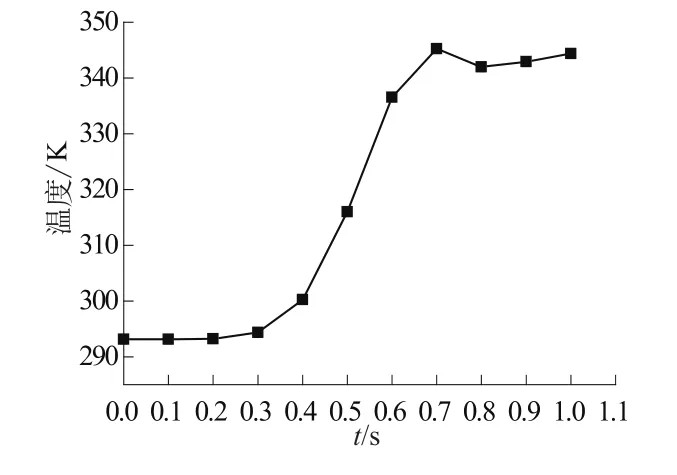
图2 测点O上的温度观测值Fig.2 Measured temperature at point O

（3）在先验范围内产生湍流Pr数的初值，计算似然函数，采用Metropolis-Hastings算法产生湍流Pr数的后验样本；

（4）对后验样本进行统计来识别未知湍流Pr数。

MCMC参数设置如下：Pr数的先验范围为［0.2，1.0］，先验分布为均匀分布。似然函数构造基于温度噪声为白噪声N［0，σ2］，其中 σ假设为0.1。随机游走的步长为先验范围的5%，迭代次数为100次。

湍流Pr数的迭代曲线如图3所示。可见，MCMC迭代在经历过约20步初始化阶段后，进入了统计收敛区域，主要表现为围绕真值0.8上下小幅震荡。图4为湍流Pr数的后验统计结果。从图中可以看出，湍流Pr数的后验概率在真值0.8附近出现的概率最高，符合预设的判断。表3为后验统计结果，从表3中可以看出，后验均值和后验中位数均具有较高的识别精度。

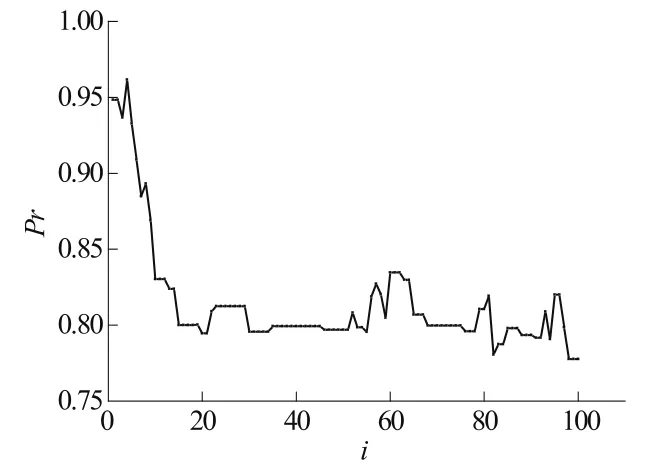
图3 湍流Pr数迭代曲线Fig.3 Iteration curve of turbulent Pr number

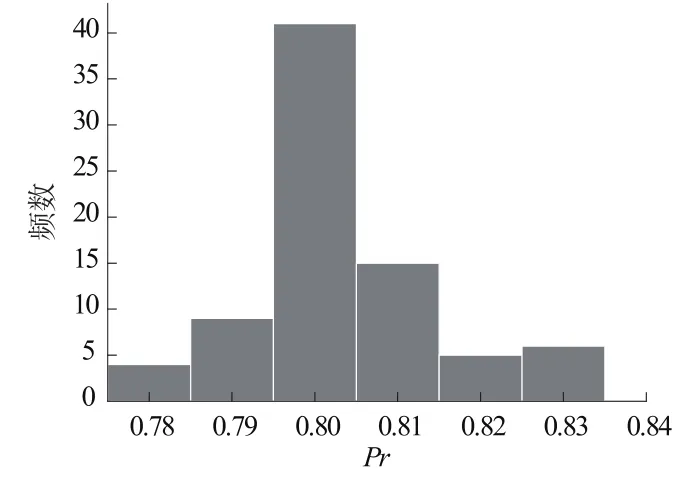
图4 湍流Pr数的后验分布Fig.4 Posterior distribution of turbulent Pr number

表3 湍流Pr数后验统计结果Table 3 Posterior results of turbulent Pr number

4.2 算例二

在一个0.889 m×0.304 8 m的二维计算域中有一横流中射流（Jet in Crossflow），射流小孔长度为0.025 4 m，射 流 流 速 为 2.3 m／s，射 流 温 度 为293.15 K；横 流 流 速 为 1 m／s，横 流 温 度 为283.15 K，流动介质为水。假设湍流Pr数为1。有限元计算考虑温度对水的密度及热容的影响，流场方程和温度场方程进行耦合求解。计算得到的温度场如图5所示。

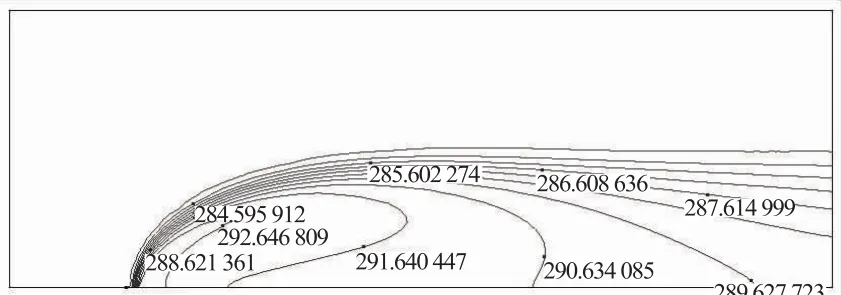
图5 射流温度场分布（单位：K）Fig.5 Temperature field of jet flow（Unit in K）

测 点 布 置 在 （0.5，0.05），（0.5，0.1），（0.5，0.15），（0.5，0.2）和（0.5，0.25）5个位置，通过有限元计算得到测点上的温度值分别为291.148 9 K，290.506 1 K，283.860 3 K，283.150 4 K和283.150 0 K。

MCMC参数设置如下：湍流Pr数的先验范围为［0.2，1.0］，先验分布为均匀分布。似然函数为拉普拉斯函数，标准差为0.1。随机游走的步长为先验范围的5%，迭代次数为1 000次。

湍流Pr数的迭代曲线如图6所示。可见，MCMC迭代在经历过约100步初始化阶段后，进入了统计收敛区域，主要表现为围绕真值1.0上下小幅震荡。图7为湍流Pr数的后验统计结果。从图中可以看出，湍流Pr数的后验概率在真值1.0附近出现的概率最高，符合预设值。

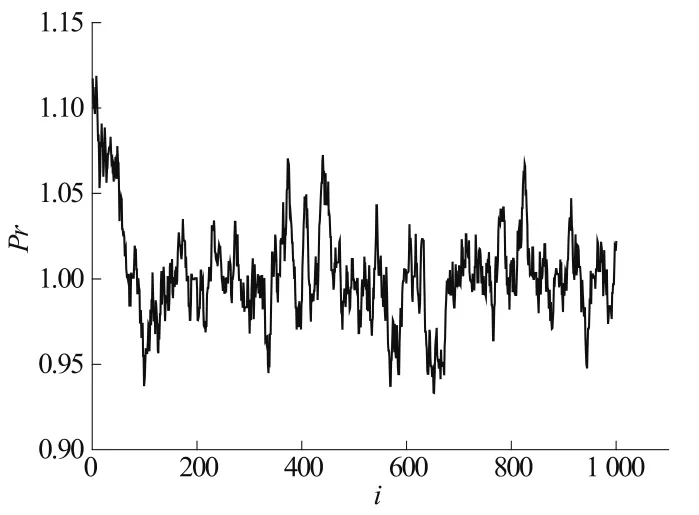
图6 湍流Pr数迭代曲线Fig.6 Iteration curve of turbulent Pr number

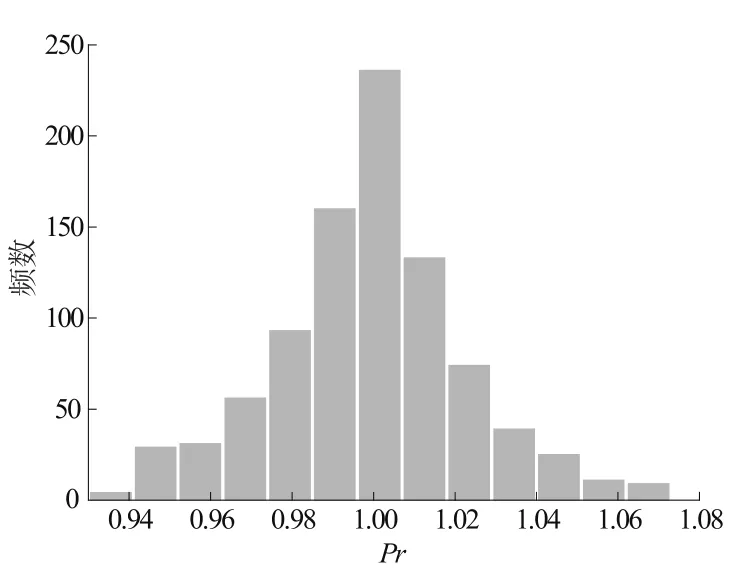
图7 湍流后验Pr数的后验分布Fig.7 Posterior distribution of turbulent Pr number

5 结论与展望

湍流普朗特数是控制湍流扩散中温度分布的关键参数，本文采用一种马尔科夫链蒙特卡罗方法Metropolis-Hastings算法对湍流稳态传热和非稳态传热两种典型模型进行了参数识别。其中，湍流求解采用了标准k-ε模型，离散方法采用了通用性较强的有限元法。计算结果表明，基于Metropolis-Hastings算法的湍流普朗特数识别能够达到较高的精度。

计算中的数据采用湍流时均值，考虑脉动测量值以及高级湍流模型的关键参数识别是需要进一步研究的课题。

［1］ 刘晓东，姚 琪，薛红琴，等.环境水力学反问题研究进展［J］.水科学研究进展，2009，20（6）：885－893.（LIU Xiao-dong，YAO Qi，XUE Hong-qin，et al.Advance in Inverse Problems of Environmental Hydraulics［J］.Advances in Water Science，2009，20（6）：855－893.（in Chinese））

［2］ NG A W M，PERERA B JC.Selection of Genetic Algorithm Operators for River Water Quality Model Calibration［J］.Engineering Applications of Artificial Intelligence，2003，16（5－6）：529－541.

［3］ 朱 嵩，毛根海，刘国华.基于FVM-HGA的河流水质模型多参数识别［J］.水力发电学报，2007，26（6）：91－95.（ZHU Song，MAOGen-hai，LIU Guo-hua.Parameters Identification of River Water Quality Model Based on Finite Volume Method-Hybrid Genetic Algorithm［J］.Journal of Hydroelectric Engineering，2007，36（6）：91－95.（in Chinese））

［4］ 王 薇，曾光明，何 理.用模拟退火算法估计水质模型参数［J］.水利学报，2004，（6）：61－67.（WANG Wei，ZENG Guang-ming，HE Li.Estimation of Water Quality Model Parameters with Simulated Annealing Algorithm［J］.Journal of Hydraulic Engineering，2004，（6）：61－67.（in Chinese））

［5］ 朱 嵩，毛根海，程伟平，等.利用贝叶斯推理估计二维含源对流扩散方程参数［J］.四川大学学报（工程科学版），2008，40（2）：38－43.（ZHU Song，MAO Genhai，CHENG Wei-ping，et al.Application of Bayesian Inference to Estimate the Parameters in 2D Convection-Diffusion Equation with Source［J］.Journal of Sichuan University（Engineering Science Edition），2008，40（2）：38－43.（in Chinese））

［6］ 朱 嵩，毛根海，刘国华，等.改进的MCMC方法及其应用［J］.水利学报，2009，40（8）：1019－1023.（ZHU Song，MAO Gen-hai，LIU Guo-hua，et al.Improved MCMC Method and Its Application［J］.Journal of Hydraulic Engineering，2009，40（8）：1019－1023.（in Chinese））

［7］ 朱 嵩，刘国华，王立忠.水动力-水质耦合模型污染源识别的贝叶斯方法［J］.四川大学学报（工程科学版），2009，41（5）：30－35.（ZHU Song，LIU Guo-hua，WANG Li-zhong.A Bayesian Approach for Identification of the Pollution Source in Water Quality Model Coupled with Hydrodynamics［J］.Journal of Sichuan University（Engineering Science Edition），2009，41（5）：30－35.（in Chinese））

［8］ 朱 嵩.基于贝叶斯推理的环境水力学反问题研究［D］.杭州：浙江大学，2008.（ZHU Song.Research on Inverse Problems of Environmental Hydraulics by Bayesian Inference［D］.Hangzhou：Zhejiang University，2008.（in Chinese））

［9］ 朱 嵩.湍流标量输运过程中关键参数的识别研究［R］.杭州：浙江大学，2010.（ZHU Song.Study on the Identification for Key Parameters of the Scalar Transport Process in the Turbulence［R］.Hangzhou：Zhejiang University，2008.（in Chinese））

［10］TOMINAGA Y，STATHOPOULOST.Turbulent Schmidt Numbers for CFD Analysis with Various Types of Flowfield［J］.Atmospheric Environment，2007，41（37）：8091－8099.

［11］GUO Yan-hu，HE Guang-bin，ANDREW T H.Application of Genetic Algorithms to the Development of a Variable Schmidt Number Model for Jet-in-crossflows［J］.International Journal of Numerical Methods for Heat＆Fluid Flow，2007，11（8）：744－761.

［12］WANG Jing-bo，ZABARASN.Using Bayesian Statistics in the Estimation of Heat Source in Radiation［J］.International Journal of Heat and Mass Transfer，2005，48：15－29.

［13］WANG Jing-bo，ZABARASN.A Markov Random Field Model of Contamination Source Identification in Porous Media Flow［J］.International Journal of Heat and Mass Transfer，2006，49：939－950.

［14］LING L，YAMAMOTO M，HON Y C，et al.Identification of Source Locations in Two-Dimensional Heat Equations［J］.Inverse Problems，2006，22：1289－1305.

A Random Sampling Algorithm for Identification of Turbulent Prandtl Number

ZHU Song1，LIU Guo-hua2，CHENG Wei-ping2，HUANG Yue-fei3
（1.Water Engineering Department，Guangdong Electric Power Design Institute，Guangzhou 510663，China；2.College of Civil Engineering and Architecture，Zhejiang University，Hangzhou 310058，China；3.State Key Laboratory of Hydroscience and Engineering，Tsinghua University，Beijing 100084，China）

Turbulent Prandtl number（Pr）is a key parameter for controlling the temperature distribution in the research of thermal discharge water and other environmental hydraulics involving heat transfer.For a given problem，turbulent Pr number generally comes from previous experiences or trial-and-error method，which is blindfold and inefficient.To increase the reliability of turbulent Pr number for a given problem，Metropolis-Hastings algorithm，a Markov Chain Monte Carlo（MCMC）random sampling method was employed in this paper to identify turbulent Pr number.In the numerical simulation，steady standard k-εmodel was used for turbulence flow field computation，while unsteady heat transfer equation was adopted for computing the temperature field.The computation results manifested that MCMCmethod is suitable and can offer precise results for the identification of turbulent Pr number.

turbulent Prandtl number；parameter identification；turbulent heat transfer；Metropolis-Hastings algorithm；MCMC random sampling

O242.28，O357.5＋3

A

1001－5485（2011）06－0016－04

2010-07-01

国家重点基础研究计划资助项目（2005CB724202）；国家自然科学基金资助项目（50879075）

朱 嵩（1981-），男，安徽颍上人，博士后，工程师，从事计算流体力学和电厂水工工艺研究，（电话）020-32117746（电子信箱）zhusong＠gedi.com.cn。

（编辑：王 慰）