材料腐蚀疲劳寿命估算方法探讨
姚新华,何耀辉
(中海油深圳分公司惠州油田,广东 深圳 518067)
材料腐蚀疲劳寿命估算方法探讨
姚新华,何耀辉
(中海油深圳分公司惠州油田,广东 深圳 518067)
在总结国内外估算腐蚀疲劳寿命研究成果的基础上,给出了估算材料腐蚀疲劳寿命的三种方法及其优缺点.解析法主要基于经验公式和实验确定的一些常数来计算材料在腐蚀疲劳环境下的寿命.能量法是从材料的微观结构来研究材料失效的机理,从导致材料失效发生的晶体间的破坏而产生能量耗散的角度研究材料腐蚀疲劳寿命.实验法主要通过模拟实验得出实际服役情况下材料的腐蚀疲劳寿命,但是该方法在再现性较差情况下存在诸多不确定因素.
疲劳寿命估算;腐蚀疲劳;解析法;能量法;实验法
材料腐蚀疲劳的研究在国内起步较晚,因此对于材料腐蚀疲劳寿命的研究还不够深入.在设计工程构件时,由于对腐蚀疲劳寿命研究不足,而导致构件提前失效的事件屡见不鲜.随着工程构件在各种复杂环境下疲劳破坏问题的日益突出,腐蚀疲劳寿命的研究显得越来越重要.目前,国内对腐蚀疲劳寿命的研究尚处于发展阶段.
从研究常规材料疲劳寿命的观点来看,腐蚀疲劳寿命Nf的研究分为:腐蚀疲劳裂纹的形成期Ni和腐蚀疲劳裂纹的扩展期Np,表示为:Nf=Ni+Np.关于腐蚀疲劳寿命的估算方法大致有:解析法、能量法和实验法.
1 解析法
对腐蚀疲劳寿命研究最深入的领域当属航天、航空.在航天、航空特定的环境下,估算材料腐蚀疲劳寿命的方法有经验公式,而对于一般材料腐蚀疲劳寿命的两个阶段有不同的解析表达式.
腐蚀疲劳裂纹形成期的解析表达式[1]为:
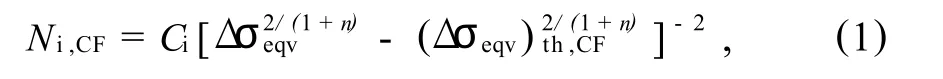
式(1)中:Ci—腐蚀疲劳裂纹形成起始抗力系数;n—材料的应变硬化指数;Δσeqv—当量应力幅;(Δσeqv)th,CF—形成腐蚀疲劳裂纹门槛的当量应力幅.
腐蚀疲劳裂纹形成起始抗力系数Ci是一个对腐蚀介质不敏感的材料常数,可根据疲劳裂纹起始的力学模型近似计算确定.疲劳载荷下腐蚀疲劳裂纹形成起始抗力系数与材料拉伸性能之间具有下列关系[2]:

式(2)中:σf—材料的断裂强度;εf—材料的断裂延性;E—材料的弹性模量;n—材料应变硬化指数.
腐蚀环境的影响区别于一般的空气环境,主要表现在形成腐蚀疲劳裂纹的门槛(Δσeqv)th,CF大为降低,一般通过试验方法测定(Δσeqv)th,CF.因此,只要知道材料的拉伸性能和特定环境下形成腐蚀疲劳裂纹的门槛值,便可计算出起始寿命.
腐蚀疲劳裂纹扩展期的研究是基于 Paris公式,但由于Paris公式的局限性,人们研究出一个比较符合工程实际的腐蚀疲劳裂纹扩展速率解析表达式[3]:

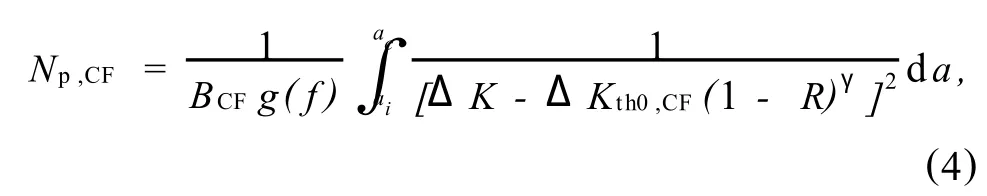
式(4)中的BCF,g(f),ΔKth0,CF,R,γ都很好确定,其关键就是积分上下限的确定.就积分下限而言,近30年来,很多研究者采用切口试件直接测定疲劳裂纹形成寿命Ni,CF,并将裂纹形成寿命定义为切口根部形成0.25 mm长的裂纹时所经历的应力循环数[3].因此,实际计算时可取ai=0.25mm.而积分上限可按照断裂力学中材料在实际服役状态下裂纹临界尺寸的方法确定.对于有气密性要求的构件,如果临界裂纹尺寸大于材料构件的实际几何尺寸,则积分上限优先选用材料构件的实际几何尺寸;对于没有气密性要求的构件,还需要考虑结构整体强度要求下的构件尺寸,最后进行综合比较给出积分上限ac的取值[4].
2 能量法
用能量的观点来研究腐蚀疲劳寿命,认为材料遭受疲劳失效服役的过程是一个能量耗散的过程.当经历一定周次的应力作用,材料发生疲劳裂纹的本质原因是材料晶体间键的破坏的宏观表现.键的破坏伴随着能量的释放,在断裂力学上归结为热激活断裂理论,这一理论是从微观机理出发研究热激活断裂的宏观规律,从这一思路出发为研究裂纹扩展开辟了另一条路径.
疲劳裂纹的扩展是裂纹尖端在循环应力场的作用下不断钝化(应力增强)和锐化(应力释放)的结果.根据位错动力学理论,应力场每循环一次的裂纹扩展量是由钝化位移控制的,它等于裂纹尖端在应力场每循环一次的位错数与Burgers矢量的乘积.这样,位错动力学理论对疲劳裂纹扩展速率的描述为[5]:

式(5)中:b—Burgers矢量;n*—裂纹尖端在应力场每循环一次的位错数.
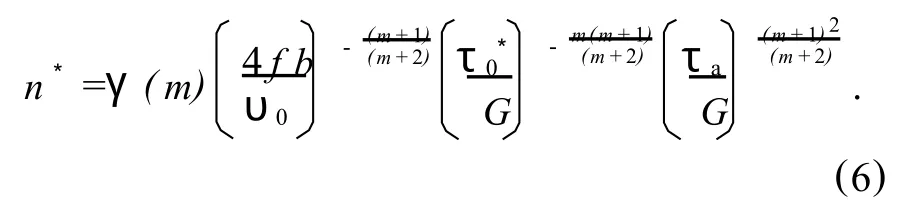
式(6)中m—位错速率方程υ=υ0=(τa/τ*0)m的指数;γ(m)—关于的m无量纲量,对于金属材料有 ,γ(m)=1.396m-1.45;τa—剪切应力;τ0*—位错速率;υ=υ0=10-2m/s所要求的应力值;G—材料切变模量;f—循环加载频率;
根据裂纹尖端的应力场,剪切应力τa和应力强度因子ΔK之间具有以下关系[6]:

式(7)中:ε—平均应力作用下的位移.
再根据热激活能理论和速率过程理论相关知识,可得疲劳裂纹扩展规律 Paris公式物理本质方程[7]:
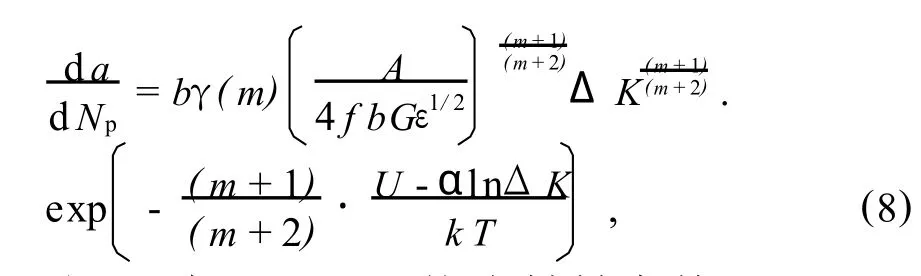
式(8)中A,U,α—均为材料常数;k—Boltzmann常数;T—温度.
方程(8)反映了材料疲劳扩展速率与加载频率和环境温度的关系,但还不能反映材料在腐蚀环境下的疲劳扩展速率.因此,欲计算出较精确的腐蚀疲劳扩展速率,还应考虑腐蚀环境条件的修正.
由热激活能理论知道,位错速率υ=Aexp(-Q/kT),其中Q=U-αlnΔK.由此可认为在腐蚀环境下,热激活能对加速构件破坏表现出了更大的功效.加上修正因子ζ,可得出新的位错速率υ*=ζAexp(-Q/kT),其中ζ主要由环境的腐蚀条件和金属材料两者共同决定.ζ>1表明,该金属材料在所设定的环境下腐蚀加剧;ζ<1表明,该金属材料所处的环境状况有利于金属的保护,进而推导出:
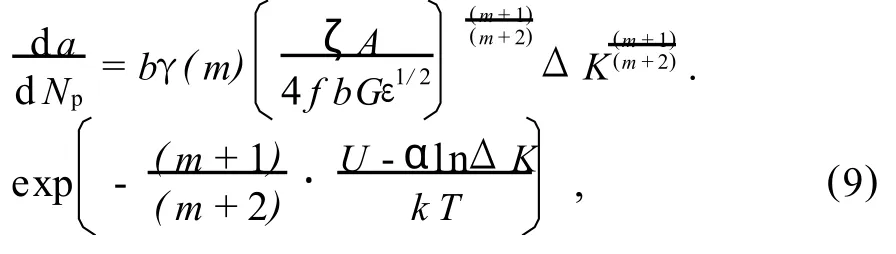
为了更深入理解上述问题,在此做出以下两个假设:
假设1:在材料受到交变载荷的作用下,要想使材料晶格产生错移,只有达到足够大的能量时才能使其发生晶格移动.因此,假定认为,循环加载的过程就是使晶格相互错移能量积蓄的过程,当能量积蓄到一定程度时,就发生晶格错移.微观上来看,晶格错移量很小时,可认为是疲劳破坏的裂纹萌芽期.这个假设就如同材料疲劳失效的临界应力值一样,即加载频率达到f>fth(即实际加载频率大于其加载的门槛值)时,材料才可能在连续加载情况下蓄积能量,发生疲劳裂纹扩展;当裂纹扩展后,蓄积的能量便被消耗,相当于对分裂金属键做功了.
假设2:材料在一定加载应力σ和加载频率f下发生疲劳失效,还应满足:H=h(σ,f)>Hth,即材料受到的加载应力和加载频率满足最小能量原理.因此,只有满足下述三个条件,材料才会发生疲劳失效.

式(10)中:H—材料受到的能量冲击;Hth—材料发生疲劳失效的最小能量;σ—材料受到的实际加载应力;f—材料受到的实际加载频率.σth—临界加载应力;fth—临界加载频率.
有了上面两个假设,便能更好地理解用能量法研究材料的腐蚀疲劳问题.如何知道实际情况是否同时满足以上两个假设呢?其实,根据材料试验得出的材料的S-N曲线有助于本问题的解决,当然上述假设的正确与否,或者说在特定情况下的正确与否还有待无数试验的进一步验证.
3 材料腐蚀疲劳寿命估算的实验法
实验法可以说是针对某一具体情况求解构件腐蚀疲劳寿命最好的方法.该方法针对具体问题,利用实验室条件或者根据实际情况人为事先对工程材料进行试验分析,得出一系列的实验分散数据点,最后通过曲线拟合得出材料的近似寿命曲线.还有就是通过疲劳实验机,直接获取疲劳寿命.这种方法的难点在于很难保证测试条件与材料的实际工作环境相一致,因为实际构件的服役状况是不可能像在疲劳实验机上那样经历高频率交变载荷,频率不同了,腐蚀速率和氢脆等自然就不一样.实验法对于那些再现性较好的情况具有很好的精度,但对于再现性差的情况则偏差可能较大.
4 结 论
对以上三种描述腐蚀疲劳寿命方法的研究表明:解析表达式法应该说最好用、最节约成本,而且是普遍采用的方法;不足之处就是运用解析表达式法时,必须首先知道材料的基本力学性能和拉伸性能以及不同腐蚀环境下该金属材料的腐蚀速率.能量法是通过微观的研究来表达宏观的现象,此方法应该是精度比较高的估算腐蚀疲劳寿命的方法,但碍于目前人们对能量法的研究不够深入,加之在用能量法求解时各物理量很难测量,因此推广性较差.实验法虽然是解决新材料腐蚀疲劳寿命问题必须采用的方法,但是往往是受实验条件或特殊要求的限制,有可能做出来的实验结果与事实偏差较大.因此,在分析材料构件的腐蚀疲劳寿命时优选解析表达式法,其次是实验法,再次考虑能量法.
[1]王荣,郑修麟,刘文宾.腐蚀疲劳裂纹起始的力学模型[J].固体力学学报,1995,16(S Issue):197-201.
[2]ZHENG Xiulin.A further study on fatigue crack initiation life-mechanical model fo r fatigue crack initiation[J].Int J Fatigue,1986,8(1):17-21.
[3]郑修麟.工程材料的力学行为[M].西安:西北工业大学出版社,2004.
[4]孙智,江利,应鹏展.失效分析-基础与应用[M].北京:机械工业出版社,2005.
[5]YOKOBORIT,YOKOBORIA T,KAM EIA.Dislocation dynamics theo ry fo r fatigue crack grow th[J].Int J of Fracture,1975,11(5):781-788.
[6]RICE J R.Dislocation nucleation from a crack tip:an analysis based on the peierls concep t[J].Journal of the Mechanics and Physics of Solids,1992,40(2):239-271.
[7]刘立名,段梦兰,柳春图,等.对裂纹扩展规律 Paris公式物理本质的探讨[J].力学学报,2003,35(2):171-175.
The study on estimating method of material corrosion fatigue life
YAO Xin-hua,HE Yao-hui
(Shenzhen B ranch H uizhou oil field CNOOC,Shenzhen 518067,China)
Based on the research results of corrosion fatigue life estimation at home and abroad,this paper p resents three kindsof solution methods for corrosion fatigue life estimation and discusses their advantages and disadvantages.Analyticalmethod ismainly based on empirical formulas and some constants from experiments to give out the calculated life under the co rrosion fatigue environment.Energy method is to study material failure mechanism from the microstructure of material,and to study material co rrosion fatigue life from the angle of energy dissipation caused by the intercrystalline failure leading to material failure.Experiment method is conducted mainly through simulation experiment,to obtain the corrosion fatigue life of materials under actual service conditions,however,w ith thismethod many uncertainties exist under poor rep roducibility.
fatigue life estimation;corrosion fatigue;analyticalmethod;energy method;experimentalmethod
1673-9981(2011)01-0045-04
TB303
A
收稿日期:2010-09-13
姚新华(1973—)男,河北石家庄人,工程师,学士.

