行为行星轨道假设下的社会作用力测度

杨华磊， 杨 林， 张维实

(1. 兰州大学 经济学院， 兰州 730000； 2. 兰州商学院 经贸学院， 兰州 730020)

目前，社会科学和自然科学不仅在研究方法上出现交叉和对称，而且在基础理论领域中出现趋同，正如《社会物理学》的主编牛文元所说：“统一承认物理世界和人文世界的随处呈现出来广义的‘差异’；统一承认广义的差异和非均衡必然导致广义的梯度；统一承认广义的梯度，必然要产生广义的力；统一承认广义的力的作用就必然产生广义的运动和广义的流；而探索广义的流和广义的运动是自然科学和社会科学面对的一致性要求。”[1]453-475理论和观察的互动得出结论：人类是构成自然的一部分，人类社会从自然界中分化出来后其运行的法则依然受自然规律的制约。难怪以前研究者提出疑问：“为什么人们的行为如同‘粒子’一样运动，行为是否遵从‘微观粒子’运行法则？”

追其史源，展望未来，科学发展路径正从分析走向综合，表征为科学理论趋于普适性和学科趋于交叉性：(1)就科学发展的老三论(控制论、信息论、系统论)及新三论(突变论、协同论和耗散结构论)而言，控制论创始人Wiener说：“无论是神经系统生命系统以至经济系统、社会系统，撇开各自的质态特点，都可以看作一个自动控制系统”[2]520；“信息论的创始人Shannon用信息熵对信息的度量以及经济中熵的引入在某种程度上是热力学熵的翻版[3]；Thom创立的突变论实质上等价于物理学中相变理论，用势函数描述股市的波动实际上是其在经济学中的应用；Haken协同学中的核心法则——奴役原理及其对变量的分类实质上类似物理学中的“绝热近似法”、经济学中长短期变量的区分；Tlya Prigogine创立的耗散结构理论已经广泛应用各个领域。(2)自然科学、社学科学在理论上的惊人相似，促使观察及深入研究的推进：Philip Ball从统计物理学视角研究社会，William Petty对政治算术的呼吁，Pierre Simon Laplace对巴黎人口性别用“误差曲线”的表征，哲学家Auguste Comte认为社会次序是自然法则的延伸。总之，正如Henry Thomas Buckle所说：“伟大的真理是人类的行为……在现实中并不矛盾，但是无论人类的行为表现得怎么反复无常，也仅仅是有序的宇宙系统的一个组成部分而已。”[4]133-140

在上述背景下，从宏观层次上的行星模型出发，根据普林斯顿大学John Q Stewart对大学科交叉的建议，“用类似物理的法则去研究社会经济系统，把社会法则转化为精密的数学法则”，结合德莱斯顿科技大学Dirk Helbing、德国Julich Forschungszentrum Gmbh研究所Armin Seyfried和佛蒙特州大学Taras I.Lakoba等人对社会作用力的定义“引入不同于自然科学中的行为改变的动力因子心理的因素”以及“要研究社会系统需建立抽象的距离空间”的建议，构建受激原子模型[5](古希腊模型、行星模型、量子模型)。基于上述趋势，立足前人研究的成果，从众多行为中分离出满足行为行星轨道等假设的部分行为，并从众多行为空间中抽象出禀赋空间，同时参照经典的力学体系建立形式类似万有引力公式的社会作用力模型(在某种程度上行为轨道更像粒子轨道，量子模型在模拟行为方面将更逼真；由于经济学缺乏相对严格的逻辑体系和基础变量的数理描述，所以只有先着眼于构建基础，逐层外推和逼近)，并测度其大小；然后对现实观测进行解释，而其正确程度依赖观察的深入和实践的推进。

假设条件：(1)在禀赋空间上行为轨迹为行星轨道；(2)行为的非随机性及其偏好的非饱和性；(3)行为的惯性定律[6]42-47。

一、行为行星轨道假设[注]行为的行星轨道状态是指一种既不完全不脱离群体行为、又不完全被群体行为同化的状态。下的行为间作用力模型建立

1. 问题分析

(1) 在禀赋空间中(禀赋空间可以看作一个行为空间)，任一携带行为惯量为ni的行子都处于其中的一位点，即行子执行一行为ri。而位点的改变都涉及对3种禀赋(经济Bx，道德By，权力Bz)的支索，故在任一时点上行子所执行的行为ri可记为

ri(t)=Bxi+Byj+Bzk

(1)

(2) 由假设(1)知，若一行为运动符合Kepler三大定律，即在禀赋空间中某一行为的改变在某种程度上可看作由决定行为的正反力量生成的均衡点的变化所引致的，则某一行子所执行的行为运动的轨道是椭圆的。①若行为惯性量为ni的行子i沿椭圆轨道围绕另一惯性量为nj的行子j运动，即i执行的行为受j执行的行为的吸引作用，并且j在i椭圆行为轨道上一个焦点上，在此i的行为轨道方程为

r=q/(1-ecosθ)

(2)

S′=r2ω/2=C

(3)

式中，ω=θ′，C为常数；③若行子i所处位点变化一周，即绕j一周运行的周期T的平方正比于椭圆长轴l的立方，则有[7]342-345

T2=Kl3

(4)

(3) 结合上述的推理，即行子i在禀赋空间中的运动轨迹为椭圆轨道，再由假设条件(3)及DirkHelbing对社会作用力的建议和定义可得

dωa/dt= fa(t)+fluctuationsdra/dt=va(t)=

(5)

再结合ArminSeyfried等人对上述模型的推广和改进，又由假设条件b可得[5]

fluctuations=0

(6)

成立。综上所述，在禀赋空间中社会力fi可以表述为

fi(t)=niai=ni(dvi/dt)

(7)

式中，vi(t)=dri/dt，ni是行子i的惯性量，即保持原行为状态的能力；ri是其在禀赋空间所处的位置，即行子所执行的行为；ai为行子在自发或者外界影响下执行行为的改变量。

2. 模型建立

在禀赋空间中，若t时行子i与行子j的距离记为r=r(t)，并构造一坐标系，使得其间行为位点的连线与x轴的夹角记为θ=θ(t)，即行子j执行的行为方向与x轴正向同向，则行子i的行为坐标就可表示为r=(rcosθ，rsinθ)，则由Kepler第二定律S′=r2ω/2=C，再根据Kepler第三定律及r2ω=2πlk/T，结合上述对社会力的定义fi(t)=niai以及Kepler第三定律T2=Kl3。综合推理，则j所执行的行为对i所执行的行为产生的引力可表述为

到了单位，高潮拿着最新一期的《NEW商圈》大样，到田卓办公室，请她签字。一进门，高潮就看到一位六十开外的老者坐在田卓的办公桌前，而田卓则站在他的身后，指着电脑屏幕，对他说着什么。见高潮进来，田卓忙向老者介绍高潮：这是我们《NEW商圈》的主编高潮。又向高潮介绍老者：我们德高望重的老领导马老。高潮赶忙趋前一步，向马老深鞠一躬。见马老抬起手来，高潮赶忙伸出手，和他握了一下。

fij(t)= [(4π2/nj)(l3/T2)][ninj/r2]rij=

(Hninj/r2)rij

(8)

式中，H=4π2K/nj为引力常量，rij=r(t)/r(t)=(cosθ，sinθ)，不妨设ni=1，则式(8)可整理为[7]

fij(t)=(Hnj/r2)rij

(9)

式中：H——两行子i与j所执行的行为间的吸引常数；

nj——被围绕具有较大惯性量的行子具有的惯性量，也可以看作处在某行业上的资本量，也可以理解为j执行行为的人数；

r——两行子在禀赋空间中所执行的行为之间的距离，即执行行为间的差距或者产业之间的距离；

rij——任一时点i行子的行为运动方向。

二、模型解释

如果把上述执行两种行为的行子看作两个群体i与j，通过一定的转化，则各群体执行行为的惯性量可以分别近似看作执行两种行为的人数。当把两个群体所执行的行为放在一个系统时，则两行为将发生交互作用，最终群体行为改变的量大小则由以下条件决定：

(1) 由式(4)得fi(t)=niai，由于fi(t)=fj(t)，则有下述成立：①若执行行为ri的群体具有的惯性量，即执行的人数大于群体j的人数，nj≤ni，则群体i行为改变的量将小于群体j行为的改变量，即|ai|≤|aj|成立，此时群体j所执行的行为取向更容易改变。②若群体i执行行为ri的人数小于群体j的，即nj≥ni成立，则群体i执行行为的改变量大于群体j的，即|ai|≥|aj|，故群体i所执行的行为更容易改变。

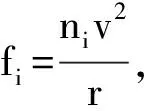
(4) 若在禀赋空间上任取一行为r1，并建立行业与行为，行为惯量和从事某种行业的资本之间的一一对应关系。执行此行为的所有个体可看作从事一行业的所有资本，若(x1，y1，z1)代表一行业，要使从事行业1的资本调出去从事行业3，即行子或者称为资本所从事的行业从r1转移到r3，则只需在r2方向上给予行业1上的资本一个f2的力，即可实现(如图2所示)。

图1 行为行星轨道

图2 禀赋空间

(5) 上述探讨社会作用力是在行为行星轨道假设下，即满足假设条件(3)的。脱离行星轨道的行为应具备什么样的行为条件呢?个体社会行为在禀赋空间的引力场中运行，其在坚持自己行为状态的同时也受来自空间内其他各种行为∑ri的影响，进而改变其初始行为r0的强度和方向，最终表征为新的行为迹线r(t)=r0+∑ri。 r(t)并不一定为椭圆曲线，而可能为螺线或者其他。为简化分析，单纯考虑二体系统(个体行为与群体行为构成的系统，同时忽视系统外的环境对其的作用)的相互作用力。个体行为所受力f(t)表征为外界其他个体对其的向心力f(in)和其坚持初始行为所致的离心力f(out)之和，在此有

f(t)=f(out)+f(in)

(10)

则对个体行为r(t)轨迹的操控，就归结为调节f(in)与f(out)的大小和方向。若使个体行为r(t)脱离行星轨道状态而向着被群体行为同化的趋势发展，则加大向心力|f(in)|；相反，若使得个体行为将来脱离椭圆轨道态并免受群体行为的影响，则改变离心力f(out)的方向，同时加大其强度|f(out)|。

三、结束语

为追求自然和社会在数学法则上的一致性，使得社会科学向精确化定量的轨道上切换，并把社会科学建立在自然科学之上，真正实现物理经济[8]的统一，本文构造制约社会经济研究向精确定量转化的禀赋空间，并在其基础上定义了类似自然系统的社会作用力，给出了行为之间的引力公式。同时，本文把矢量分析[9]引入对社会经济系统的研究中，进而弥补其在行为分析当中没有方向性的缺陷。利用上述理论，本文分析了社会经济系统内行为之间的相互作用以及集体行为[10]对个体行为的影响，并对个体行为的驱众给予一定的解释：“在所考察的系统内，因相对于集体行为惯性量个体行为的比较小，故行为易受群体行为的影响，行为改变量比较大”。同时，本文也对个体行为逃逸出集体行为的条件加以说明，这种方法不仅不是社会行为，同时对经济行为(如资本在各产业间的流动)有一定的解释力，即行为的空间可以延拓到产业空间，行为的惯性量可以推广到资本量。根据上面的论述，只要知道行为的惯性量，并能构造出满足条件的禀赋空间，就可以定量地测度行为之间的引力，并为调控行为施加一个恰当的力，而其正确程度则依赖观察的深入和实践的推进。

参考文献：

[1]陈平.文明分岔、经济混沌和演化经济动力学 [M].北京：北京大学出版社，2006.

[2]维纳.控制论 [M].北京：北京大学出版社，2010.

[3]王华，王云刚.基于信息熵的工程项目风险决策 [J].沈阳工业大学学报：社会科学版，2011(2)：154-158.

[4]牛文元.社会物理学国际前沿研究透视 [M].北京：科学出版社，2007.

[5]Henry T B.History of civilization in England(1857—1861)[M].UK：Media Corporation,2001.

[6]Art Hobson.物理学的概念和文化素养 [M].秦克诚,译.北京：高等教育出版社，2008.

[7]陈纪修.数学分析 [M].2版.北京：高等教育出版社，2004.

[8]黄昀，王胜.一门新兴的交叉学科：经济物理 [J].物理通报，2005(6)：9-12.

[9]张登兵，刘思峰.基于学习的互利协调与互制均衡及其矢量分析 [J].数学的实践与认识，2010(3)：64-69.

[10]徐浩庆.经济学和心理学中的羊群行为述评 [J].沈阳工业大学学报：社会科学版，2009(2)：132-138.