二进制域滑动窗口快速模乘算法

蒋洪波

(黑龙江科技学院 电气与信息工程学院，哈尔滨 150027)

二进制域滑动窗口快速模乘算法

蒋洪波

(黑龙江科技学院 电气与信息工程学院，哈尔滨 150027)

加速GF(2m)上的模乘运算是提高GF(2m)上ECC算法性能的关键。分析了窗口宽度ω的comb多项式乘法和NIST约简多项式算法，结合两种算法提出一种滑动窗口的快速模乘算法。该算法弥补了先乘后模方法在时间上和存储空间上的缺点，缩短了运算时间，仿真结果表明快速模算法的运算效率比先乘后模的窗口comb多项式乘法和NIST快速约简速度提高21%左右，预计算只需要ω-1个值。

滑动窗口;二进制域;快速模乘

0 引言

1976年Diffie和Hellman提出了一种公开密钥密码加密解密的新方法。基于椭圆曲线点群上离散对数问题(ECDLP)的难解性，椭圆曲线密码体制具有高度安全性，在同等安全强度下，其计算量小，存储量少，带宽小，软件和硬件实现的规模小，加密和签字速度高［1］。因此，ECC体制特别适用于计算能力、集成电路空间、带宽受限又要求高速实现的情况，如智能卡和无线通信等领域。

密码学中所使用的椭圆曲线最常见的有两类:质数曲线和二元曲线。二元曲线上的基本运算通常叫做二进制域上的运算。二进制域GF(2m)(下文以域代替)上基本运算简单和快速，其模乘算法主要有移位加模2和Montgomery算法［2］。目前最快的乘法算法之一是窗口宽度ω的comb多项式乘法。模乘结果必须在得到乘法结果之后再对其求模，这样会耗费很多运行时间，同时也需要存储2ω-1个预计算值。笔者提出的算法是在目前二进制域上从左向右窗口宽度ω的comb多项式乘法和NIST快速约简算法基础上，将两种算法相结合，实现减少循环次数同时也节省存储单元的目的。

1 comb多项式模乘算法

假设实现平台是字长W位的系统，其中W是8的整数倍。一个字U的W位，分别从0到W-1进行标记，其中第0位为最高有效位。

设f(z)是一个m次的二进制既约多项式，记f(z)=zm+r(z)，其中r(z)是一个次数最多为m-1的二进制多项式，则域的元素是次数最多为m-1的二进制多项式。域元素的加法就是二进制多项式的加法，域元素的乘法就是二进制多项式相乘并取模f(z)。

算法采用下列符号:C=(C［n］，C［n-1］，…，C［2］，C［1］，C［0］)是一个数组，则C{j}表示截短数组(C［n］，…，C［j+1］，C［j］)。

comb多项式模乘计算先进行comb多项式乘法，然后将结果作为求模运算的输入来求模。

1.1 窗口宽度ω的comb多项式乘算法

comb算法是López和Dahab在文献［2］中提出的。对所有次数低于ω的多项式u(z)，先计算出u(z)和域元素b(z)的乘积，并存储乘积。若ω=4则要有15个存储单元来存放预计算值。处理时查表一次计算出A［j］(t个ω字的一个数组)的ω位，其中a的位处理方向如图1所示。图1中的参数是m=163，W=32，ω=4。

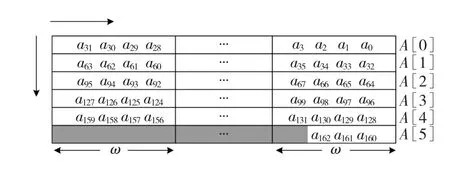
图1 窗口宽度ω的comb多项式乘法处理过程Fig.1 Process of polynomial multiplication about windows of width ω comb method

算法1 从左向右窗口宽度ω的comb多项式乘法

输入:次数低于m的二进制多项式a(z)、b(z)。

输出:二进制多项式乘积c(z)=a(z)·b(z)。

(1)计算Bu=u(z)·b(z)，对于所有次数低于ω的多项式u(z)。

(2)数组C清零。

(3)对于k从(W/ω)-1到0，重复执行。

①对于j从0到t-1，重复执行，

令u=(uω-1，…，u1，u0)，其中ui是A［j］的第(ωk+i)位，Bu+C{j}。

②若k≠0，则C←C·zω。

(4)返回(C)。

1.2 NIST快速约减算法

NIST约减多项式是NIST在文献［3］中推荐的快速模约减方法，字W=32，c(z)的次数最多为2m-2。

采用一次处理一个字的方法，例如，设m=163，W=32(共有6个字)，考虑c(z)模f(z)=z163+z7+ z6+z3+1的字 C［9］的约减，将字 C［9］表示多项式:

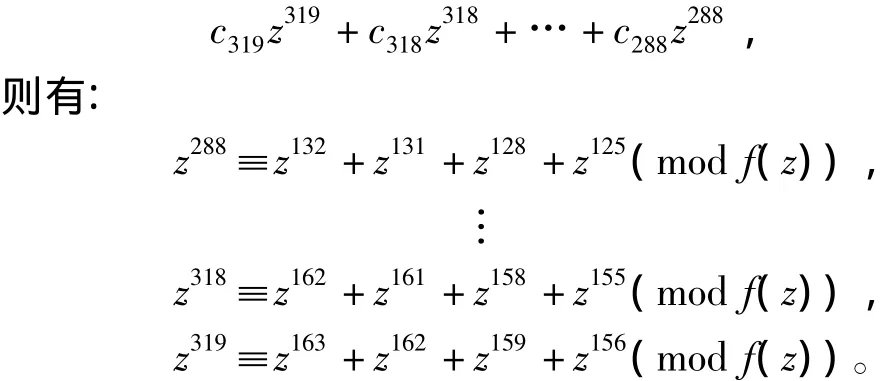
考虑上述同余式右边的四列，C［9］的约减可以通过把C［9］四次加到C上来实现(图2)，而C［9］的最高位四次分别加到C的132、131、128和125位上。同理，计算233位和283位求模运算［3］。

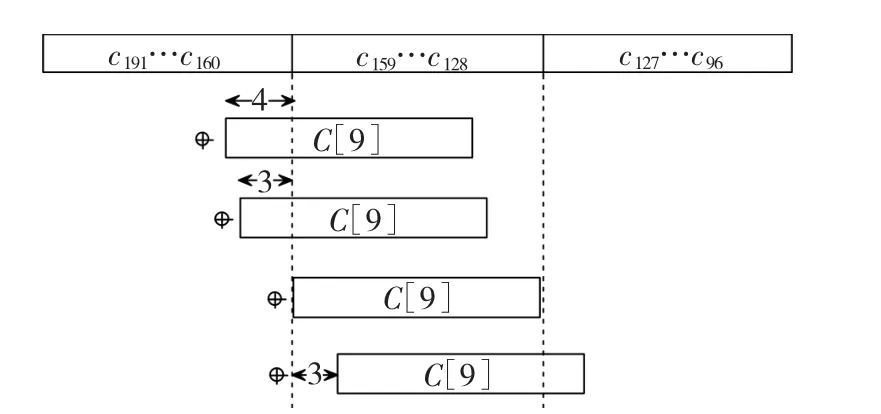
图2 约减32位字C［9］模f(z)=z163+z7+z6+z3+1Fig.2 Reducing 32-bit word C［9］modulo f(z)=z163+z7+ z6+z3+1

算法2 模f(z)=z163+z7+z6+z3+1的快速约减

输入:次数最高位324的二进制多项式c(z)。

输出:c(z)mod f(z)。

2 滑动窗口的模乘算法

对于∀a，b∈GF(2m)，a和b为次数低于m的不可约多项式，采用一次处理a的ω位的窗口方法［4-5］。算法需要进行预计算并存储其值，预计算的值有B21、B22、…、B2ω-1，共ω-1个值。宽度为ω的窗口从左向右进行滑动。ω=4时的滑动窗口如图3所示。

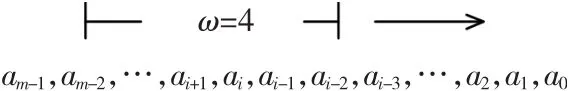
图3 ω=4时的滑动窗口Fig.3 Schematic diagram of sliding window for ω=4

图3中当前窗口中的数值为ai+1、ai、ai-1、ai-2，下一窗口的值为ai-3、ai-4、ai-5、ai-6。以此类推，直到最后的a3、a2、a1、a0。

NIST约减运算，先左移ω=4位后得到约减的值，只需运行算法2中的2～5步［6］。

由GF(2m)上的二进制减法和加法相同，故式(2)中的“-”可以用“+”代替，整理得

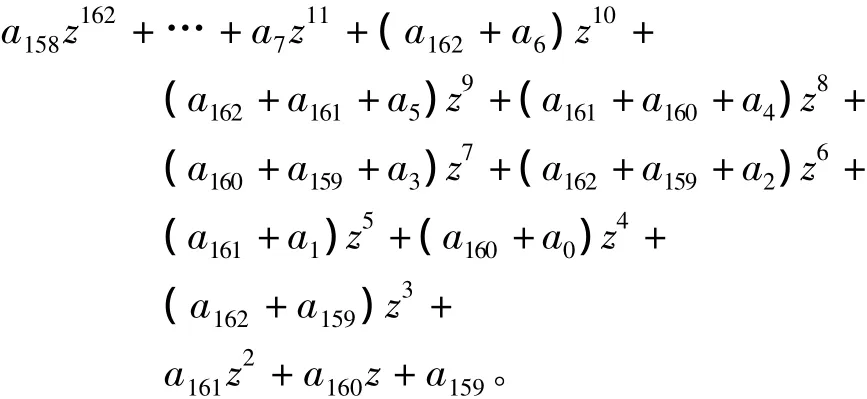
经上述分析提出算法3。

算法3 计算模乘的滑动窗口方法

输入:次数低于m的二进制多项式a(z)、b(z)。

输出:模乘结果c(z)=a(z)·b(z)mod f(z)。

(1)用文献［3］中的快速约减算法的第2～5步计算B21、B22、…、B2ω-1。

(2)数组c清零。

(3)对于k从0到(W/ω)-1，重复执行。

对于j从t-1到0，重复执行

①用文献［3］中的快速约减算法的第2～5步将c左移ω位，得到次数低于m的二进制多项式。

②令u=(uω-1，…，u1，u0)，其中ui是A［k］的(4j+i)位，利用已知的 B21、B22、…、B2ω-1计算Bu。

③c=Bu+c。

(3)返回c。

3 结果与分析

把算法1和文献［3］中的快速约减算法并用的求模乘的方法称作方法1，把模乘的滑动窗口方法称作方法2。方法1和方法2都是移位和异或操作。用来衡量时间效率的因素就只有循环次数了。在方法1和方法2中若取ω=4，则方法1的循环次数为［(W/ω)+1］·t+算法2中的循环次数+1(算法2中的循环次数根据m的不同而不同)，方法2的循环次数为(W/ω)·t。从算法的循环次数看，方法2要比先乘后模的方法1少些。

从预计算的值来看，若ω=4，方法1中的预计算是15个，方法2预计算3个值。方法2比方法1的预计算要少12个，这样更便于应用在存储受限的设备上。

对于方法1和方法2用C建模在Unix平台下，用gcc结果与分析编译得到的实验结果如表1所示。

从实验结果可以看到运算效率平均提高了21.06%。

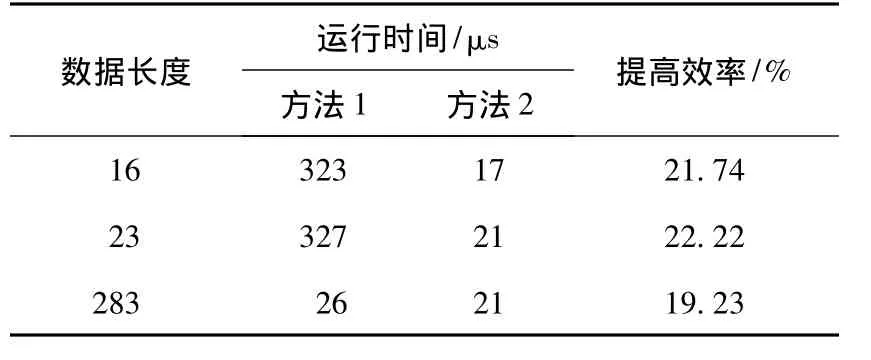
表1 ω=4时方法1和方法2算法运行时间Table 1 Running time of method 1＆method 2 for ω=4

4 结束语

笔者对文献［2］和文献［3］提出的乘法和求模运算进行了分析，在此基础上提出了一种基于滑动窗口的模乘运算。理论分析和实验证明，该算法只需要ω-1个预计算，计算效率比文献［2］和文献［3］结合使用方法的要高21%左右，在存储单元数量和计算时间上都有很大的改进。

［1］NEAL KOBLITZ.Elliptic curve cryptosystems［J］.Mathematics of Computation，1987，48:203-209.

［2］JULIO LOPEZ，RICARDO DAHAB，RICARDO DAHAB.Highspeed software multiplication in［C］.Progress in Cryptology—INDOCRYPT2000，2000:203-212.

［3］National Institute of Standards and Technology.Digital Signature Standard［S］.Washington:Federal Information Processing Standards Publication，2000:186-198.

［4］DARREL HANKERSON，ALFRED MENEZES，SCOTT VANSTONE.Guide to Elliptic Curve Cryptography［M］.New York: Springer-verlag，2004.

［5］李 忠，王 毅，彭代渊.基于滑动窗口技术的有限域GF (2n)乘法算法［J］.通信学报，2008，29(7):123-129.

［6］HAN YONGXIANG，BAI GUOQIANG CHEN HONGYI.Efficient VLSI Design and Implementation of an ECC Coprocessor over Binary Field［C］//何大可，黄月江.密码学进展:中国密码学会2007年会论文集.成都:西南交通大学出版社，2007:278-287.

Fast modular multiplication of sliding window based on binary domain

JIANG Hongbo
(College of Electric＆Information Engineering，Heilongjiang Institute of Science＆Technology，Harbin 150027，China)

Speeding up the modular multiplication holds the key to improving the performances of ECC algorithms in GF(2m).This paper presents an analysis of the comb polynomial multiplication(windows of width ω)and NIST reduction polynomials and features a faster modular multiplication algorithm of sliding window by combining the two operations.The algorithm can reduce the computing time by overcoming the shortcomings of modular-after-multiplication in time and storage space.The analysis of mathematic modeling and simulating shows that the new algorithms features computation efficiency about 21 percent greater than former modular-after-multiplication and NIST reduction polynomials and only ω-1 values are needed in pre-computation.

sliding window;binary field;fast modular multiplication

TN918.4

A

1671-0118(2011)05-0414-04

2011-06-16

蒋洪波(1978-)，女，黑龙江省鸡西人，讲师，硕士，研究方向:SoC、椭圆曲线加密，E-mail:88574099@163.com。

(编辑李德根)