基于相关系数优化法的河流突发污染源项识别
陈媛华,王 鹏,姜继平,郭 亮 (哈尔滨工业大学市政环境工程学院,黑龙江 哈尔滨 150090)
基于相关系数优化法的河流突发污染源项识别
陈媛华,王 鹏*,姜继平,郭 亮 (哈尔滨工业大学市政环境工程学院,黑龙江 哈尔滨 150090)
基于相关系数优化法,结合地表水环境特征和污染物水质过程特征,推导出一维河道中单点源瞬时排放的源项反演算法,得到了污染源排放特征与河流环境特征参数的反演公式.采用假想算例进行数值试验,综合分析了流速信息、污染物衰减、监测距离、监测数据误差及中间参数∆T选取等因素对反演结果的影响,确定了该方法的适用条件和最优条件的寻找方式.间隔10min进行两次监测采样,若监测误差小于5%,反演结果的相关系数达到-0.97,污染源位置和排放量反演结果的相对误差均小于4%,综合相对误差在2%以内.并且方法具有监测布点简单高效,数据需求低,编程简单等优点,值得在环境应急管理中进行实际应用.
点源污染源;河流突发污染;源项反演;参数识别;相关系数优化
世界各地都受到化学品泄漏事故的危害[1],其中地表水环境污染所占比重及对社会影响和损失最为显著.一些突发性水污染事故很有可能在事故初期不知道污染源的位置以及排放特征,甚至有些污染事故在污染团流出管辖范围后管理者才知道污染的发生,这对流域水环境管理十分不利. 因此需要找到有效的手段减少事故危害.上述问题可以描述为,已知污染物时空分布求解模型参数、结构和边界条件等信息,在数学上可以归纳为反问题[2-5].反问题广泛存在于环境水力学的各个研究领域,如废水排放污染源控制问题,水环境容量计算问题,污染物总量控制及分配问题等[6-8].
目前,地表水污染源反演研究越来越受到关注.如 Boano等[9]应用地学统计的方法识别河流中的污染源,张玉超等[10]采用支持向量机方法反演太湖叶绿素a的浓度分布,Cheng等[11]使用反向位置概率密度函数法和CCHE2D模型程序对河流污染源进行了识别,朱嵩等[12-13]采用贝叶斯方法进行了污染源识别和模型参数反演研究,牟行洋[14]利用微分进化算法研究了污染物源项识别反问题.
相关系数优化算法在地下水污染源识别问题研究中曾有应用[15],但地下水系统与地表水存在较大差异,此算法用于识别河流污染源的可行性有待研究.2007年郭建青等[16]尝试将其引入地表水参数识别体系,但尚未考虑污染物质在水体中的迁移转化规律(水质过程),并且算例的浓度数据直接来源于解析解的计算结果.因此极大地限制了算法的有效性和普适性.本研究在此基础上,结合河流的环境特征和污染物水质过程,考虑水力-水质耦合过程改进算法,得到了适用于可降解污染物的一维概化的地表水污染源识别方法.此算法可以反演出污染源特征(污染物排放量、污染源位置及初始排放时刻),同时计算出扩散系数和水流速,并考察浓度监测数据存在误差条件下算法的准确性和有效性.但本算法只适用于稳态流动条件下地表水污染物的迁移转化过程.
1 相关系数优化反演算法及修正
一维均一地表水瞬时点源排放流场的解析解[17]在许多教科书中可以找到:

式中:C(x,t)为瞬时脉冲排污引起的污染物浓度在水体的时空分布,mg/L;M为瞬时投放的污染物质量,kg;A为河流断面积,m2;Dx为纵向弥散系数,m2/min; k为污染物一级反应动力学衰减速率系数,min-1; u为河流平均速度, m/min; x0为污染源位置,m;t0为污染源排放初始时刻,min.
同一时刻监测水体中不同断面 xi污染物的浓度Ci,为简化计算将首次监测时刻设定为0时刻(t=0),污染物初始排放时刻先于监测时刻,故为负值.根据已知的一系列浓度数据求得5个参数, M、Dx、u、x0和t0(假定水的浓度ρ为1).
基于上述概化的水质模型和解析解,对以监测点与污染源位置的距离为自变量,污染物浓度对数值为变量的线性函数的相关系数取极值.求得污染源位置,然后选用另一组监测数据,求得其他参数.具体过程如下:
首先,对式(1)取对数,结果如下:
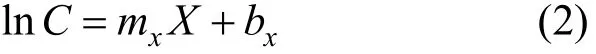
其中:

根据式(2)在直角坐标系中绘制浓度对数值关于(x–xm)2的曲线,可得到一条以mx为斜率、以bx为截距的直线.但由于污染源位置xm未知,无法确定横轴上各点的坐标, 因此尚不能确定此方程的斜率与截距.
对于任意的 xm值,可对式(2)进行线性回归,并且计算回归的相关系数.目标就是选取一个适当的xm值使相关系数达到最小,即最接近-1.式(2)的相关系数定义为:
n

式中:nx为监测点数;为平均距离,其表达式为:
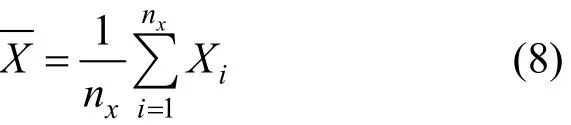
关于xm对相关系数最小化:

求导,可得:

其中,

可见,根据式(10)~(15)可以直接估算出污染源的位置(xm).实现了污染源识别的第一步.
确定xm后,通过式(4)可以计算得到Xi,然后,可对式(2)进行最小二乘法线性拟合.
可得,

从式(10)、式(16) 和式(17)可得xm,mx和bx.通过更进一步的检验发现只有 2个可以独立的用于求解的未知参数.因此,其余参数需要通过附加的条件确定.由于未知参数不能通过同一时刻的污染物浓度数据确定,其与监测点数目及浓度的时空分布无关.这些信息一定通过不同时间监测的污染物浓度提供.
为得到污染源的信息,需要估算全部的未知参数.首先,在取样的时刻(t=0)改写式(1):
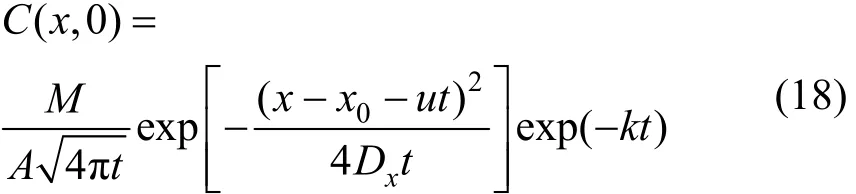
根据式(18)可以计算得到3个不同组合的参数:M,Dxt0和x0-ut0,其估计取值如下:
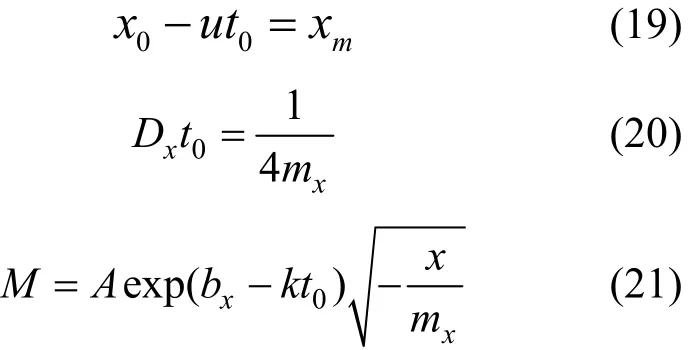
然后为了独立地求解出各个参数,污染物浓度数据必须取自一定时间后(∆t),同样按照式(10)和式(16)求得xm′和mx′,它们的定义是:


最后,根据上式能够计算出其余4个参数:

此外,根据式(21)可以计算 M,得到这些参数后,就可以实现反演计算过程.算法实际应用过程见图1.

图1 算法实际应用过程Fig.1 Process of applying the inversion algorithm
2 案例应用及反演计算影响因素分析
2.1 算例应用
2.1.1 算例来源 某点源污染源非常规瞬时排放进河流中一定数量的化学物质 α.事发一段时间后,预警系统进行响应,沿水流方向设置一系列监测点反演其排放历史,其位置见表 1.将解析解(式1)计算得到的结果Ci作为相应断面浓度数据的期望,加入高斯分布的白噪声[11],此处为5%.详细“观测”数据见表1.其他参数如下: M=3000kg; u=18m/min;Dx=60m2/min;k=0.001min-1;t0=-85min (第一次取样前 85min);x0=-1000m; A=20m2.为确定所有参数,在10min后进行第二次采样.
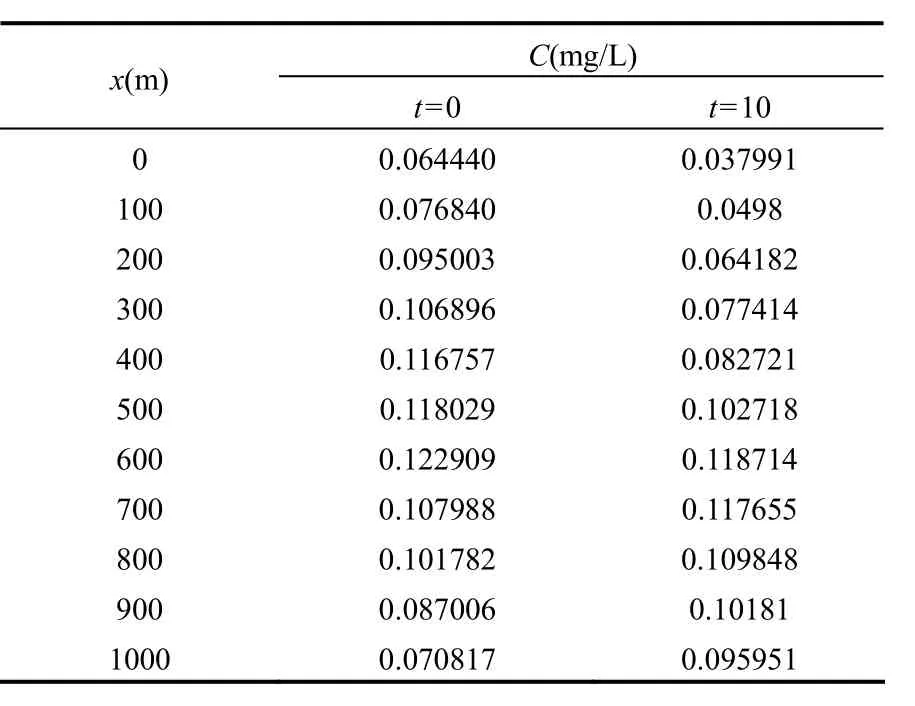
表1 瞬时点源算例的“观测”数据Table 1 Observed concentration data for the instantaneous source case

表2 算例污染源与参数反演结果Table 2 Estimated and real parameters for the conservative and decay instantaneous source case
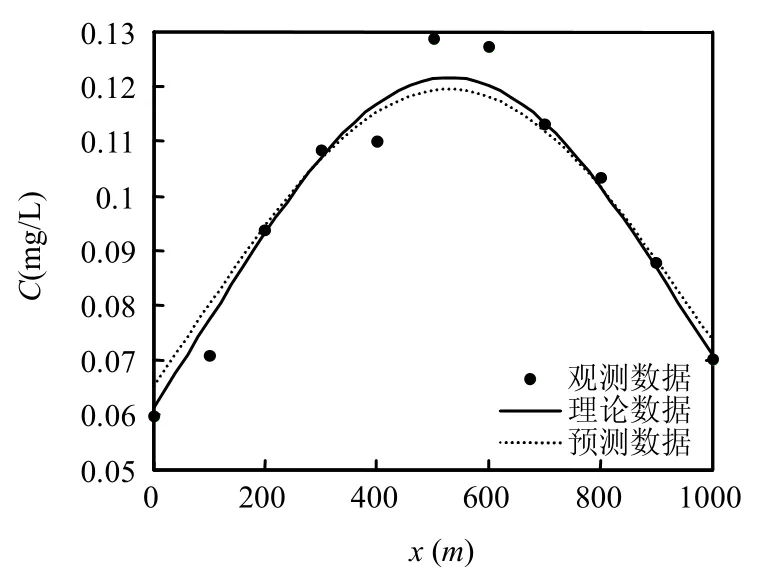
图2 t=0时刻瞬时排放点源的预测浓度数据和“观测”浓度数据Fig.2 Predicted and observed concentration for a conservative and a decay solute at t=0
2.1.2 反演结果 基于修正的相关系数优化法的反演计算公式,估算出未知参数见表 2.同时表2列出了将上述算例在不考虑污染物降解条件下进行反演的计算结果.估计参数与真实值接近,反演效果十分理想.图1为第一次采样时刻(t=0),实测数据、反演数据与理论数据的曲线.
由表2和图2可见,计算结果较接近假想算例中的真实值,相关系数绝对值达到了0.9747.
2.2 反演计算影响因素分析
2.2.1 河流流速的影响 实际研究中,河流的流速可方便获得.因此,考察水流速度条件已知与否对反演结果的影响.
由表3可知,速度条件对相关系数R没有影响.但其他参数的计算结果有所差别.本算例中流速已知的反演结果比未知时略差.

表3 流速对瞬时点源算例计算结果的影响Table 3 The impact of known velocity and unknown velocity for the instantaneous source case
2.2.2 污染物降解过程的影响 BOD是反映水体中污染物浓度的综合指标之一,其在河流中的降解系数一般为 0.039~20d-1[18].参照 BOD的降解系数范围,考察污染物在河流中迁移转化过程对反演结果的影响,因此选取化学物质 α的降解系数为0.001min-1,即1.44d-1.由图3可见,对于可降解的污染物质(k=0.001min-1),其在水体中的总质量随距离的增大而减少,因而在同一时刻同一位置其浓度小于非降解污染物;对于保守物质(k=0),则浓度计算结果偏高.但从反演结果(表2)可以看出,两者的计算误差均在5%之内,其中保守物质的计算结果较优于非保守物质,而考虑可降解物质的算法更适合应用于实际情况.
2.2.3 采样位置和时间的影响 构建一个评价指标,式(28)用向量的方法计算相对误差,用于考察采样位置和时间同污染源间的时空距离对算例中反演结果的综合影响.相对误差式中:为反演求得的参数向量;I为向量第i个参数;为真实值的参数向量.
由图4可见,在反演过程中,监测位置与时间是一对耦合的参数,共同影响反演结果.在二维的时空坐标下,源排放后 65~85min内在距污染源800~1000m的范围内进行第一次采样, 反演效果较好.

图4 监测位置和时间对反演结果的综合影响Fig.4 The impact of monitoring location and time on the inversion results
2.2.4 监测数据误差及两次采样时间间隔对反演结果的影响 利用相对误差考察采样噪声和时间间隔(∆t)对算例中反演计算结果的综合影响.
由图5可见,当采样的浓度噪声不超过5%,取样时间间隔对反演结果的影响较小;当浓度误差超过 5%时,随着误差增大,计算结果与真实值间的偏差越大.

图5 采样噪声和时间间隔对反演结果的综合影响Fig.5 The comprehensive impact of sampling noises and interval on the inversion results
3 结语
污染物在实际河流的迁移转化规律十分复杂,这对水质预测带了很大的困难.本文考虑了污染物水质特征,给出适于可降解污染物质的修正的相关系数优化反演算法,使本身运用于地下水的方法向地表水的特定环境下开展实际运用推进了一大步.本方法更适合实际情景的应用.
假想算例计算表明,本方法的计算结果接近真实情况,并探讨和分析论证其在实际运用时可能遇到的问题,具有一定的应用价值.
[1] 杨 洁,毕 军,张海燕,等.中国环境污染事故发生与经济发展的动态关系 [J]. 中国环境科学, 2010,30(4):571-576.
[2] 刘家琦.数学物理中的反问题及其数值解法 [J]. 科学探索1983,(3):75-83.
[3] 王彦飞.反演问题的计算方法及其应用 [M]. 北京:高等教育出版社, 2005:3-13.
[4] 刘晓东,姚 琪,薛红琴.环境水力学反问题研究进展 [J]. 水科学进展, 2009,20(6):885-893.
[5] Atmadja J, Bagtzoglou. A C. State of the art report on mathematical method for groundwater pollution source identification [J]. Environmental Forensics, 2001,(2):205-214.
[6] 闵 涛,周孝德.污染物一维非恒定扩散逆过程反问题的数值求解 [J]. 西安理工大学学报, 2003,19(1):1-5.
[7] Kitanidis P K, Vomvoris E G. A geostatistical approach to inverse modeling in ground water modeling and one-dimensional simulations [J]. Water Resource Research, 1983,19(3):677-690.
[8] 姜继平.水污染危险区域判定及其原型系统开发 [D]. 哈尔滨:哈尔滨工业大学, 2008.
[9] Boano F, Revelli R, Ridolfi L. Source identification in river pollution problems: A geostatistical approach [J]. Water Resource Research, 2005,41(7):W07023.doi:1029/2004WR003754.
[10] 张玉超,钱 新,钱 瑜,等.支持向量机在太湖叶绿素 a非线性反演中的应用 [J]. 中国环境科学, 2009,29(1):78-83.
[11] Cheng W P, Jia Y. Identification of contaminant point source in surface waters based on backward location probability density function method [J]. Advances in Water Resources, 2010,33(4): 397-410.
[12] 朱 嵩,刘国华,王立忠,等.水动力-水质耦合模型污染源识别的贝叶斯方法 [J]. 四川大学学报, 2009,41(5):30-35.
[13] 朱 嵩,刘国华,毛欣炜,等.基于贝叶斯推理的标准 k-ε湍流模型参数识别 [J]. 四川大学学报, 2010,42(4):78-82.
[14] 牟行洋.基于微分进化算法的污染物源项识别反问题研究 [J].水动力学研究与进展, 2011,26(1):24-30.
[15] Sidauruk P, Cheng A H D, Ouazar D. Groundwater contaminant source and transport parameter identification by correlation coefficient optimization [J]. Ground Water, 1998:36(2):208-214.
[16] 郭建青,李 彦,王洪胜,等.突然排污时计算河流水质参数的直线解析法 [J]. 水力发电学报, 2007,26(4):61-65.
[17] 郑 彤.环境系统数学模型 [M]. 北京:化学工业出版社, 2003: 43-46.
[18] 谢永明.环境水质模型概论 [M]. 北京:中国科学技术出版社,1996:124-130.
Contaminant point source identification of rivers chemical spills based on correlation coefficients optimization method.
CHEN Yuan-hua, WANG Peng*, JIANG Ji-ping, GUO Liang (School of Municipal and Environmental Engineering, Harbin Institute of Technology, Harbin 150090, China). China Environmental Science, 2011,31(11):1802~1807
A novel inversion algorithm based on an optimization approach for river point pollution sources was developed. Mass transport and kinetics processes of the contaminants in surface waters were combined along with the discharge history. And other relative parameters were deduced under the scenario that singular source instantly discharges degradable and soluble chemicals into one-dimensional rivers. A series of numerical experiments were carried out based on the hypothetic cases to analyze inversion effects associated with ambient river flow rates, contaminant decay rates, monitoring sites setting, sampling data errors and time intervals between two groups of sampling. When the monitoring time interval was less than 10 minutes and sampling data errors were controlled fewer than 5% approximately, the relative errors of pollution source location, total released mass and synthetical relative error are under 4%, 4% and 2%, respectively. Results show that parameters calculated fit well with the real values. In addition, the algorithms had the advantages such as efficient sampling process, minimum data requirement as well as easy programming. It was worthwhile to utilize this method for emergency environmental management practices.
point pollution source;river chemical spill;pollution source inversion;parameter identification;correlation coefficient optimization
X703.1
A
1000-6923(2011)11-1802-06
2011-02-01
国家自然科学基金资助项目(50821002)
* 责任作者, 教授, pwang73@hit.edu.cn
致谢:文章的英文部分由美国弗吉尼亚大学土木与环境工程系龙梧生教授修改与指导,在此表示感谢.
陈媛华(1986-),女,黑龙江哈尔滨人,哈尔滨工业大学市政环境工程学院硕士研究生,主要从事环境模拟与预警研究.发表论文1篇.

