含双参数的非线性二阶脉冲微分系统的正解
蔡静静
(同济大学 数学系,上海200092)
1 引言
本文研究下面二阶m点脉冲微分系统正解的存在性

其中λ>0,μ>0,ai>0,bi>0,ci>0,di>0,ai(t),bi(t)∈LP[J],1≤p<+∞,J=[0,1],ρi=aici+bici+aidi>0,ξj∈J′=(0,1),∈(0,+∞),i=1,2,j=1,2,…,m -2,fi,gi∈C(J×R+×R+,R+),Ii,k∈C(R+,R+).
微分系统(1)是含有脉冲项的多点边值问题,它能模拟许多物理现象,如描述由多个不同性质的部分组成的金属导线横截面的震动情况,而脉冲描述的是物体在某个时刻有突然变化.由于其广泛的背景,这类方程的研究受到广泛重视[1-4].最近,文献[1]利用不动点定理研究了下面的边值问题正解的存在性:

其中g(t)∈LP[0,1],f∈C([0,1]×R+,R+),笔者在条件 “f0=0,f∞=∞,或者f0=∞,f∞=0” 下得到问题(2)的正解.其中.然而不能解决当λ 变化及函数x 有跳跃时的情况.而本文是在参数λ及μ变化和函数x有多个跳跃点时利用不动点指数理论考察系统(1)正解的存在性.文献[2]得到了下面二阶m点边值问题的正解:

其中f连续.但实际问题中非线性项有时奇异甚至只是LP可积,此时文献[2]的方法不能解决这类问题.而本文研究的问题(1)中的非线性项有不同性质且其系数LP可积.
本文的主要思想来源于文献[1-2]等,并本质改进和推广了其中的结果,在非线性项有奇异性、函数含有脉冲点及参数可有不同取值范围情况下,不仅研究了正解存在性也讨论了正解不存在情况.
2 引理及一些结论
空 间PC1[0,1]:= {u∈C[0,1]:u′(t)在t≠ti处连续,且u′(t+i)和u′(t-i)存 在,u′(ti)=u′(t-i),i=1,2,…,n}在范数‖x‖=max{‖x‖∞,‖x′‖∞}下为Banach 空间.定义PC1[0,1]×PC1[0,1]中范数‖(x,y)‖2=‖x‖+‖y‖.本文作以下记号
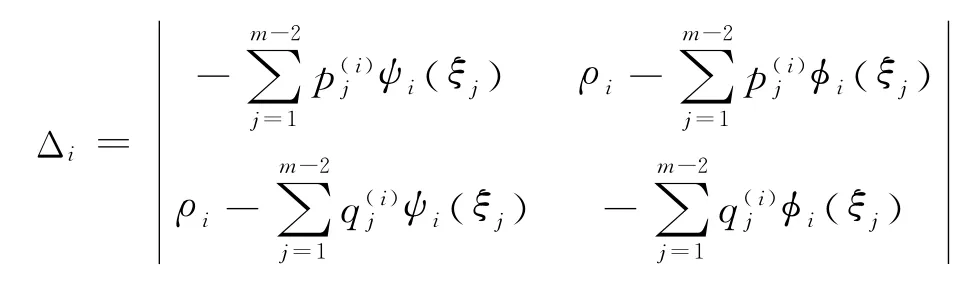
其中ψi(t)=bi+ait,φi(t)=ci+di-cit,t∈J是x″=0的线性无关解.对i=1,2,令

易知Gi(t,s)有以下性质:



本文对u,v∈R,i=1,2定义

其中μ=0或者μ=+∞.用g代替以上的f得到gi,μ和gμi的定义.记Fi(t,x,y)=ai(t)fi(t,x,y)+bi(t)gi(t,x,y)(i=1,2).记2×2矩阵的行列式,其中a,b为2维列向量.aT为a的转置.


引理1[5]设K是实Banach空间E中的锥,对r>0记.设A:全连续,且当时,则下面结论成立:

定义算子T:PC1[0,1]× PC1[0,1]→PC1[0,1]×PC1[0,1]如下:T(x,y)=(Aλ(x,y),Bμ(x,y)).则BVP(1)的正解等价于T的正的不动点.
引理2 设条件(A1),(A2)满足,则T:K×K→K×K是全连续的.
证明 由条件(A1),(A2)知,Aλ(x,y)(s)≥0,s∈J且 对于t∈Jθ有x(t)≥σ‖x‖,另一方面注意到对于t∈Jθ,s∈[0,1],有G(t,s)≥σG(s,s),ψ(t)≥σψ(s),故由Aλ(x,y),Bμ(x,y)的定义得Aλ(x,y)(t)≥σ‖Aλ(x,y)‖,Bμ(x,y)(t)≥σ‖Bμ(x,y)‖,从而T:K×K→K×K.同文献[2]可证明T全连续.
3 主要结果
定理1 假设(A1),(A2)和(H1),(H2)成立,则当μ和λ足够大时BVP(1)至少有两个正解.

证明 首先考虑当条件(A1),(A2),(H1),(H2)成立时.令



即

另一方面,由f1,∞=+∞知存在R1>1使得对于任意的及,有
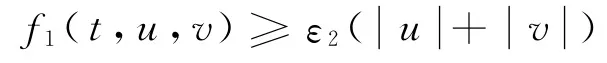


故

另一方面,由g2,0=+∞知存在R3>0且R3<1 使得对于任意的及,有


由式(6),(9),(11)及引理1知BVP(1)至少有两 个 正 解和并 且
注 满足(H1)和(H2)的函数gi很多,如gi≡常数;
定理2 设(A1),(A2)和(H3)成立,则当μ充分大λ充分小时BVP(1)至少有一个正解.

证明 由f1,∞=+∞知存在L1>0使得对任意的及有,令,则




其中ε0满足


因此由式(14),对于(x,y)∈∂Ω5有


故由式(15)和式(16),对于任意的(x,y)∈∂Ω5得到
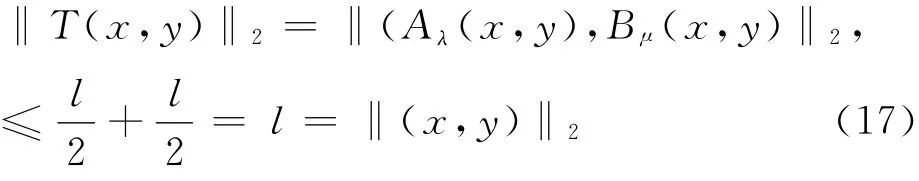
由引理1、式(12)和(17)知T有一个不动点
定理3 设(A1),(A2)和下面的(H*)成立,则当λ充分小时BVP (1)没有正解.
(H*)存在n(s)∈L[J,R+]使得
证明 假设BVP(1)存在正解(x,y),则x,y∈K,取,则有

这是矛盾的,因此BVP(1)没有正解.
[1] Zhang X,Feng M,Ge W.Multiple positive solutions for a class of m-point boundary value problems[J].Applied Mathematics Letters,2009,22(1):12.
[2] Feng M,Xie D.Multiple positive solutions of multi-point boundary value problem for second order impulsive differential equations[J].J Computational and Applied Mathematics,2009,223(1):438.
[3] Lomtatidze A.Positive solutions of boundary value problems for second order ordinary differential equations with singularities[J].J Differential Equations,1987,23(10):1146.
[4] Ren J,Ge W.Existence of two solutions of nonlinear m-point boundary-valve problems[J].Beijing Institute of Technology,2003,12:97.
[5] Guo D,Lakshmikantham V.Nonlinear problems in abstract cones[M].New York:Academic Press,1988.

