随机零矢量分配空间矢量PWM的谐波分析
吴志红,陈国强,朱 元,田光宇
(1.同济大学 汽车学院,上海201804;2.同济大学 中德学院,上海200092;3.清华大学 汽车安全与节能国家重点实验室,北京100084)
脉宽调制(pulse-width modulation,PWM)广泛应用于电能转换、调速、伺服等系统中,长期以来,是电力电子研究的主要内容之一[1-5].在基于数字信号处理器的电机控制中,广泛采用的是空间矢量脉宽调制(space vector PWM,SVPWM)技术,因为它具有直流母线电压利用率高、易于实现、谐波特性好等优点[6-7].由于实现简单,确定性调制方法(如固定调制周期、固定零矢量分配方式)被广泛采用,但是谐波主要集中在载波频率(调制频率)的整数倍附近,容易引起电磁辐射、声频噪声和机械振动等.虽然,提高调制频率可以得到改善,特别是若将调制频率提高到18kHz以上即可降低声频噪声,但是高的开关频率必然增加开关损耗[8].将集中于调制频率整数倍附近的集簇频谱展开进行平铺可以在较低的开关频率下减小开关噪声等不良效应.大量的文献对此进行了深入的研究,特别是随机PWM正在吸引着越来越多的学者为之努力.理论上,在满足 “伏-秒平衡”的约束下,所涉及的一切因素都可以注入随机特性,但是考虑到实现代价,只有部分方案具有实用价值.随机PWM可分为如下几类:(1)随机开关频率PWM[9-10]是原理最为明显,研究最多的一种方法,无论是在小调制比还是大调制比下都能获得良好的频谱展开效果.但是在闭环控制系统中,面临着电流采样、控制器参数确定等问题;(2)随机脉冲位置PWM是在满足基本矢量作用顺序和时间不变的情况下,通过改变三相控制信号高电平的位置,来达到展开频谱的目的[11].文献[8]对两相模式下随机对称中心PWM(随机脉冲位置PWM的一个特例)进行了研究,并提出了根据调制比的大小来选择零矢量进而进行随机化,可以在整个线性调制区获得良好的随机性能.随机脉冲位置PWM与随机开关频率PWM在一定的程度上是等价的[8].但是,同样面临着电流采样等问题.(3)随机零矢量分配PWM(random zero-vector distribution PWM,RZDPWM)是通过随机分配两个零矢量的作用时间来实现的[12-13].文献[1]对此进行了研究,并得出结论:在小调制比下,随机零矢量分配可获得良好的性能.(4)两种及两种以上随机方法的结合[14-15].在电机控制等闭环控制系统中,需要反馈相电流,同步采样得到的相电流更加接近于基波分量[16].固定周期的RZDPWM在电机的闭环控制系统中实现简单、方便电流同步采样,具有巨大的实用价值.谐波均方值和畸变率是评价调制策略的重要指标,很多文献对RZDPWM进行了卓有成效的研究,但是都没有给出RZDPWM谐波均方值和畸变率的计算公式.
PWM在一个调制周期内以 “伏-秒平衡”原理为基础,以多边形磁链逼近圆形磁链,必然导致逼近误差.再者,由于电力电子器件固有的开关特性,其电压控制总是伴随着谐波[7].基于此,本文通过综合分析磁链谐波、电流谐波,推导RZDPWM策略下磁链/电流的谐波均方值和畸变率的计算公式.
1 RZDPWM的基本原理
经典的两电平三相逆变器[6-7]共有8种开关状态,对应着8个基本电压矢量,其中包括6个非零电压矢 量(U1(100),U2(110),U3(010),U4(011),U5(001),U6(101))和两个零电压矢量(U0(000)和U7(111)).如图1所示,括号中的数字1表示上臂导通,0表示上臂不导通,每相的上下臂导通状态互补;αβ为两相静止坐标系;A,B,C 为三相标号.对于幅值为Uo、相角为θ的参考电压矢量Us可由临近的两个非零基本电压矢量和零矢量按照 “伏-秒平衡”的原则进行合成.图1 所示的是在第一区的情况,设Us,U1,U2作用的时间分别为Ts,2T1,2T2,则

图1 基本电压矢量及合成Fig.1 Basic voltage vectors and the reference vector generation method

零矢量U0和U7作用时间为2T00和2T07,总时间为

为了方便数字控制系统实现,广泛采用的两个零矢量作用时间均分的对称7 段式调制策略如式(3)所示,以下称此为SVPWM.

在RZDPWM中,两个零矢量作用时间随机分配,设半个PWM周期内U7的作用时间为

式中,ε为随机变量.
则U0的作用时间为

2 磁链谐波产生的原因
圆形磁链是通过多边形磁链来逼近,多边形的边数取决于载波比.随着PWM频率的提高,逼近误差越来越小.因此,在进行磁链谐波分析时,假定多边形边数为无穷,此时多边形磁链就变成了圆形磁链.这是磁链谐波分析的基本假设.
在忽略定子电阻时,参考电压矢量为磁链矢量对时间的导数,电压矢量与磁链轨迹相切.如图2所示,参考电压矢量是由临近的两个基本矢量和零矢量合成的,所以,实际的磁链轨迹在理想的轨迹附近波动,不断穿越理想轨迹.其法向误差带的形状如图3所示,误差带的宽度为

图2 磁链谐波示意图Fig.2 Diagram of the harmonic flux

图3 磁链误差带图Fig.3 Diagram of the flux error region

从式(6)和图3可以得出:(1)磁链法向误差带的宽度随着调制比的增大而增大.这是因为在相角相同的情况下,调制比的增大使得两个非零基本矢量的作用时间增加,由于参考电压矢量(相角为0°,60°,120°,180°,270°时除外)与合成的基本矢量相角并不相同,所以基本矢量在法向上的误差(图2中的h)会增大.(2)在每个区的边界(见图3),误差带最大,距离边界越远,误差越小;在区的中心法向误差为零,因为此时参考电压矢量与基本矢量的方向一致.(3)磁链切向误差对相角依赖不大,但是对调制比依赖较大.切向误差的最大值取决于零矢量的作用时间和分配方式,随着调制比的增大,零矢量作用时间减小,切向误差减小.
参考电压矢量是由临近的两个矢量和零矢量合成的,而这些基本矢量和参考矢量之间存在差值,可定义电压误差矢量

谐波是由切向误差和法向误差共同形成的,7段合成方法的误差三角形如图4所示[1,6].F为参考电压矢量Us的端点;H,I,J和L,K,P为两个三角形的顶点;D和E为两个三角形的质心;l为质心到Us的端点的距离.三角形的形状和大小与调制比、参考矢量的相角、零矢量分配方式都有关.在SVPWM中,两个三角形的边IJ和PK完全重合;在RZDPWM中,重合度是随机的.

图4 磁链和电压误差矢量图Fig.4 Trajectory of voltage and flux error vector
3 谐波均方值及畸变率公式的推导
在感性占主导地位的负载中,磁链矢量和电流矢量之间只相差一个大小为等效电感的比例因子,因此,磁链矢量误差三角形和电流矢量误差三角形是相似的.因此,本文只对电流谐波均方值和畸变率计算公式进行推导.文献[7]以三角形负载为例,给出了谐波电流均方值的表达式

式中:u1=eA/(UDC/2) ;u2=eB/(UDC/2) ;Lσ为 等 效电感;eA,eB为PWM周期内的平均电压.
谐波畸变率(harmonic distortion factor,HDF)为

3.1 SVPWM的微观(PWM周期)谐波畸变率
对于经常采用的SVPWM,ε=0.由于7段调制方法的对称性,因此只需要分析前半个PWM周期即可.6个区具有对称性,所以仅在第一区进行推导.三相电压在半个PWM周期内的平均值为
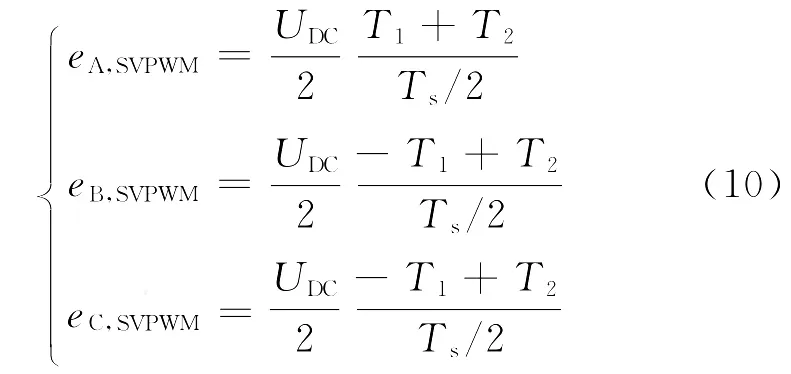
用式(10)替代式(8)和(9)中的平均电压,分别计算fAB(M,θ),fAC(M,θ),fBC(M,θ),三 者 相 加可得

3.2 SVPWM的宏观(基波周期)谐波畸变率
由文献[7]可得SVPWM的宏观HDF

3.3 RZDPWM的微观(PWM周期)谐波畸变率
在RZDPWM中,式(10)的平均电压多了一项
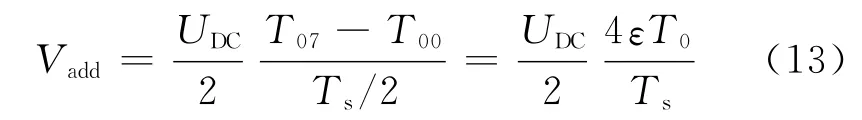
令

则

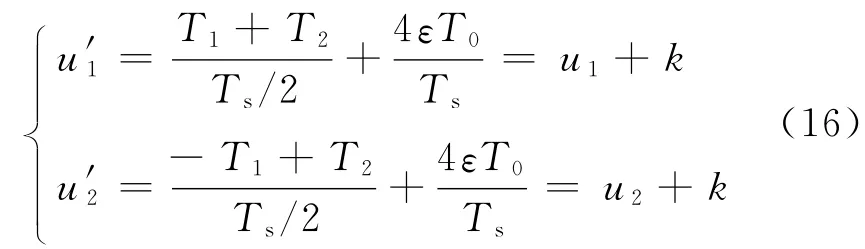
对式(8),考虑

那么只需要对多出来的一部分进行分析,令

由此可得NAB,同理可得NAC和NBC,如下

三者相加并将式(1),(2)代入,可得


因此,RZDPWM的微观HDF为

3.4 RZDPWM的宏观(基波周期)谐波均方值
考虑到对称性,只需要对ΔiAB在半个基波周期进行计算即可.在第一区中

因为ε为随机变量,可设数学期望

因为N1(ε)是个随机变量,对其数学期望E[N1(ε)]在(0,π/3)积分,可得

在第五区中

式中:T1,T2为基本矢量U5,U6的作用时间.
对E[N5(ε)]在(4π/3,5π/3)积分,可得

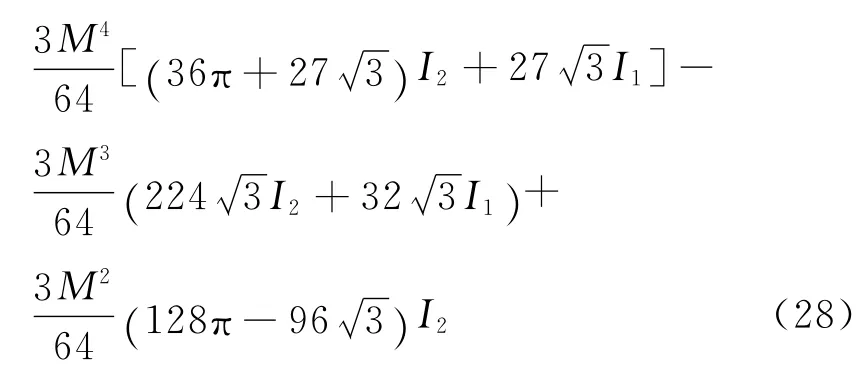
在第六区中

式中:T1,T2为基本矢量U1,U6的作用时间.
对E[N6(ε)]在(5π/3,2π)积分,可得

因此,RZDPWM的宏观HDF为

则在基波周期内,电流的谐波均方值为

4 结果讨论与仿真实验
根据本文推导的RZDPWM的HDF 公式(31)和文献[7]给出的经典的连续与不连续PWM(discontinuous PWM,DPWM)策略HDF 的表达式,可绘制图5.图中,SPWM为正弦脉宽调制,
DPWM0, DPWM1, DPWM2, DPWM3,DPWMMAX,DPWMMIN 为6 种不同的DPWM.因为不连续调制的开关次数比连续调制减少约1/3,因此其开关频率可以提高到以前的3/2倍,因此,图中将两种情况绘制在一起.从图5,可以发现如下规律:
(1)当调制比很小时,非零矢量作用时间短,零矢量作用时间虽然长;但是此时误差矢量e0长度很小,误差三角形小,极端的状况是调制比为零时,三角形缩为一个点.因此,此时谐波畸变小.总的来说,随着调制比的增大,误差三角形变大,则HDF增加.
(3)RZDPWM下,随机变量ε2的特征影响HDF,在图5 所绘制出的三种分布中,均匀分布时HDF最大,正态分布(3 倍标准差为0.5,只保留[-0.5,0.5]的部分)最小.这是由于在这三种分布中,正态分布时数学期望最小,均匀分布时最大.这在一定程度上也说明了SVPWM在零矢量分配上是准优的.

图5 不同调制策略下宏观HDFFig.5 HDF for the various modulation strategies
如果将误差三角形看作线密度均匀的框架,则谐波的均方值即为此三角形框架绕固定转轴(在复平面内的投影为参考电压矢量的端点,图4 中的F点)的转动惯量(之间相差一个比例因子,但不影响问题的分析).转动惯量的平行轴定理为:刚体对于任一轴的转动惯量等于刚体对于通过质心、并与该轴平行的轴的转动惯量,加上刚体的质量与两轴间距离平方的乘积.则谐波均方值λ2rms为

式中:J0为每个三角形绕着自己质心D,E 的转动惯量;m为每个三角形框架的质量;l为三角形质心D、E到参考电压矢量端点的距离.
在SVPWM中,两个零矢量作用时间是相等的,即IF=KF=PF=JF;在RZDPWM中,两个零矢量作用时间随机分配,也就是说,在保证参考电压矢量端点F固定、两个三角形在PJ直线上的边有重合的前提下两个三角形沿着直线JP随机朝相反的滑动.对于SVPWM和RZDPWM来说,式(33)右边的第一项2J0是相同的,不同的是式(33)右边的第二项2ml2.当调制比很大时,边JI和KP很小,两个三角形滑动的范围很小,l的变动范围很小.此时,RZDPWM与其他调制策略的谐波趋于一致.
在3.1和3.3部分分析微观HDF时,是将三相的电流的HDF相加;而在3.4部分推导宏观HDF时只包含了一相.实际上,如果将式(23)在区间(0,π/3)积分,并求均值,也可得到宏观的HDF,只不过得到的结果是三相的相加,则为单相时的3倍.为了便于和图5 比较,在绘制微观HDF 时将其缩小3倍.
如果PWM周期趋于0,则RZDPWM的微观HDF就变为瞬时值,均匀分布时在6 个区内HDF的数学期望如图6所示.图7给出了与SVPWM相比,RZDPWM(均匀分布)增加的HDF.

图6 RZDPWM在整个线性调制区的微观HDFFig.6 HDF for RZDPWMin the linear modulation zone

图7 RZDPWM比SVPWM增加的微观HDFFig.7 Increased HDF for RZDPWMrelative to SVPWM
从图7 可以看出,随着调制比的增加,RZDPWM增加的HDF先增大随后又减小.这与图5所示的宏观上HDF的变化趋势是一致的.
在计算机上对三相逆变器拖动电机进行仿真,基波频率为30 Hz,PWM频率为2.2kHz.仿真测得的定子电流的轨迹如图8所示,为了更加清楚地表现误差带的形状,在绘图的时候,将谐波幅值进行了放大.电流矢量误差带与图3所示的理论误差带形状基本一致,随着PWM频率的不断提高,误差带将越来越趋近图3所示的理论误差带.在SVPWM中,两个三角形沿着圆形轨迹匀速向前推进;但是在RZDPWM中,由于零矢量的随机分配,使得三角形前进的速度呈随机性.

图8 测得的电流矢量轨迹Fig.8 Measured current vector trajectories
5 结论
本文对RZDPWM的磁链/电流谐波进行了深入分析,并推导出了磁链/电流谐波均方值及畸变率在微观(PWM周期)和宏观(基波周期)上的理论表达式,最后对理论结果进行了讨论并用仿真实验进行了部分验证.得出了如下结论:
(1)磁链误差主要来源于多边形逼近误差和PWM“伏-秒平衡”原理带来的误差,随着PWM频率的不断提高,后者为主要因素;
(2)随机分布的特征对RZDPWM的谐波均方值及畸变率有较大影响,随机数的数学期望越大,谐波越大.当调制比接近最大值时,随机化效果变差.此时,常见的几种PWM谐波趋于一致.虽然RZDPWM的谐波比SVPWM有所增加,但是它的谐波集簇效应比SVPWM小;
(3)在SVPWM中,稳态时磁链/电流矢量误差三角形沿着理想的圆形轨迹匀速前进; 在RZDPWM中,误差三角形前进的速度呈随机性.也就是说,磁链/电流矢量轨迹的切向误差在随机变化.这种非周期性地前进是频谱展开的根本原因.
[1] Bech MM,Blaabjerg F,Pedersen J K.Random modulation techniques with fixed switching frequency for three-phase power converters [J].IEEE Transactions on Power Electronics,2000,15(4):753.
[2] 杨恩星,仇志凌,陈国柱,等.并联双PWM变流器在低速永磁直驱风力发电系统中的应用[J].电力系统自动化,2009,33(10):95.YANG Enxing,QIU Zhiling,CHEN Guozhu,et al.Application of parallel dual PWMconverter to the low-speed permanent magnet direct-driven wind turbine[J].Automation of Electric Power Systems,2009,33(10):95.
[3] 王立乔.正弦波逆变器脉宽调制技术的调制模型分析[J].电力系统自动化,2008,32(16):45.WANG Liqiao.Modulated model analysis of pulse width modulation technique for sinusoidal inverters[J].Automation of Electric Power Systems,2008,32(16):45.
[4] 张颖超,赵争鸣,鲁挺.基于RTW 的三电平双PWM变换器控制系统设计[J].电力自动化设备,2009,29(10):128.ZHANG Yingchao,ZHAO Zhengming,LU Ting.Control system for three-level dual-PWMconverter based on RTW[J].Electric Power Automation Equipment,2009,29(10):128.
[5] 袁登科,徐国卿,张舟云,等.一种新型空间电压矢量脉宽调制方[J].同济大学学报:自然科学版,2008,36(12):1702.YUAN Dengke,XU Guoqing,ZHANG Zhouyun,et al.Research on a novel space vector pulse width modulation method for voltage-source inverter[J].Journal of Tongji University:Natural Science,2008,36(12):1702.
[6] Hava A M. Carrier based PWM-VSI drives in the overmodulation region[D].Madison:Wisconsin University.College of Engineering,1998.
[7] Holmes D G,Lipo T A.电力电子变换器PWM技术原理与实践[M].周克亮译.北京:人民邮电出版社,2010.Holmes D G,Lipo T A.Pulse width modulation for power converters:principles and practice[M].Translated by ZHOU Keliang.Beijing:Posts & Telecom Press.2010.
[8] Oh S Y,Jung Y G,Yang S H,et al.Harmonic-spectrum spreading effects of two-phase random centered distribution PWM(DZRCD)scheme with dual zero vectors[J].IEEE Transactions on Industrial Electronics,2009,56(8):3013.
[9] 马丰民,吴正国,李玉梅.随机频率PWM逆变器的分析设计[J].中国电机工程学报,2008,25(14):67.MA Fengmin,WU Zhengguo,LI Yumei.Analysis and design of the random frequency PWMinverters [J].Proceedings of the CSEE,2008,25(14):67.
[10] 王颢雄,王斌.基于三状态马尔柯夫链的随机周期调制PWM技术研究[J].中国电机工程学报,2007,27(4):8.WANG Haoxiong,WANG Bin.Study of randomized period modulation based on three-states Markov chain [J].Proceedings of the CSEE,2007,27(4):8.
[11] Na S H,Jung Y G,Lim Y C.Reduction of audible switching noise in induction motor drives using random position space vector PWM[J].IEE Proc Electr Power Appl,2002,149(3):195.
[12] 马丰民,吴正国,李玉梅.随机零矢量分配RPWM的实现及其功率谱分析[J].武汉理工大学学报,2007,31(2):239.MA Fengmin,WU Zhengguo,LI Yumei.Realization and power spectrumanalysis of random zero-vector PWM[J].Journal of Wuhan University of Technology,2007,31(2):239.
[13] 马丰民,吴正国,侯新国.基于统一PWM调制器的随机空间矢量调制[J].中国电机工程学报,2007,27(7):98.MA Fengmin,WU Zhengguo,HOU Xinguo.Random space vector PWMbased on the generalized modulator [J].Proceedings of the CSEE,2007,27(7):98.
[14] 王庆义,邓歆,刘洋,等.一种零矢量-变延时随机PWM方法[J].电工技术学报,2009,24(12):132.WANG Qingyi,DENG Xin,LIU Yang,et al.Amethod of zero vector and variable delay randomized PWM[J].Transactions of China Electrotechnical Society,2009,24(12):132.
[15] 王斌,李兴源,王颢雄,等.基于马尔可夫链的双随机PWM技术研究[J].电工技术学报,2005,20(6):16.WANG Bin,LI Xingyuan,WANG Haoxiong,et al.Study of the dual randomized modulation based on Markov chains[J].Transactions of China Electrotechnical Society,2005,20(6):16.
[16] 耿华,于艾,杨耕.SVPWM逆变电源电流采样方法的比较[J].电力电子技术,2005,39(6):136.GENG Hua,YU Ai,YANG Geng.Comparison of methods for current sampling in SVPWMinverter[J].Power Electronics,2005,39(6):136.

