城市轨道交通线路客流分布的实时预测方法
徐瑞华,徐永实
(同济大学 交通运输工程学院,上海201804)
轨道交通线路客流分布实时预测是指对当前时段轨道交通客流在各区间断面、站台、列车上的分布状况进行实时计算,并对未来若干时段内的客流分布状况进行预测的过程.轨道交通客流实时预测的结果既可以提供给运营管理部门用作对轨道交通运营计划进行实时调整的依据,也可以提供给轨道交通乘客作为安排出行的参考,因而具有重要的应用价值.
要进行客流分布实时预测,首先需要获得当前时段及未来若干时段内进站客流的完整的OD 信息,这里提到的 “完整的OD 信息”是指:①当前时段乘客进站、出站的站点信息俱全;②当前时段乘客进站时刻信息具备,且需要精确到分钟或秒;③当前时段进站客流流量变化规律.当前轨道交通的自动检售票系统(automatic fare collection system,AFC),在任何时刻都只能获取乘客的进站信息,乘客的去向(即完整的OD 信息)要在乘客到达目的地以后才能获得,显然不能满足实时预测的要求.目前,已有的轨道交通客流分布算法是建立在假定已经获取了完整的OD 分布信息基础之上,例如文献[1-2]对如何获得完整OD 信息还需要深入分析.
其次,现有的各类轨道交通客流预测方法基本都是采用了静态分配方法[3-5],即将OD 按照路径阻抗函数值进行各路径客流分配,这种方法没有考虑到列车车辆处于动态运行之中,无法对车辆、乘客进行实时定位,因而无法准确计算线路上各站台、断面以及各班次列车上客流的实时分布状况.轨道交通客流在各线路站台、区间断面、列车上的分布是相互关联、相互影响的有机体,站台上候车乘客的特征决定着列车载客量,而列车载客量反作用于站台,表现为站台乘客等待时间的变化,线路各区间断面客流量的大小则由通过该断面的各班列车载客量所决定.因此,进行轨道交通客流实时预测需要完整地、系统地分析三者之间的相互关系,目前已有的算法尚不能满足要求,本文通过建立了站台一列车客流交互模型解决了这一问题.
1 城市轨道交通线路实时客流分布状态预测方法
1.1 实时客流分布状态
轨道交通线路客流分布是指客流在轨道交通线路区间、列车、站台上的分布状况,在对实时客流分布状态进行预测和分析中主要应得到的指标可以归纳为以下几个:
(1)实时断面流量:定义为线路上任一区间中某断面位置在某统计时段内通过的乘客数量.该参数在数量等于在该统计时段内通过的所有列车的载客量之和,是进行列车运行计划调整的重要指标.
(2)实时列车满载率:定义为任一时刻任一班次列车实际载客量与该列车定员数的比值.易知,任一列车在任一区间内的满载率等于该列车从该区间上游端点站台出发时的满载率,因而记作γjk,以表示该线路第j班列车从编号为k的站台发出时的满载率.该参数反映了车厢内的拥挤状况,是为乘客出行提供信息诱导的主要指标.
(3)站台平均等待时间定义为:任一时段内到达k站台的所有乘客的平均等待时间.站台平均等待时间反映了列车开行计划对站台乘客的疏导能力,也是为乘客出行提供信息诱导的主要指标.
1.2 实时客流分布状态预测的关键
根据目前轨道交通票务运营方式,无法实时检测进入站台乘客的去向,乘客的目的地要到达时才能检测到,即从乘客进入站台至获得乘客的完整OD信息在时间上相隔整个出行时间,完全不符合实时监测的要求,为此,本研究通过对大量的轨道交通运营历史数据进行分析后发现,全天乘客出行的站间OD呈现较大的规律性,因而可以将一年中具有相似分布规律的日子归为几类特征日,如工作日、双休日、特殊节假日等,然后在这些特征日中分别将全天OD 划分成若干时段,在这些时段内的OD 变化比较小,呈现一定的稳定性.划分的时段越大,误差越大,而划分的时段越精细,则个体差别性表露越明显,误差也越大,因此,需保证划分的各时段内有足够的样本数,以充分显示其统计规律,同时时段不应太大而失去了OD 的变化特征.本研究中采用各站台各班次列车发车间隔为统计OD 的时段可以保证上述要求的实现.对任一站点k,其OD 比例表记为表Bk,Bk|ji为该表中的第i行第j列数据值,含义为k站台,在时段[ti-1k,tik]内进入站台的乘客在站j下车的分配比例.
在轨道交通网络运营条件下计算各线路的实时客流分布状况时,首先需要将网络上所有的站间OD量分配到连接OD 的可能路径上,然后利用单条线路的实时算法对网络中各条线路的实时运行状态进行计算.因此需要对网络中所有OD 进行可行路径搜索,并在一定客流分配规则下确定各路径的分配比例,然后确定各线路各时段的站间OD 分配比例.文献[6]中提出了基于深度优先的路径搜索算法和路径客流分配比例计算方法,在此不再详述.
2 实时客流分布状态预测模型及算法
2.1 模型假设
(1)线路几何结构,包括:站点及编号(1,2,3,…,m);各相邻站点之间的距离.
(2)列车开行计划,包括:该线路全天开行的列车班次及发车间隔,实际情况中,全天的发车间隔不是固定的,有高峰间隔、平峰间隔、低峰间隔之分,本文的计算方法考虑了这一点,这也是本文与其他算法相比更符合实际之处.记tjk为第j班次列车离开k站台的时刻,则[tj-1k,tjk]表示两相邻班次列车从k站台发出的时间间隔,下文中除特别指出外的时间间隔都是指[tj-1k,tjk].
(3)各站台的乘客实时到达规律
站台乘客的实时到达规律可以通过对在站台入口合理设置计数器采集的数据分析处理得到,具体方法为:取一时间段为单位时间段,例如以5s为一个计时单位,将单位时间内到达的乘客近似处理为均匀到达,因此可以构建一个以k站台乘客到达率为变量的到达函数gk(t),由于gk(t)是任一确定时段上只有有限个第一类间断点的有界函数,因而gk(t)在任一确定时段上是可积的.
2.2 基于站台—列车客流交互的预测模型
由于各班次列车到达某站时的实际载客能力、站台候车乘客数量不同,所以各班列车的实际上客量也不同,使得寻找站台乘客上车规律增加了困难.但是,如果以站台对各班次列车的上车比例为联系参数,则能比较容易地发现其中的规律.
记列车j在k站台的上客比例φjk为实际上车乘客数与列车j停站期间k站台等待乘客数之比,此参数的具体数值计算可以在本文后面的算法中逐步计算得到.
对于任一时段[tj-1k,tjk]内到达k站台的乘客在任一列车j(j≥i)上的分配数量Ak|ji为

任一时段[ti-2k,tik]内到达k站台的乘客在任一列车j(j≥i)出发后剩余的乘客数为

运用数学归纳法很容易证明上述表达式成立,限于篇幅,证明过程从略.
从式(1)中可以得到以下结论:
(1)如果某班次列车i在该站台的上车比例为1,说明站台乘客全部被该列车i载走,站台没有滞留,即该站台在时刻tik之前进站的乘客在i列车到达时全部被载走,那么在时刻tik之前进站的乘客在i列车后面的各班列车j>i上的分配量为零.
(2)如果某班次列车j以前的所有班次列车在该站台的上车比例均不为1,说明时刻列车j以前的各班次列车从k站台发出时站台都有滞留,那么在时刻tjk之前进站的乘客在i列车后面的各班列车j>i上的分配量都不为零,当分配值Ak|ji小于0.5时,可以认为该时段内到达k站台的乘客在列车j出发时已分配结束.
据此,可以列出k站台各时段到达乘客在各班次列车上的分配数量表Ak,Ak|ji为该表中的第i行第j列数据值,含义为k站台,在时段[ti-2k,tik]内到达的乘客在列车j(j≥i)上的分配数量.
还可以列出k站台各时段到达乘客在各班次列车出发后剩余乘客数量表A′k,A′k|ji为该表中的第i行第j列数据值,含义为k站台,在时段[ti-2k,tik]内到达的乘客在列车j(j≥i)离开站台后剩下的乘客数量.
基于该模型,可以很容易地建立各班列车从各站出发时的载客量Nj发k及满载率γjk、站台上车比例φjk、各时段进站乘客的平均等待时间W[t1,t2]k等参数的计算表达式.需要说明,本模型认为站台k前若干班次列车出发滞留下的乘客与新到达的乘客是混合均匀以相同的上车比例上车的,这是比较符合实际情况(站台无特别的候车组织措施)的.
2.3 基于站台—列车客流交互预测模型的算法
步骤1:运算初始化,①根据前述已知条件计算任一列车j从任一站台k出发时刻tik(k=1,2,…,m.全线路共m个站点运营);②各班次列车依次抵达线路上第一个站台时车上载客量Nj到1(j=1,2,…,l.全天共l班列车运营);③各班次列车在第一个站台的下客量Xji=0;④列车1在站1上一时段滞留量Z01=0;⑤任一列车j空驶时的最大容纳能力为Cj(j=1,2,…,l);⑥制定任一站点k的OD 比例表Bk,Bk|ji为该表中的第i行第j列数据值,含义为k站台,在时段[ti-1k,tik]内进入站台的乘客在站j下车的分配比例.
步骤2:以列车1为跟踪对象,依列车1到达站台的次序逐个计算及运行参数Nk1发 ,γk1,φk1的计算过程如下所示:将φ11代入表A1→计算A1|11→计算X12→计算φ12→将φ12代入表A2→计算A2|11→计算X13→计算φ13…依次类推,直至计算完φk1(k=1,2,…,m.),此时运行参数Nk1发 ,γk1也全部计算得到.其中关键中间参数
步骤3:以列车2为跟踪对象,依列车2到达站台的次序逐个计算φ2k及运行参数的计算过程和步骤2 类似.其中关键中间参数以此类推:
步骤i:以列车j为跟踪对象,依列车j到达站台的次序逐个计算φjk及运行参数Nj发k,γjk,φjk的计算顺序和前面类似.其中关键中间参数计算完列车l的所有运行参数后,计算结束.
从上述各参数的计算过程可以看出,计算的每一步,都是以每一班列车依次从沿线每一站台出发时刻为时间节点,列车停站期间的计算中只需要该时间节点前的乘客到达规律,与该时间节点后的到达规律无关,各参数所需要的中间参数也能在每一步计算中得到,所以,本算法满足实时性要求.
3 计算实例
如图1所示运行方向的线路上,有站1~站5五个站点,站台到达率分别为2人·s-1,3人·s-1,2人·s-1,2人·s-1,均为平均分布,区间运行时间为5min,发车间隔为10min,列车停站时间为30s,列车最大容纳能力Cj=2 600人,列车定员数为1 900人.记时刻0为各站点开始运营时间,各班车抵达站1所需时间为2 min.各站台进站乘客分时段动态OD 分布比例见表1.限于篇幅,本实例只计算前10班车的运行情况.计算结果见表2~表3.
图1 计算实例Fig.1 Calculation example

表1 各站OD 分布Tab.1 Passengers’OD distribution of every station
(1)各班列车停站期间各站站台的乘客上车比例(φjk),见表2.

表2 各班列车在各站台的乘客上车比例Tab.2 Passengers’getting-on rate
(2)各站在[t1k,t2k]时段内(k=1~4)到达站台的乘客的平均等待时间分别为300,356,446,305s.
(3)各班列车从各站站台出发时的满载率(γjk)见表3.
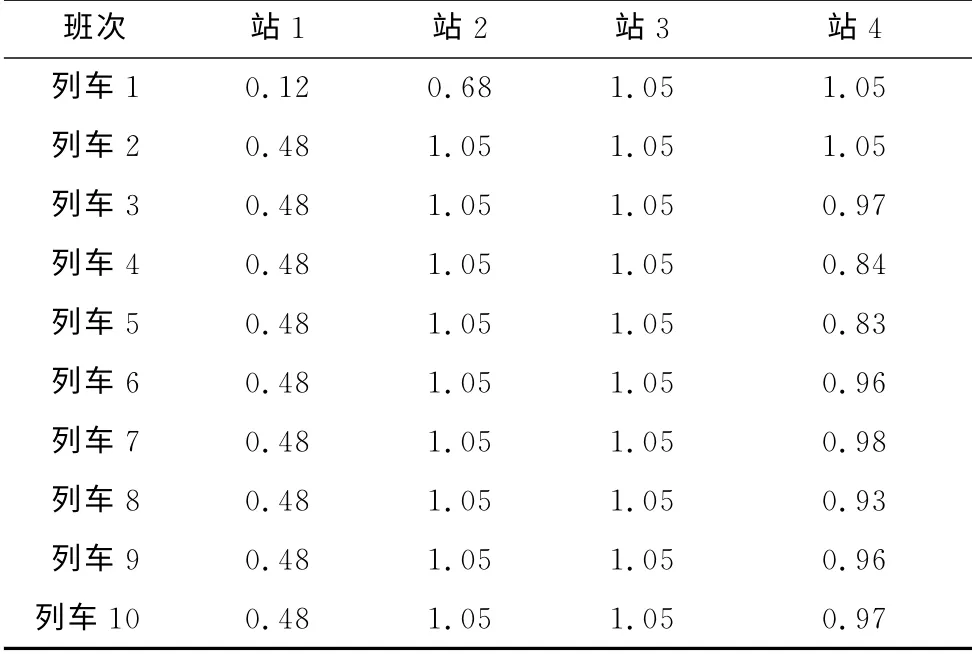
表3 列车满载率Tab.3 Occupancy rate of each train
(4)00:20:00~01:00:00内断面S1~S4的流量分别为4 800,10 400,10 400,9 687人.
4 结束语
当多条轨道交通线路相交而构成网络时,网络中各线路各班次列车到达换乘站后,要改变该站点相应换乘站台的客流到达函数,需要解决各列车抵达换乘站后如何改变相应站台客流到达函数的问题.因此,网络运营条件下的客流实时分布算法比单条线路的算法更加复杂,需要另文阐述,但是网络计算中每条线路采用的算法正是单线算法,换乘客流的影响也是基于单线算法得来.所以,本文重点讲述的单线算法也是轨道交通网络运营条件下客流分布实时计算的基础.
城市轨道交通网络客流分布状况的实时预测,可以成为运营管理部门对轨道交通运营计划进行实时调整的依据,也有助于出行者了解自己预定出行计划的便捷性,以便及时地调整交通方式、出行路径.由于轨道交通网络客流分布实时预测涉及到的参数众多,相互影响,笔者对这些复杂的联系进行了深入的解析,解决了各站台不同时段到达的乘客在各班次列车上的分配及在站台滞留情况(基于站台—列车客流交互的预测模型)、网络条件下进站乘客OD 分布预测等关键问题,提出了基于站台—列车客流交互预测模型的实时算法,文中的实例说明了该算法的有效性、切实可行性.
[1] 朱顺应,郭志勇,邵春福.城市轨道交通规划与管理[M].南京:东南大学出版社,2008.ZHU Shunying,GUO Zhiyong,SHAO Chunfu.Urban rail transit planning and management [M].Nanjing:Southeast University Press,2008.
[2] 吴倩,晏启鹏.城市轨道交通客流预测模型研究[D].成都.西南交通大学交通运输学院,2007.WU Qian,YAN Qipeng.Study on models of the passengers flow prediction of urban rail transportation[D].Chengdu:Southwest Jiaotong University. School of Traffic and Transportation,2007.
[3] 刘倩,张冬泉.城市轨道交通客流诱导系统的研究与实现[D].北京.北京交通大学机械与电子控制工程学院,2009.LIU Qian, ZHANG Dongquan. The research and implementation of guidance system of passenger flow on urban rail transit[D].Beijing.Beijing Jiaotong University.School of Mechanical,Electronic and Control Engineering,2009.
[4] 孙松伟,易思蓉.城市轨道交通客流预测模型及方法研究[D].成都.西南交通大学交通运输学院,2008.SUN Songwei,YI Sirong.The prediction model and method research of urban railway transportation flow[D].Chengdu:Southwest Jiaotong University. School of Traffic and Transportation,2008.
[5] 吴祥云,刘灿齐.轨道交通客流量均衡分配模型与算法[J],同济大学学报:自然科学版,2004,32(9):1158.WU Xiangyun,LIU Canqi.Traffic equilibriumassignment model specially for urban railway network [J].Journal of Tongji University:Natural Sciece,2004,32(9):1158.
[6] 徐瑞华,罗钦,高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究[J].铁道学报,2009,31(2):110.XU Rui hua,LUO Qin,GAO Peng.Passenger flow distribution model and algorithm for urban rail transit network based on multi-route choice[J].Journal of the China Railway Society,2009,31(2):110.

