中国股票市场自组织临界性与对数周期幂律的实证研究

方 勇

（1.上海财经大学 应用经济学博士后流动站，上海 200433；2.上海金融学院 应用数学系，上海 201209）

中国股票市场自组织临界性与对数周期幂律的实证研究

方 勇1,2

（1.上海财经大学 应用经济学博士后流动站，上海 200433；2.上海金融学院 应用数学系，上海 201209）

文章沿袭金融物理学的研究思路和框架，选取上证指数1990年12月19日至2010年3月22日的日收盘价和日收益率作为样本数据，对中国股票市场的自组织临界性和对数周期幂律进行了实证研究。

自组织临界性；相变；对数周期幂律；金融物理学；投机泡沫；崩盘

目前，国内在行为金融学和演化博弈论研究领域已取得了很大的进展，研究文献大量出现，但在金融物理学领域的研究还刚刚起步，研究文献还不多见。本文将沿袭金融物理学的研究思路和框架，对中国股票市场的自组织临界性和对数周期幂律进行实证研究。

1 实证分析

1.1 样本数据

本文选取上证指数从1990年12月19日至2010年3月22日的日收盘价Pt和日收益率Rt作为样本数据，日收盘价和日收益率的样本容量分别为4720和4719。样本数据来源于RESSET金融研究数据库（http://www.resset.cn）。

1.2 泡沫与反泡沫的LPPL拟合

上证指数日收盘价时间序列Pt（t=1～4720）的演化如图1所示。将整个样本期分为14个阶段，包括7个市场上升期和7个市场下跌期。这里需要指出的是，1995年5月18日至1995年5月22日，由于受到管理层关闭国债期货消息的影响，在三个交易日内，上证指数就从582点暴涨到926点，涨幅高达59.11%。由于这三天的上涨行情是由突发事件的刺激引起的，所以没有考虑这三天的价格演化。表1列出了这13个不同阶段的时窗选择、时窗长度、价格区间及涨跌幅。图1和表1中的数据都明显地反映了中国股市作为一个新兴的不成熟的市场所具备的一个主要特征：暴涨暴跌。

Sornette,Johansen和Bouchaud（1996）[1]通过将股市崩盘与材料断裂进行类比，发现泡沫在趋向崩盘的过程中呈现出临界行为和对数周期振荡特征，并采用对数周期幂律模型（LPPL）来刻画泡沫的演化过程。他们认为，泡沫的形成是由于交易者之间相互模仿，通过正反馈形成集体效应，最终的崩盘是由市场动力学机制所致。LPPL模型为

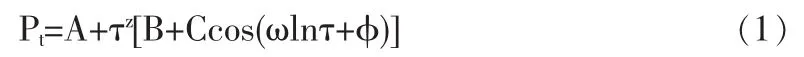
其中，τ=|tc-t|，tc是临界值，表示最有可能的崩盘时间 ，A,z,tc,B,C,ω,φ 均 待估 计 。 Johansen 和 Sornette（1999）[2]最早提出了反泡沫的概念，并在20世纪80年代的黄金价格和90年代的日本日经指数中找到了证据。Zhou 和 Sornette（2003）[3]首次发现了反转泡沫的存在。

运用Levenberg-Marquardt通用全局优化算法分别对上述14个子样本进行如 （1）式所示的LPPL拟合， 未知参数值的先验约束为：A＞0，z∈[0.2,0.8]，ω∈[5,15]，φ∈[0,2π]。各未知参数的估计值和拟合优度列在表2中，部分子样本的拟合结果如图2所示。14个子样本期的价格演化属性列在表1的最后一列，其中第 1，12，14个子样本期的价格演化属于泡沫，第3，5，8，10个子样本期的价格演化属于反转泡沫，第4，6，7，9，11，13 个子样本期的价格演化属于反泡沫，值得注意的是，我们发现了一个新的价格演化特性：第2个子样本期的价格演化属于反转反泡沫。

1.3 粗粒持续损失的扩展指数函数拟合

上证指数1990年12月20日至2010年3月22日的日收益率Rt的演化如图3所示，其描述性统计量列在表3中。从图3和表3可以看出，上证指数的日收益率时间序列显著地偏离正态分布，具有明显的波动聚集与尖峰厚尾特性。

考虑到时间序列含有噪声，这里考虑粗粒持续损失。设上证指数日收盘价时间序列{Pt:t=1～4720}有一个子序列 {Pt:t=a～b}，Pa是一个局部最大价格，Pb是一个局部最小价格，这个过程可能含有若干个持续上升子过程，若每个持续上升子过程的持续收益均不大于一个给定的阈值ε，则定义过程{Pt:t=a～b}的粗粒持续损失（也称为持续损失）为

将崩盘定义为最大的四个粗粒持续损失。现关于粗粒持续损失提出以下几个假设：

H1:粗粒持续损失满足如下式所示的扩展指数函数（幂律分布）

其中，N(|x|)表示粗粒持续损失不大于x(x＜0)的累积频数；A,b,z均大于0，是待估的参数；z反映了幂律分布的厚尾特性，z越小，幂律分布的尾部越厚。

H2:崩盘是幂律分布的异常点。

H3:崩盘的产生源于三种途径：紧随LPPL泡沫或反转泡沫之后；产生于LPPL反泡沫或反转反泡沫过程中；源于外生的冲击。

表1 不同阶段上证指数日收盘价格的演化特性

表2 不同阶段LPPL拟合的参数估计和拟合优度

运用上证指数的日收益率样本数据对上述三个假设进行检验。

对粗粒持续损失进行如 （3）式所示的扩展指数函数拟合，但是为了拟合的稳健性，对（3）式的变形

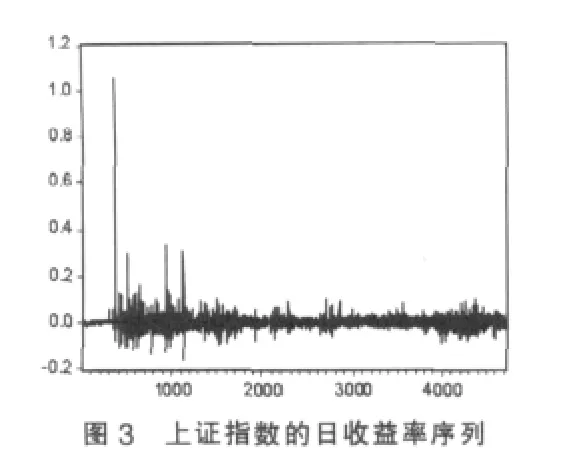
表3 上证指数日收益率序列的描述性统计量

表4 扩展指数函数拟合的参数估计与拟合优度

表5 崩盘的属性及触发事件

进行拟合。设日收益率样本标准差为σ，阈值分别取为0和0.5σ。拟合的参数估计值和拟合优度列在表4中。拟合结果表明，假设H1是成立的。

ε=0和ε=0.5σ时粗粒持续损失的幂律拟合图及拟合残差图分别如图4和图5所示。残差图中的两条水平直线代表正负两倍的残差标准差，如果某个残差的绝对值大于两倍的残差标准差，则将与其相对应的样本数据判定为异常点。从图4中的拟合残差图可以看出，当ε=0时，在四个崩盘中，第一个和第二个最大持续损失是异常点，而第三个和第四个最大持续损失不是异常点。从图5中的拟合残差图可以看出，当ε=0.5σ时，四个崩盘均是异常点。因此，两个拟合残差图表明，对我们的样本数据而言，假设H2基本上是成立的4。

表5列出了当ε=0和ε=0.5σ时四个崩盘的属性及触发事件，结果表明，假设H3是成立的。另外，当ε=0和ε=0.5σ时，四个崩盘均发生在1992年至1996年期间，在这个期间，中国股票市场还刚刚起步，极端不成熟，“政策市”特征明显，“暴涨暴跌”成为这个时期的主要特征。

2 结论

本文沿袭金融物理学的研究思路和框架，选取上证指数1990年12月19日至2010年3月22日的日收盘价和日收益率作为样本数据，对中国股票市场的自组织临界性和对数周期幂律进行实证研究。

首先，将整个样本期分为14个阶段，包括7个市场上升期和7个市场下跌期，分别在这14个时期对上证指数日收盘价进行LPPL拟合。拟合结果表明，第1，12，14个子样本期的价格演化属于泡沫，第3，5，8，10个子样本期的价格演化属于反转泡沫，第 4，6，7，9，11，13 个子样本期的价格演化属于反泡沫，值得注意的是，我们发现了一个新的价格演化特性：第2个子样本期的价格演化属于反转反泡沫。

其次，分别考察ε=0和ε=0.5σ时的粗粒持续损失，将崩盘定义为最大的四个粗粒持续损失，并运用样本数据对关于粗粒持续损失的三个假设进行了检验。结果显示，对于中国股票市场而言，上述三个假设均是基本成立的。

实证数据分析表明，中国股票市场还是一个新兴的不成熟的市场，“政策市”特征和“暴涨暴跌”特征明显。因此，研究自组织临界性和对数周期幂律对于危机的预警和控制具有重要而深远的意义。

[1]Sornette D,Johansen A,Bouchaud J P.Stock Market Crashes,Precursors and Replicas[J].Journal of Physics in France,1996,6.

[2]Johansen A,Sornette D.Financial Anti-Bubbles:Log-Periodicity in Gold and Nikkei Collapses[J].International Journal of Modern Physics C,1999,10.

[3]Zhou W X,Sornette D.Evidence of a Worldwide Stock Market Log-Periodic Anti-Bubble Since Mid-2000[J].Physica A,2003,330.

[4]GnacinskiP,Makowiec D.Another Type ofLog-Periodic Oscillations on Polish Stock Market[J].Physica A,2004,344.

F830.91

A

1002-6487（2011）10-0036-03

中国博士后科学基金资助项目（20090450075）；上海市自然科学基金资助项目（09ZR1421900）；上海市教育委员会科研创新资助项目（10YZ184）；上海市教育委员会重点学科建设资助项目（J51601）

方 勇（1972-），男，湖北黄冈人，博士，副教授，研究方向：金融统计与风险管理。

（责任编辑/易永生）