第一性原理方法预测水相核酸碱基及其代谢物的氧化还原电动势
李敏杰 刘卫霞 彭淳容 陆文聪
(上海大学化学系,上海200444)
1 Introduction
Ionizing radiation,photosensitization,or various oxidants are believed to be responsible for oxidatively generated damage to DNA.The reason is attributed to oxidative processes involving loss of an electron and the concomitant generation of a radical cation that migrates along the nucleobases of the du-plex by ahopping mechanism.1-10Low-energy electrons (LEEs)produced in significant numbers by ionizing radiation can also lead to DNA strand breaks via capture of LEEs to form radical anions.11-15Redox potentials of compounds in solution are fundamental properties in determining the innumerable chemical and biological electron-transfer reactions.16The redox potentials of nucleobases and the metabolites in aqueous solution offer critical insight into the electron transfer in DNA caused by ionizing radiation,oxidizing agent,and LEEs.In addition,they are crucial for the design of new redox-active nucleobase compounds using DNA substituents as building blocks.6,17,18
Although considerable efforts have been devoted to the determination of the redox potentials of DNA and RNA constituents,only few have been reported.19-22And the experimental data reported by one group are different from those reported by other groups.23-34On one hand,different experimental conditions(such as solvent,pH,detection method,etc.)affect the experimental observations significantly.For example,Fukuzumi et al.29reported a redox potential of 1.42 V for deoxyadenosine in aqueous solution at pH 7,whereas Steenken and Jovanovic27observed 2.03 V at pH 1.On the other hand,unavoidable experimental uncertainties(such as irreversible electrochemistry, proton-coupled electron-transfer reaction,etc.)preclude the determination of redox potentials under well-defined equilibrium conditions.30,35,36Seidel et al.30measured the redox values of the DNA constituents under non-equilibrium irreversible conditions,which were known to be underestimated by ca 0.3 V compared to the standard ones recorded under reversible conditions.In this regard,debates still continue on the accuracy of the experimental redox potentials for the DNA and RNA substituents.35,36
In addition,limited theoretical work on redox potentials for DNA and RNA substituents in aqueous solution has been disclosed.Crespo-Hernández et al.37determined the redox potentials for DNA nucleosides and relevant nucleoside analogues in N,N-dimethylformamide or acetonitrile solutions using density functional theory and integral equation formulation of polarizable continuum model(IEFPCM)solvation model performed with the Gaussian 98 suite of programs.The difference between the calculated and the experimental oxidation potentials was found to be less than 0.3 V.37Baik et al.19predicted the oxidation potentials for DNA bases analogues in aqueous medium using PW91 functional and the conductor-like screening model for real solvents(COSMORS)solvation model implemented in the Amsterdam density functional package with the difference between the calculated and the experimental oxidation values greater than 0.38 V.
These experimental and theoretical results have contributed positively to the understanding of the electron transfer in DNA and RNA induced by loss of electrons or capture of LEEs.Nevertheless,they represent limited studies on the redox potentials of DNA and RNA substituents in aqueous medium.More importantly,the reported redox values were obtained under different experimental conditions and theoretical models.The differences of the reported redox potentials limit the applicability of the data.Hence,a unified set of redox potentials for DNA and RNAsubstituents in aqueous solution needs to be established.
This paper focuses on the one-electron redox potential calculations for nucleobases and the metabolites in aqueous solution.A first-principles theoretical protocol was developed to be the optimal for pH-dependent redox potential predictions in aqueous solution among eight theoretical models by comparing the theoretical predictions with the experimental data of 82 aromatic compounds.With this useful protocol we next predicted the redox potentials for nucleobases and the metabolites.Discussions were then made about interesting connections between the redox potentials and charge/electron transfer in DNA,and the impact of structural variations on redox potentials.
2 Computational details
All calculations were performed with the Gaussian 03 suite of programs.38Geometry optimizations in gas phase were performed using the B3LYP/6-31+G(d)method.Frequencies were calculated at the same level of theory for all the species to confirm the nature of the local minima and to obtain the zero-point energy(ZPE).Single-point electronic energies were then calculated at the B3LYP/6-311++G(2df,2p)levels.The free energy change was then computed including ZPE corrections,thermal corrections(0→298 K),and the entropy terms.All the calculated gas-phase free energies correspond to the reference state of 101325 Pa,298 K.
To calculate solvation energies,we used COSMORS model39at the HF/6-31+G(d)level(ε=78.39,radii=UAHF).Conductorlike polarizable continuum model(CPCM)model40at the HF/ 6-31+G(d)level was used for solution geometry re-optimizations(ε=78.39,radii=UAHF).All the free energies in aqueous solution reported in this paper correspond to the reference state of 1 mol·L-1,298 K.
3 Results and discussion
3.1 Developing a reliable protocol to calculate redox potential
3.1.1 Computing redox potentials in aqueous medium
From a free energy cycle as shown in Fig.1,the standard oxi-dation potentials(E⊖)can be calculated through the gas phase adiabatic ionization potentials(IP)and solvation energies using equation(1).
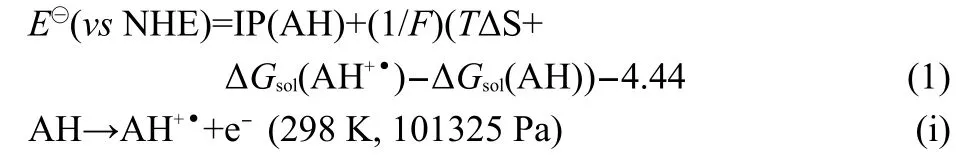
In equation(1),IP is the gas-phase adiabatic ionization potential(unit:eV),which is defined as the enthalpy changes of reaction(i).The second term,F is the Faraday constant,which equals to 23.06 kJ·mol-1·V-1.The next terms,TΔS(unit:kJ· mol-1)is the gas-phase entropy term of reaction(i).ΔGsol(AH+•) and ΔGsol(AH)(unit:kJ·mol-1),correspond to the solvation free energies of the reduced and oxidized forms in aqueous medium.The last term,-4.44(unit:V),is the free energy change associated with the reference normal hydrogen electrode (NHE)half-reaction(i.e.,H+(aq)+e-(g)→1/2H2(g)).22
In the same way,the standard reduction potential of reaction (ii)in aqueous medium can be computed using equation(2).

where,EA is the adiabatic electron affinity in gas phase(unit: eV),which is computed as the difference between the total energies of the appropriate neutral and anion species at their respective optimized geometries defined in the reaction.TΔS (unit:kJ·mol-1)is the gas-phase entropy term of the reaction. ΔGsol(AH-●)and ΔGsol(AH)(unit:kJ·mol-1)correspond to the solvation free energies of the reduced(anion)and oxidized (neutral)forms in aqueous medium.
3.1.2 Computing pH-dependent redox potentials in aqueous medium
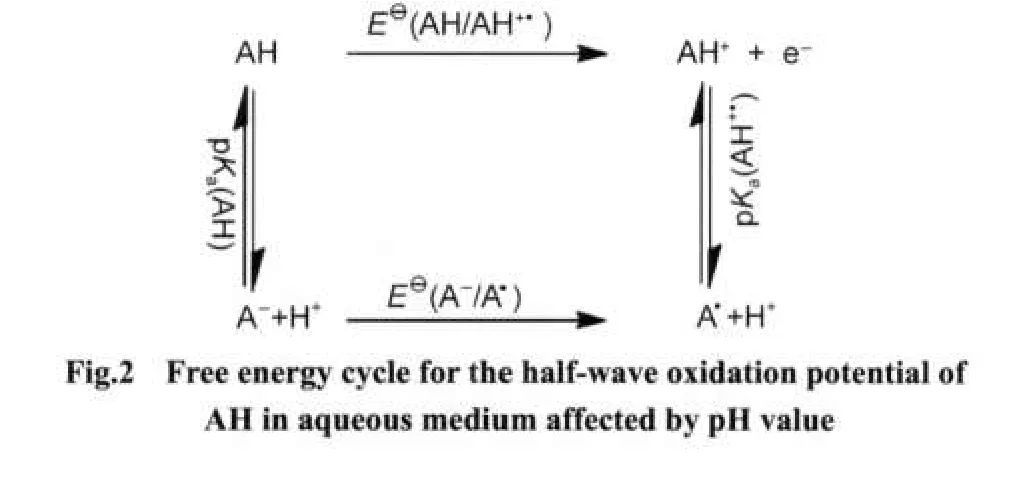
The redox potentials are highly pH dependent(decrease as pH increase)because of the rapid deprotonation of the corresponding radical cation at neutral(or basic)pH.6Nevertheless, none of the previous theoretical predictions took pH effects into consideration.From the following free energy cycle(Fig.2), oxidation potential can be computed at different pH values using equation(3).

where,Ka(AH+●)and Ka(AH)correspond to the acidity constant in aqueous medium,which can be computed from the following proton exchange reaction(iii)using equation(4).

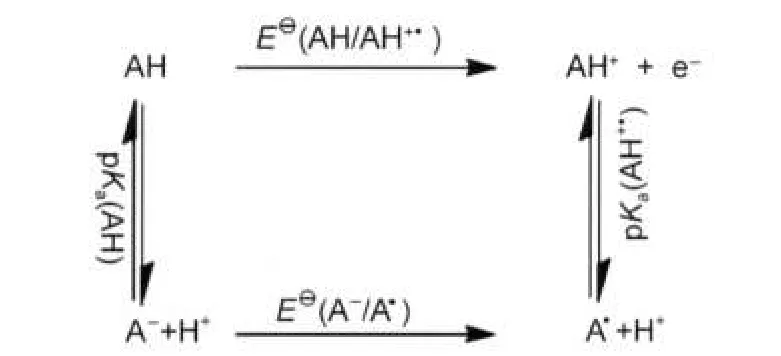
Fig.2 Free energy cycle for the half-wave oxidation potential of AH in aqueous medium affected by pH value

where,ΔGexchangeis defined as the solvation free energy change of the above reaction in aqueous solution.The experimental pKavalue for phenol is 9.98.41It was noteworthy that we chose phenol for the proton exchange reaction in that we wished to develop a most effective method for redox potential calculations of aromatic compounds.Likewise,reduction potential of reaction(ii)can also be computed at different pH values.
3.1.3 Evaluation of different theoretical protocols
We attempt to develop a reliable method to predict the redox potentials of aromatic compounds in aqueous medium.The gas-phase calculations were conducted using the standard B3LYP/6-311++G(2df,2p)//B3LYP/6-31+G(d)method which was tested for reliability in gas phase IP and EA calculations in previous studies.15The prediction accuracy of the redox potentials in aqueous solution relies heavily on the accuracy of the calculated solvation energies in the same solution.To select an appropriate solvation model,we tested the different solvation models for the calculation of the redox potentials in aqueous medium.
The CPCM solvation model with UAHF and UAKS cavity models at HF/6-31+G(d)level were used for re-optimized geometries in aqueous solution(ε=78.39).The COSMORS and CPCMsolvation models with UAHF and UAKS cavity models at the HF/6-31+G(d)level were used for solvation energies calculations for gas-phase and re-optimized solution geometries in aqueous solution.
The redox potentials in aqueous solution of 12 aromatic compounds containing phenol,aniline,and nucleobase analogues were predicted with 8 composite protocols(Table S1 in Supporting Information).Comparing the experimental data with the theoretical predictions,we find that the B3LYP/ 6-311++G(2df,2p)//B3LYP/6-31+G(d)in gas phase and the HF-COSMORS/UAHF for solvation energy calculations at the HF-CPCM/UAHF re-optimized solution geometries in aqueous solution protocol(method 1)is the most reliable theoretical protocol for predicting the redox potentials of aromatic compounds.The evaluation of different theoretical protocols was given in Table S2.
Using method 1,we also calculated the redox potentials of 70 aromatic compounds in aqueous solution.The results were summarized in Table S3.The experimental42-44and theoretical values of only several compounds were given in Table 1 for the other compounds with different substituent groups.It should be emphasized that several selected compounds have similar functional groups and heteroatoms as those in DNA constituents.In addition,their redox values extend over a wider range of potentials than those expected for the DNA and RNAsubstituents.
Comparing all the experimental redox potentials with theoretical predictions for the 82 compounds in Table S3,we found that the theoretical predictions were in good agreement with the experimental data.The correlation between the experimen-tal and theoretical redox potentials is shown in Fig.3.It can be seen from Fig.3 that the slope and intercept of the correlation are 1.00 and-0.003 V,respectively,indicating that there is almost no systematic error in the predictions.The correlation coefficient(r)is 0.977.The RMSD between the experimental and theoretical redox potentials is 0.124 V(e.g.12 kJ·mol-1) for 82 hetero-aromatic compounds.

Table 1 Experimental42-44and theoretical redox potentials(vs NHE,V)in aqueous solution for several compounds

Fig.3 Comparison between the theoretical and experimental redox potentials in aqueous solution
3.2 Determination of oxidation potentials for nucleobases and the metabolites
The above analysis demonstrates that method 1 can predict the redox potentials of hetero-aromatic compounds with a precision of about 0.124 V.Here we utilized this theoretical protocol to predict the oxidation potentials of nucleobases and 15 familiar metabolites in aqueous medium at pH 7.The oxidation values for nucleobases and the metabolites in neutral solution are listed in Table 2.
Table 2 clearly showed that oxidation potentials of purine nucleobases are lower than those of pyrimidine nucleobases. Guanine(G)has the lowest oxidation potential(1.10 V)among the five natural nucleobases,which show that guanine is the most commonly oxidized of the nucleobases.The oxidation value of adenine,1.38 V,is higher than that of guanine.The values of thymine,uracil,and cytosine were about 0.32,0.52, and 0.66 V higher than that of guanine,respectively.The data for DNA nucleobases follow the trend observed experimentally in solution:guanine<adenine<thymine<cytosine.34The order is also in agreement with the theoretical results predicted by Baik et al.19The relative electron-donating abilities in solution should decrease in the order of:purine nucleobases>pyrimidine nucleobases.

Table 2 Theoretical oxidation potentials(vs NHE,V)for nucleobases and the metabolites in aqueous solution
5-hydroxy-C has the lowest oxidation potential(0.53 V) among the five nucleobases and 15 familiar metabolites listed in Table 2,which is 0.57 V lower than that of guanine.Oxidation potentials of 5-hydroxy-U,8-oxoG,and 8-oxoA are 0.81, 0.87,and 1.00 V which are lower than that of guanine,respectively.Oxidation potentials of FAPy-G and FAPy-A are 1.09 and 1.17 V,which are comparable to that of guanine.Among the nucleobases and the metabolites,5-hydroxy-C and 5-hydroxy-U can be used as effective reductants for the design of new redox-active nucleobase compounds.
From Table 2,it is observed that the 5-hydroxyl group significantly reduces the oxidation potentials for pyrimidine metabolites,5-hydroxyl-C and 5-hydroxyl-U.The oxidation values of 5-hydroxyl derivatives are 1.23 and 0.81 V lower than those of cytosine and uracil respectively.Introduction of hydroxyl to 5-position of 5,6-dihydro-T and 5,6-dihydro-U similarly reduces the oxidation values for the 5-hydroxy derivatives.An opposite tendency is found that the 5-formyl group increases the oxidation potential noticeably for uracil metabolite,5-formyl-U. However,introduction of hydroxyl to 6-position of 5-hydroxy-5,6-dihydro-T and 5-hydroxy-5,6-dihydro-U has less influence on the oxidation values.These results indicate that introduction of different substituents to 5 and 6-positions has different effects on oxidation potentials for pyrimidine analogues, which can be explained by the spin density localized at 5-C and 6-C of the oxidized pyrimidines(see Table 3).The spin density on 5-C is much higher than that on 6-C in the oxidized pyrimidines.Thus,introduction of electron donating groups to 5-position of pyrimidines could significantly decrease the oxidation potentials.On the contrary,introduction of electron withdrawing groups to 5-position increases the oxidation potentials noticeably.Furthermore,additions to 5-position could have more significant effects on oxidation potentials than those to 6-position.

Table 3 Spin density distributions in the 5-and 6-positions of the oxidized and reduced pyrimidine nucleobases calculated at the B3LYP/6-31+G(d)level
Oxidation potentials increase markedly with the hydrogenation of carbon(5),carbon(6)double bond of thymine and uracil due to dearomaticity of ring systems.
The result reported in Table 3 suggests that 8-oxoG has a lower oxidation potential than that of guanine in aqueous solu-tion.26(a)Thus 8-oxoG is a better hole-trap than guanine.These predictions are in good agreement with experimental observations in aqueous solution by Steenken26(a)and Foote45et al.Likewise,8-oxoA is expected to have lower potential than that of guanine,which is in consistent with the observation reported by Baik et al.19

Table 4 Theoretical reduction potentials(vs NHE,V)for nucleobases and the metabolites in aqueous solution
The transfer direction of the hole,generated by one-electron oxidation in DNA,is an important topic for using DNA as building blocks for electronic devices.9,23,25,46,47Oxidation potential is intrinsically connected to hole-trapping ability of an agent.In our predictions listed in Table 2,oxidation potentials of 5-hydroxy-C,5-hydroxy-U,8-oxoG,and 8-oxoA are lower than that of guanine(G),which suggest that these four compounds are more powerful hole-trapping agents than guanine.
3.3 Determination of reduction potentials of nucleobases and the metabolites
Low electron affinities of nucleobases and limited accessible potential range(background discharge potential ca-1.7 V vs NHE)lead to limited experimental data on one electron reduction potentials.30Here,method 1 was used for reduction potential predictions of nucleobases and the metabolites(Table 4).
Uracil has the lowest reduction potential(2.05 V)in the five natural nucleobases.The reduction potential of thymine is 2.09 V,comparable to that of uracil.The value of cytosine is 0.10 V higher than that of thymine.The values of adenine and guanine are 0.41 V and 0.90 V higher than that of thymine.The reduction potentials for nucleobases increase in the order of:uracil<thymine<cytosine<adenine.Our results are consistent with Crespo-Hernández and co-workers'theoretical preditions.37Besides,our results are in good agreement with the experimental trend reported by Seidel et al.30
Reduction potentials for pyrimidine nucleobases are much lower than those for purine nucleobases.Our results suggest that thymine,cytosine and uracil are reduced by LEEs more easily than guanine and adenine.Pyrimidine nucleobases are found to have a stronger tendency to capture low-energy electrons than purine nucleobases.Thus the base-centered radical anions of the pyrimidine nucleotides might be the possible intermediates for DNA and RNA single-strand break.Our suggestions are in very good agreement with theoretical findings of Gu et al.12
In general,the reduction potentials of pyrimidine metabolites are much lower than those of purine counterparts.5-formyl-U has the lowest reduction potential(1.27 V)among the nucleobases and the metabolites(Table 4).The reduction potential(1.84 V)of 5-hydroxyhydantoin is higher than that of 5-formyl-U.The data of uridine glycol,5-hydroxy-C and thymine glycol are comparable to that of uracil.Of the nucleobases and the metabolites,5-hydroxy-U and 5-hydroxyhydantoin are the most effective oxidants for the design of new redox-active nucleobase compounds.
Table 4 clearly shows that introduction of 6-hydroxyl to 5-hydroxy-5,6-dihydro-T and 5-hydroxy-5,6-dihydro-U decreases the reduction potentials by 0.23 and 0.30 V,respectively.In comparison with cytosine and uracil,the reduction potentials of their 5-hydroxy analogs do not have obvious change. The rational explanations for the different changes in the reduction potential of pyrimidine analogues owe to the spin density localized at 5-C and 6-C of the reduced pyrimidines(see Table 3).The spin density on 6-C is much higher than that on 5-C in the reduced pyrimidines,which is the opposite of that in the oxidized forms.Therefore,introduction of hydroxyl to 6-position of pyrimidines could decrease the reduction potentials.Furthermore,introduction of 5-hydroxyl could have negligible effect on oxidation potentials.
Hydrogenation of carbon(5),carbon(6)double bond of thymine and uracil lead to the increase in the reduction potentials due to dearomaticity of ring systems,which has the same effect on the oxidation potentials.
In a word,our results indicate that electronic properties and structural variations of the aromatic rings of nucleobase metabolites have predictable impact on the reduction potentials.
4 Conclusions
We successfully developed a first-principles method to predict the pH-dependent redox potentials of aromatic compounds in aqueous medium with a RMSD of 0.124 V.Here,the B3LYP/6-311++G(2df,2p)//B3LYP/6-31+G(d)in gas phase and the HF-COSMORS/UAHF for solvation energy calculations at the HF-CPCM/UAHF re-optimized solution geometries in aqueous solution protocol is found to be the optimal method for predicting the redox potentials of aromatic compounds in aqueous solution.With this protocol,a set of redox potentials of nucleobases and the metabolites in aqueous medium were obtained.In addition,our observations about the impact of structural variations on redox potentials may provide important guidance in the design of new redox-active nucleobases compounds.
Although our calculations are directly relevant to free molecules in aqueous solution,they might be helpful in elucidation of the charge/electron transfer in nucleic acid.With an accurate knowledge of the redox potentials of H-bonded pairs in nucleic acid,an in-depth understanding of the charge/electron transfer in nucleic acid might be possible.In our further study,the reliable redox potentials for nucleoside base stacks and more complex nucleic acid system in aqueous solution will be determined and the discussion on the charge/electron transfer in nucleic acid will be made more thoroughly.
Supporting Information Available:Detailed geometrical coordinates optimized at the B3LYP/6-31+G(d)level of theory, and the evaluation of different theoretical method and the experimental and theoretical redox potentials of 82 compounds have been included.This material is available free of charge via the internet at http://www.whxb.pku.edu.cn.
(1) Steenken,S.;Telo,J.P.;Novais,H.M.;Candeias,L.P.J.Am. Chem.Soc.1992,114,4701.
(2) (a)Colson,A.O.;Sevilla,M.D.Int.J.Radiat.Biol.1995,67, 627. (b)Li,X.;Cai,Z.;Sevilla,M.D.J.Phys.Chem.B 2001,105, 10115. (c)Li,X.;Sevilla,M.D.;Sanche,L.J.Phys.Chem.B 2004, 108,5472. (d)Li,X.;Sanche,L.;Sevilla,M.D.J.Phys.Chem.B 2004, 108,19013.
(3) Desfrancois,D.;Abdoul-Carime,H.;Schermann,J.P.J.Chem. Phys.1996,104,7792.
(4) Huels,M.A.;Hahndorf,I.;Illengerger,E.;Sanche,L.J.Chem. Phys.1998,108,1309.
(5) (a)Li,M.J.;Liu,L.;Wei,K.;Fu,Y.;Guo,Q.X.J.Phys.Chem. B 2006,110,13582. (b)Li,M.J.;Liu,L.;Fu,Y.;Guo,Q.X.J.Phys.Chem.B 2005, 109,13818.
(6) Burrows,C.J.;Muller,J.G.Chem.Rev.1998,98,1109.
(7) Kelley,S.O.;Barton,J.K.Science 1999,283,375.
(8) Berlin,Y.A.;Burin,A.L.;Ratner,M.A.J.Am.Chem.Soc. 2001,123,260.
(9)(a)Giese,B.;Amaudrut,J.;Köhler,A.K.;Spormann,M.; Wessely,S.Nature 2001,412,318. (b)Giese,B.Accounts Chem.Res.2000,33,631.
(10) (a)Anusiewicz,I.;Berdys-Kochanska,J.;Sobczyk,M.;Skurski, P.;Simons,J.J.Phys.Chem.A 2004,108,11381. (b)Anusiewicz,I.;Sobczyk,M.;Berdys-Kochanska,J.; Skurski,P.;Simons,J.J.Phys.Chem.A 2005,109,484.
(11) LaVerne,J.A.;Pimblott,S.M.Radiat.Res.1995,141,208.
(12) (a)Gu,J.D.;Xie,Y.M.;Schaefer,H.F.J.Am.Chem.Soc. 2005,127,1053. (b)Hou,R.;Gu,J.;Xie,Y.;Yi,X.;Schaefer,H.F.J.Phys. Chem.B 2005,109,22053. (c)Gu,J.D.;Xie,Y.M.;Schaefer,H.F.J.Am.Chem.Soc. 2006,128,1250. (d)Gu,J.D.;Xie,Y.M.;Schaefer,H.F.Nucleic Acids Res. 2007,35,5165. (e)Lyngdoh,R.H.D.;Schaefer,H.F.Accounts Chem.Res. 2009,42,563. (f)Jaeger H.M.and Schaefer,H.F.J.Phys.Chem.B 2009, 113,8142.
(13) Li,X.;Sevilla,M.D.;Sanche,L.J.Am.Chem.Soc.2003,125, 13668.
(14) (a)Berdys,J.;Anusiewicz,I.;Skurski,P.;Simons,J.J.Am. Chem.Soc.2004,126,6441. (b)Berdys,J.;Skurski,P.;Simons,J.J.Phys.Chem.B 2004, 108,5800.
(15) Hendricks,J.H.;Lyapustina,S.A.;de Clercq,H.L.;Bowen,K. H.J.Chem.Phys.1998,108,8.
(16)(a)Fu,Y.;Liu,L.;Yu,H.Z.;Wang,Y.M.;Guo,Q.X.J.Am. Chem.Soc.2005,127,7227. (b)Fu,Y.;Liu,L.;Wang,Y.M.;Li,J.N.;Yu,T.Q.;Guo,Q.X. J.Phys.Chem.A 2006,110,5874. (c)Feng,Y.;Liu,L.;Fang,Y.;Guo,Q.X.J.Phys.Chem.A 2002,106,11518.
(17)Abraham,J.;Gosh,A.K.;Schuster,G.B.J.Am.Chem.Soc. 2006,128,5346.
(18) Becker,D.;Sevilla,M.D.Adv.Radiat.Biol.1993,17,121.
(19) Baik,M.H.;Silverman,J.S.;Yang,I.V.;Ropp,P.A.;Szalai,V. A.;Yang,W.T.;Thorp,H.H.J.Phys.Chem.B 2001,105,6437.
(20) Baik,M.H.;Ziegler,T.;Schauer,C.K.J.Am.Chem.Soc.2000, 122,9143.
(21) Kettle,L.J.;Bates,S.P.;Mount,A.R.Phys.Chem.Chem. Phys.2000,2,195.
(22) Trasatti,S.Pure Appl.Chem.1986,58,955.
(23)(a)Kawai,K.;Wata,Y.;Ichinose,N.;Majima,T.Angew.Chem. Int.Edit.2000,39,4327. (b)Kawai,K.;Wata,Y.;Hara,M.;Tojo,S.;Majima,T.J.Am. Chem.Soc.2002,124,3586. (c)Kawai,K.;Takada,T.;Tojo,S.;Ichinose,N.;Majima,T. J.Am.Chem.Soc.2001,123,12688.
(24) (a)Caruso,T.;Carotenuto,M.;Vasca,E.;Peluso,A.J.Am. Chem.Soc.2005,127,15040. (b)Caruso,T.;Capobianco,A.;Peluso,A.J.Am.Chem.Soc. 2007,129,15347.
(25) (a)Lewis,F.D.Photochem.Photobiol.2005,81,65. (b)Lewis,F.D.;Letsinger,R.L.;Wasielewski,M.R.Accounts Chem.Res.2001,34,159.
(26) (a)Steenken,S.;Jovanovic,S.V.;Bietti,M.;Bernhard,K. J.Am.Chem.Soc.2000,122,2373. (b)Steenken,S.Biol.Chem.1997,378,1293. (c)Steenken,S.Chem.Rev.1989,89,503. (d)Jovanovic,S.V.;Simic,M.G.J.Phys.Chem.1986,90,974.
(27) Steenken,S.;Jovanovic,S.V.J.Am.Chem.Soc.1997,119,617.
(28) (a)Close,D.M.J.Phys.Chem.A 2004,108,10376. (b)Crespo-Hernández,C.E.;Arce,R.;Ishikawa,Y.;Gorb,L.; Leszczynski,J.;Close,D.M.J.Phys.Chem.A 2004,108, 6373. (c)Close,D.M.;Øhman,K.T.J.Phys.Chem.A 2008,112, 11207. (d)Close,D.M.J.Phys.Chem.A 2008,112,8411. (e)Close,D.M.;Crespo-Hernández,C.E.;Gorb,L.; Leszczynski,J.J.Phys.Chem.A 2006,110,7485.
(29)Fukuzumi,S.;Miyao,H.;Ohkubo,K.;Suenobu,T.J.Phys. Chem.A 2005,109,3285.
(30) Seidel,C.A.M.;Schulz,A.;Sauer,M.H.M.J.Phys.Chem. 1996,100,5541.
(31) Lecomte,J.P.;Kirsch-De Mesmaeker,A.;Kelly,J.M.;Tossi,A. B.;Görner,H.Photochem.Photobiol.1992,55,681.
(32) Langmaier,J.;Samec,Z.;Samcová,E.;Hobza,P.;Reha,D. J.Phys.Chem.B 2004,108,15896.
(33) Kittler,L.;Löber,G.;Gollmick,F.;Berg,H.J.Electroanal. Chem.1980,116,503.
(34) Oliveira-Brett,A.M.;Piedade,J.A.P.;Silva,L.A.;Diculescu, V.C.Anal.Biochem.2004,332,321.
(35) Guirado,G.;Fleming,C.N.;Lingenfelter,T.G.;Williams,M. L.;Zuihof,H.;Dinnocenzo,J.P.J.Am.Chem.Soc.2004,126, 14086.
(36)Fiebig,T.;Wan,C.;Zewail,A.H.Chem.Phys.Chem.2002,3, 781.
(37) Crespo-Hernández,C.E.;Close,D.M.;Gorb,L.;Leszczynski, J.J.Phys.Chem.B 2007,111,5386.
(38) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.et al.Gaussian 03, Revision C.02;Gaussian,Inc.:Wallingford,CT,2004.
(39) Klamt,A.;Schüürmann,G.J.Chem.Soc.Perkin Trans.1993,2, 799.
(40) (a)Barone,V.;Cossi,M.J.Phem.Chem.A 1998,102,1995. (b)Fu,Y.;Wang,H.J.;Chong,S.S.;Guo,Q.X.;Liu,L. J.Org.Chem.2009,74,810. (c)Fu,Y.;Liu,L.;Li,R.Q.;Liu,R.;Guo,Q.X.J.Am.Chem. Soc.2004,126,814.
(41) Liptak,D.;Gross,K.C.;Seybold,P.G.;Feldgus,S.;Shields,G. C.J.Am.Chem.Soc.2002,124,6421.
(42) Suatoni,J.C.;Snyder,R.E.;Clark,R.O.Anal.Chem.1961,33, 1894
(43) Faraggi,M.;Broitman,F.;Trent,J.B.;Klapper,M.H.J.Phys. Chem.1996,100,14751.
(44) Lias,S.G.;Bartmess,J.E.;Liebman,J.F.;Holmes,J.L.;Levin R.D.;Mallard,W.G.J.Phys.Chem.Ref.Data 1988,17,Suppl. 1.
(45) Prat,F.;Houk,K.N.;Foote,C.S.J.Am.Chem.Soc.1998,120, 845.
(46) Grinstaff,M.W.Angew.Chem.Int.Edit.1999,38,3629.
(47) Schuster,G.B.Accounts Chem.Res.2000,33,253.

