一种引入速率量测的三维变结构多模型算法*
张国栋,刘 忠,孙世岩
(海军工程大学电子工程学院,武汉 430033)
0 引言
反舰导弹从发射到命中,飞行时间短,飞行高度低,威力大,机动性能好,突防能力强,而且能够灵活的在空中、水面、水下发射,对我舰构成巨大威胁,同时对火控系统的跟踪性能提出了苛刻的要求。在机动目标跟踪领域,国内外许多学者做了大量的研究,其中VSMM算法不失为一种有效的解决方法。该方法由Li X R[1]和 Kirubarajan[2]等人所提出。实现VSMM最普遍的方法是递归自适应模型集合(RAMS)方法。主要由两部分功能组成:模型集合自适应(MSA)和模型集合序列条件估计。模型集合自适应的任务是确定每一时刻MM估计器使用哪个模型集合。Li X R设计了三种模型集合自适应方法:激活有向图(AD)方法、自适应网格(AG)方法和有向图切换(DS)方法。
文中通过对新息残差的自适应调整来实现模型集合自适应,属有向图切换法[3]。在进行模型集的设计时,针对现代观测雷达可以输出目标运动的距变率(径向速度)信息,并且可以由速率陀螺获得目标运动的角变率(角速率)信息的情况,通过附加速率观测通道,将速率量测值(包括距变率和角变率)引入各三维子模型中,探讨引入速率量测后VSMM算法性能的改善情况。
1 引入速率量测的VSMM算法
文中采用极坐标系下的量测模型和直角坐标系下的状态模型进行目标跟踪理论的研究。以我舰观测雷达为原点建立空间直角坐标系,则目标在直角坐标系内的运动情况如图1所示。
参照图1,假设目标在水平面内作匀速直线运动,r、φ、ε是观测雷达输出的斜距、方位角、俯仰角信息,则˙r、˙φ、˙ε是上述信息的变化率。设斜距、方位角、俯仰角的随机观测误差均方差分别为σr、σφ、σε,同时忽略系统误差。
假设初始速度和位置为零,极坐标系与直角坐标系之间的关系如下:

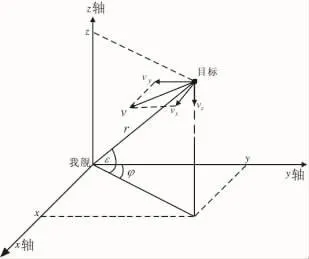
图1 火控滤波直角坐标系及目标运动情况
1.1 模型集合设计
由于目标作转弯机动时除了位置和速度信息的变化外,还存在着高低角和方位角信息的变化,并且测量信息在三维直角坐标系下是相互耦合的,因此传统VSMM算法对三维空间中目标的转弯机动跟踪效果较差,而对目标的匀速、匀加速机动跟踪效果较好。基于以上原因,文中模型集的设定将主要针对目标的转弯机动。设定以下9个模型集,模型集中包含各子模型:
模型集1:{CV跟踪模型;CA跟踪模型}
模型集2至模型集9为不同高低角变化率(0.05rad、0.1rad、0.15rad、0.2rad、-0.05rad、-0.1rad、-0.15rad、-0.2rad、)和 不 同 方 位 角 变 化 率 (0.05rad、0.1rad、-0.05rad、-0.1rad)的CT跟踪模型组合,每一个模型集里面包含4个不同高低角变化率和方位角变化率的CT跟踪模型。
上述模型集中,模型集1针对目标的直线运动,模型集2到9针对目标的曲线运动。各模型集中的子模型均为第2节介绍的引入速率量测三维跟踪模型。
1.2 机动检测准则设计
采用滑窗式[4]加权平方检测法作为机动检测准则。
定义距离函数:
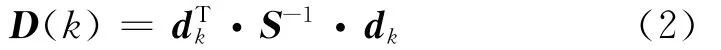
由新息序列的统计性质可知,D(k)服从自由度为m的χ2分布,其概率密度函数为:
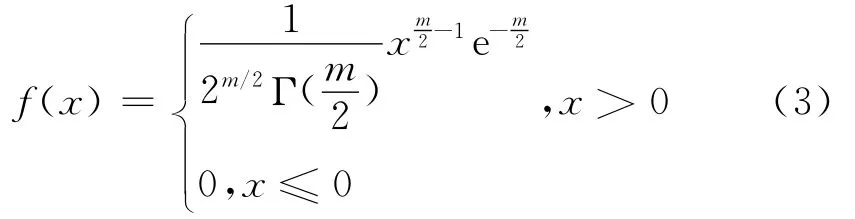
如果目标发生机动,新息d(k)将不再是均值为零的高斯白噪声随机过程,D(k)将会增大,因而可用下述方法检测机动的发生与消除:取D(k)大于某一门限M的概率为a,即:

式中:a为允许的虚警概率;当D(k)>M时,机动发生;当D(k)≤M时,机动消除。
根据文献[6],当概率为0.8时,窗口长度为5;χ2分布置信度0.95时,30自由度情况下门限值为43.773。
1.3 最佳模型集合选择准则设计
采用如下最佳模型集合选择准则:若模型集1的距离函数D(k)未超过给定阈值,则确定目标作直线运动,该集合为最佳模型集合;若模型集2到9中某一模型集的距离函数D(k)未超过给定阈值,则确定目标作曲线运动,该集合为最佳模型集合。
1.4 VSMM算法流程
1)初值选取
以观测系统输入的第一次观测值为滤波器的初值,滤波器从k=1开始工作。
2)算法描述
Step1:对VSMM进行初始化,输入初值X1、P1;
Step2:对各模型集进行IMM滤波;
Step3:判断出各模型集中新息残差最小的模型集a,输出模型集a的滤波结果;
Step4:更新量测值;
Step5:对模型集a进行IMM滤波,若滤波结果未检测到目标机动,则输出模型集a的滤波结果;若滤波结果检测到目标机动,则激活其它模型集,并利用a在k-1时刻的结果对各模型集进行重新初始化;
Step6:是否停止解算?是,结束;否则,转Step3。
2 引入速率量测的子模型设计
2.1 匀速直线运动(CV)目标跟踪模型
取卡尔曼线性状态方程和观测方程中各项为:
状态向量:
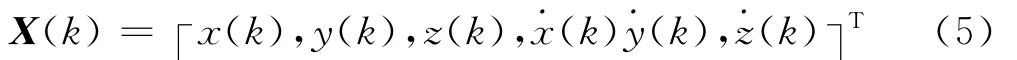
观测向量:
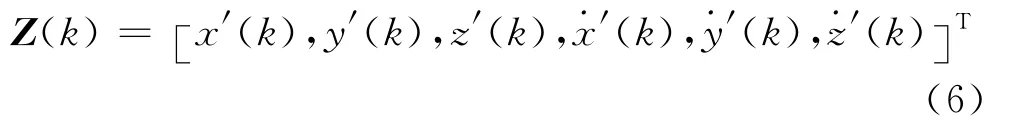
状态转移矩阵:

将观测雷达得到的球坐标系下的信息转换到直角坐标系下:
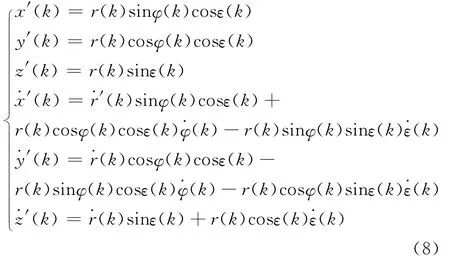
观测噪声V(k)是零均值、白色高斯过程噪声序列且相互独立,协方差为:
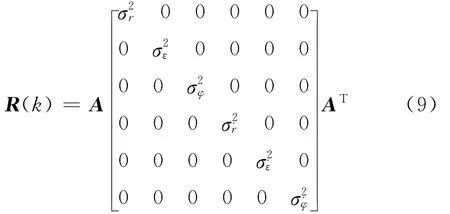
其中系数矩阵A为:

系统误差W(k)是零均值、白色高斯过程噪声序列,协方差为:
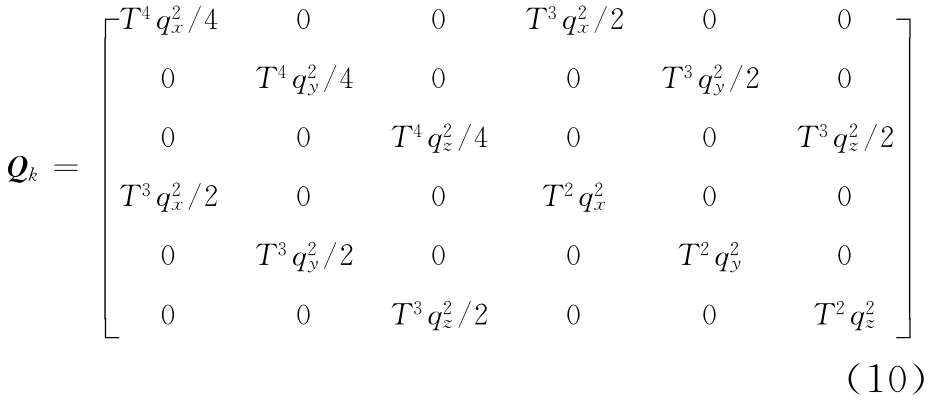
2.2 匀加速直线运动(CA)目标跟踪模型
在基于CV运动的滤波模型基础上,将状态向量进行扩维如下:
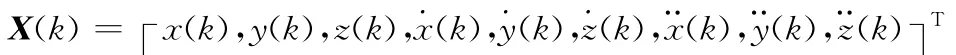
其余各项与CV跟踪模型基本相同,受篇幅限制,不作赘述。
2.3 匀速圆周运动(CT)目标跟踪模型
以x轴为例,三维空间下第k+1时刻目标的x轴位置分量可表示为:
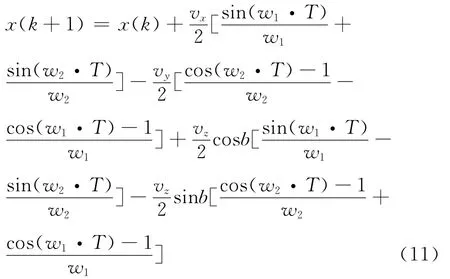
相应地,第k+1时刻目标的x轴速度分量可表示为:

取系统的状态向量为:
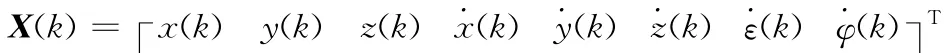
此时系统的状态方程非线性,不再符合标准卡尔曼滤波的要求,需要利用扩展卡尔曼滤波(EKF)方法,将非线性观测量在预测点处进行泰勒展开后舍去高次项,化为线性方程。
其余各项与CV跟踪模型基本相同,受篇幅限制,不作赘述。
3 仿真实现
为了验证文中所提算法的有效性,并且考察引入速率量测后对VSMM算法机动检测性能的影响,对传统VSMM算法(记为无速率量测VSMM)和文中所提算法(记为有速率量测VSMM)进行蒙特卡洛仿真实现,并计算滤波结果的均方根误差,从而比较各算法的跟踪性能。
3.1 仿真初始设定
设目标在三维空间内进行机动,航路特征为典型反舰导弹攻击航路。目标前10s在水平面作速度为850m/s的匀速直线运动,高度20m;10~55s在水平面作蛇形机动,降高到10m;55~60s在水平面作比例导引运动,垂直面作跃升俯冲运动。舰艇在高度为零的水平面作匀速直线运动。初始斜距22698m;雷达采样率50Hz;采样持续时间30s;观测距离随机误差5m;观测距变率随机误差2m/s;观测方位角、高低角随机误差0.9mrad;观测方位角、高低角变化率随机误差0.5mrad/s。
3.2 仿真结果

图2 目标运动轨迹及滤波效果模拟
图2~图4显示,速率量测的引入可明显改善基于新息χ2分布的VSMM算法的跟踪性能,并且在检测到目标机动后,有速率量测VSMM能够做到快速收敛,保持机动检测的稳定性和原先的算法收敛精度,这是无速率量测VSMM的机动检测算法所不具备的。
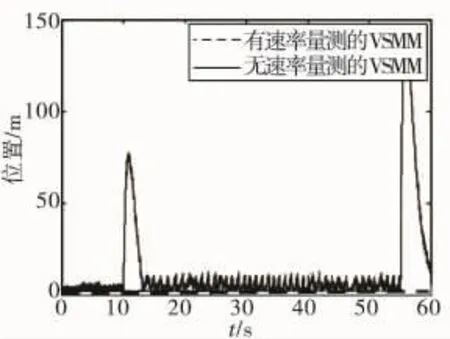
图3 两种算法位置滤波误差比较图
下面对两种算法的机动检测延时情况进行详细分析。
以目标作机动的时刻到算法检测到机动的时刻作为机动检测延时,经过50次蒙特卡洛仿真分析,可得结果见表1。
表1显示,有量测VSMM比无量测VSMM的检测延时要小很多。这是因为:滑动窗口内距离量D(k)需要累积一定数目的突变点才能检测到目标机动;同时有量测VSMM的D(k)计算还受速度分量影响,因此距离量D(k)的变化要比无量测VSMM快。
为进一步分析速率量测对算法机动检测延迟的影响,将有量测VSMM的距离量D(k)突变情况绘制成如图5~图6的图。

图5 目标在10s机动时的D(k)值
由图5、图6可知,在目标机动后的第三个采样 点 (0.06s)左右,距离量D(k)达到最大,算法检测到机动并切换模型集,因此在随后的3到4个采样点(0.06~0.08s)内D(k)值变小,机动检测消除。

图6 目标在55s机动时的D(k)值
4 结论
文中对可以观测距变率和角变率的雷达观测系统提出了一种引入速率量测的三维变结构多模型算法(VSMM)。仿真结果表明,速率量测的引入可显著改善VSMM算法的跟踪性能,并且可以提高对目标机动检测的稳定性,缩短检测延时。算法的上述优点可以明显减少火控系统的反应时间,从而使系统对空中目标的跟踪更为准确、迅速、稳定,具有一定工程实践指导意义。
[1]LI X R,Bar-Shalom Y.Multiple model estimation with variable structure[J].IEEE Transactions on Automatic Control,1996,24(1):478-493.
[2]Kirubarajan T,Bar-Shalom Y,Pattipatik P,et al.Ground target tracking with variable structure IMM estimator[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(1):26-44.
[3]A T Alouani,P Xia,T R Rice,et al.Two-stage Kalman estimator for tracking maneuvering targets[C]//Conf.Proc.1991IEEE International Conference on Systems,Man,and Cybernetics.Decision Aiding for Complex Systems,1991:761-766.
[4]范红旗,王胜,付强.目标机动检测算法综述[J].系统工程与电子技术,2009,31(5):1064-1070.
[5]石章松,谢君.机动检测算法特性分析仿真研究[J].计算机仿真,2007,24(9):90-94.
[6]Y Bar-Shalom,K BIRMIWAL.Variable dimension filter for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1982,AES-18(5):621-629.

