广义线性模型中拟似然估计的弱相合性及渐近正态性

王健发，肖泽青，王泸怡

（广西大学 数学与信息科学学院，广西 南宁 530004）

广义线性模型中拟似然估计的弱相合性及渐近正态性

王健发，肖泽青，王泸怡

（广西大学 数学与信息科学学院，广西 南宁 530004）

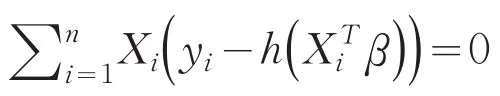
拟似然估计；弱相合性；渐近正态性

广义线性模型（GLMS）由Nelder和Wedderburn[1]引入，作为一种处理非正态响应变量的回归分析模型，其定义如下

其中yi是q维响应变量,Xi是p×q设计矩阵.h∶Rq→Rq是充分光滑的一一映射，β∈Rp是未知的回归参数，β0是它的真值，函数h的逆称为联系函数.给定Xi的条件下，yi( )i=1,…,n独立且有如下的指数分布：

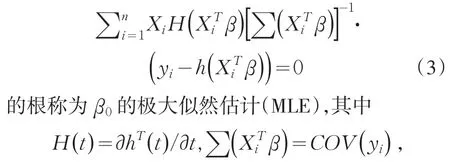
其中：θi称为自然参数；b()·,c()·为相应于指数分布的确定函数.对数似然方程由b(·)和h(·)可求得 ∑(·).在许多情形下假定yi服从指数分布（2）是不切实际的，而且∑(·)的确切表达式不知道.但如果期望（1）假定是正确的，我们仍可用Wedderburm引入的拟似然方法，用拟似然方程

1 主要结果

2 定理的证明

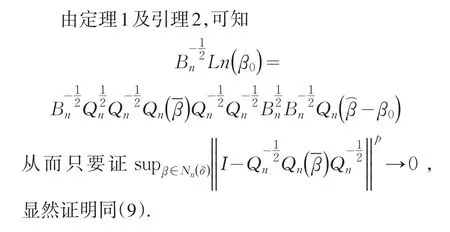
[1]Nelder J A,Wedderburn RWM.Generalized linear model[J].J Roy Statist Soc Ser A,1972,135(3):370-384.

[2]Fahrmeir L,Kanfmann H.Comsistency and asymptotic normality of the maximum likelihood estimator in general⁃ized linear regression[J].Ann Statist,1985,13,342-236.

[3]Chen K,et al.Strong consistency of maximum Quasi-like⁃lihood estimators in generalized linear models with fixed and adaptive design[J].Ann Statist,1999,27,1155-1166.

[4]Yue L,Chen X R.Rate of strong consistency of qua⁃si-maximum likelihood estimate in generalized linear mod⁃els[J].Science in China Series A-Mathematics,2004,47(6):882-893.

[5]赵林城,尹长明.广义线性模型中极大拟似然估计的强相合性[J].中国科学A辑:数学,2005,5(3):312-317.

[6]尹长明,赵林城.广义线性模型中极大拟似然估计的渐进正态性与强相合性[J].中国科学A辑:数学,2005,35(11):1236-1250.

[7]高启兵,吴耀华.广义线性回归拟似然估计的强相合性[J].数学年刊:A辑,2004,25(6):705-710.

[8]Liang K Y,Zeger S L.Longitudinal data analysis using gen⁃eralized linear models[J].Biometrika,1986,73(1):13-22.

[9]张三国,廖源.关于广义线性模型拟似然估计弱相合性的几个问题[J].中国科学A辑:数学,2007,37(11):1368-1376.

[10]戴牧民,陈武华,张更荣.实分析与泛函分析[M].北京:科学出版社,2007:28.

[11]Liao Y.Weak consistency of quasi-maximum likelihood estimates in multivaiate generalized linear models[J].Chi⁃nese Journal of Applied Probability and Statistics,2006,22(3):288-294.

Weak Consistency and Asymptotic Normality of Quasi-Maximum Likelihood Estimates in Generalized Linear Models

WANG Jianfa，XIAO Zeqing，WANG Luyi
（School of Mathematics and Information Science，Guangxi University，Nanning530004，China）

In a generalized linear model withq×1 responses,bounded and fixedp×qregressorsXiand natural link func⁃tion,we study the solutionof quasi-maximum likelihood equationand other conditions,and use contractive mappings to prove that the quasi-likelihood equation has a solutionof weak consistency;Fort＞0,let ψ(t) be a positive nondecreasing function such thatis a convex function,which prove the asymptotic normality of maximum quasi-likehood estimatorβn.

quasi-maximum likelihood estimation；weak consistency；asymptotic normality

O 212.1

A

1674-4942（2011）02-0137-04

2011-01-25

国家自然科学基金（11061002）

毕和平