任意两斜方向间角应变的一个公式
王岷,张岭,张莉辉
(河北大学建筑工程学院,河北保定 071002)
任意两斜方向间角应变的一个公式
王岷,张岭,张莉辉
(河北大学建筑工程学院,河北保定 071002)
基于连续介质力学随体导数的概念,以随体微分代之以随体导数,应用于弹性体应变分析中,得出了弹性体任意两斜方向间角应变的一个公式,并对该公式的正确性进行了验证.
弹性体;随体导数;随体微分;斜方向;角应变
弹性体的变形可归结为用任意两点间线段长度的改变和任意两线段间相对夹角的改变来表征,为了叙述方便,在小变形的前提下,将线段间夹角的改变也称作角应变.
关于弹性体的应变分析已有非常系统的理论和结果,但相对来讲,还有待进一步完善[1].关于任意两斜方向上的角应变分析,许多文献都有类似的讨论,结果也大致相同,公式的形式应用起来不是十分方便[2-5].
由于考察弹性体变形时不必考虑时间效应,本文借鉴文献[6]的方法,以随体微分代之以随体导数,应用于弹性体应变分析中,给出了弹性体任意两斜方向间角应变的一个公式,并对该公式的正确性进行了验证.此公式形式简单,应用起来相对比较方便、容易.
1 弹性体的位移和变形

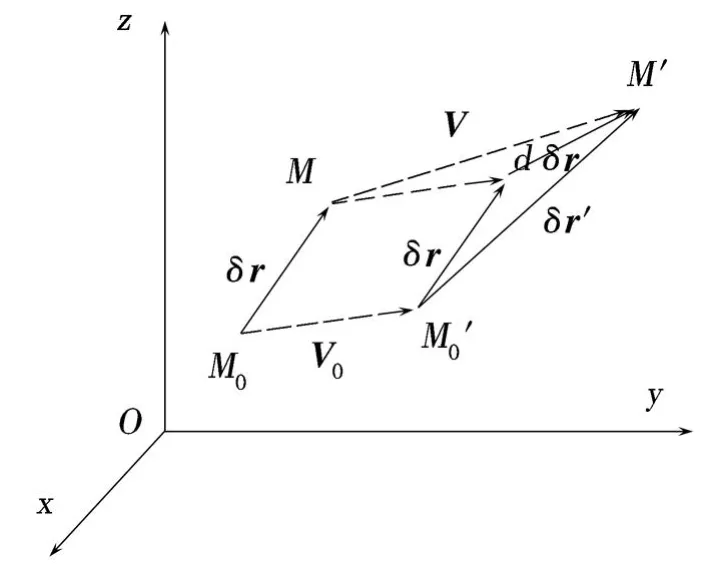
图1 弹性体的位移和变形Fig.1 Displacement and deformation of an elastic body


称为线元δr随体微分.
记δV=V-V0,易见

将M点的位移V在M0点Tay lor展开,略去高阶项,有

2 任意两斜方向间的角应变
由式(3)和式(4),得

在M0点沿任意两单位斜方向 N1=(l1,m1,n1),N2=(l2,m2,n2),取两物质线元δr1和δr2,则有


其中I=δij为单位张量,θ12即任意两斜方向N1和N2之间的角应变,以减小为正,反之为负,εN1,εN2分别为N1和N2方向的线应变.
N1×N2≠0时,式(10)可改写为

式(11)即任意两斜方向N1=(l1,m1,n1),N2=(l2,m2,n2)间角应变公式.
3 讨论
为了说明结果的正确性,从公式(9)出发做如下讨论:
1)N1=N2=N时,|N1×N2|=0,N1·N2=1,由式(9)得到εN=N·S·N,即得到任意 N=(lmn)方向线元的线应变公式

于是,得到任意两正交线元间的角应变公式

若取[N1,N2]分别为[i,j],[j,k]和[k,i]时,θ12即分别为γxy,γyz和γzx.可见公式(11)是正确的.
4 结论
以上讨论表明公式(9)是正确的,同时也验证了任意两斜方向间角应变公式(11)的正确性.公式(11)的形式比较简单,应用起来相对比较便利、容易,但对于有限变形此公式不适用.
[1]严宗达.建议一个角应变的新定义[J].应用数学和力学,1984,5(1):103-109.
[2]徐芝纶.弹性力学:上册[M].北京:高等教育出版社,2006.
[3]吴家龙.弹性力学[M].北京:高等教育出版社,2004.
[4]TIMOSHENKO S P,GOOD IER J N.Theory of elasticity[M].Beijing:Tsinghua University Press,2004:15-33.
[5]UGURAL,A C,FENSTER S K.Advanced strength and app lied elasticity[M].Upper Saddle River,N J:Prentice Hall PTR,2003.
[6]吴望一.流体力学[M].北京:北京大学出版社,2005.
Formula of Shear Strain Between Two Arbitrary Oblique Directions
WANGMin,ZHANGLing,ZHANGLi-hui
(College of Civil Engineering and A rchitecture,Hebei University,Baoding 071002,China)
Based on the concep t of material derivative for continuum mechanics,usingmaterial differential in p lace of material derivative and applying it to strain analysisof the elasticity solid,a formula of shear strain between two arbitrary oblique directions in the elastic body wasobtained,the accuracy of the formula was also verified.
elastic body;material derivative;material differential;oblique direction;shear strain
O 343.5
A
1000-1565(2011)04-0352-04
2010-09-20
河北省教育厅科研基金资助项目(2005128)
王岷(1965-),男,河北保定人,河北大学教授,主要从事应用数学与力学方面的研究.
E-mail:wangmin@hbu.edu.cn
王兰英)

