基于Matlab的匀质摆杆所受转轴约束力分析

肖长江，王晓磊，魏 勇

（燕山大学里仁学院，河北秦皇岛 066004）

基于Matlab的匀质摆杆所受转轴约束力分析

肖长江，王晓磊，魏 勇

（燕山大学里仁学院，河北秦皇岛 066004）

分析重力场中匀质杆绕固定轴的摆动过程，给出轴对杆约束力的大小和方向随杆摆角和摆长变化的定量关系，利用Matlab分析了约束力的变化特点，更加直观形象地阐释了其变力属性。

Matlab；匀质杆；转动惯量；力矩；约束力

匀质杆的摆动问题是物理学中的典型问题，摆动过程中其约束力的大小和方向是不断变化的，找出约束力变化的规律及影响因素对于明确其变力属性有很重要的实际意义，对物理教学也有一定参考意义。为便于分析，对约束力和摆长进行了无量纲化处理。

1 匀质摆杆所受约束力的理论分析

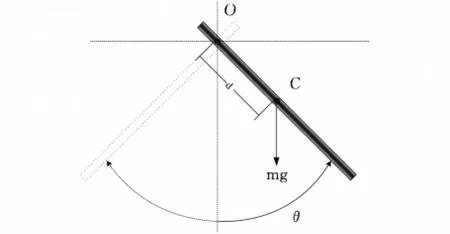
图1 匀质杆的定轴摆动

对O轴而言，杆所受合力矩为重力力矩，即，

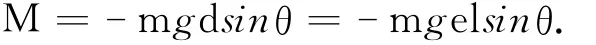
设杆处于水平位置时，角速度为0，进一步，由角加速度的定义

分离变量，并积分得

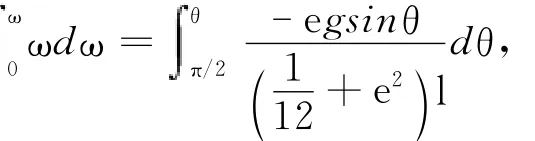
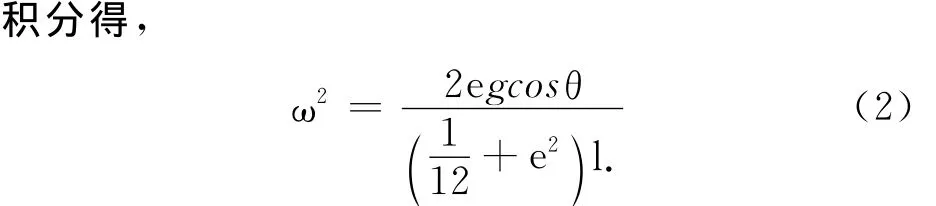
由公式（1）和公式（2）可得，质心的切向加速度和法向加速度分别为

故，质心总加速度的大小为

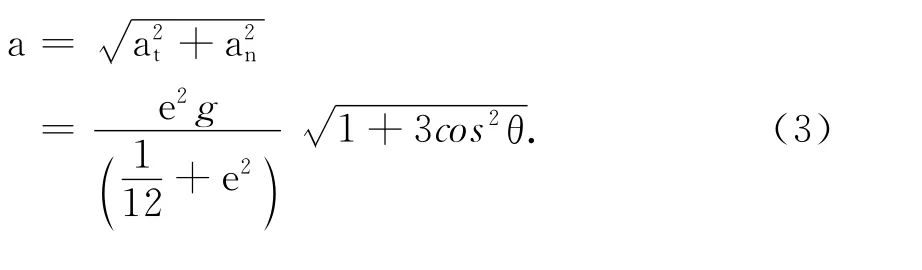
方向用总加速度与切向的夹角θ表示

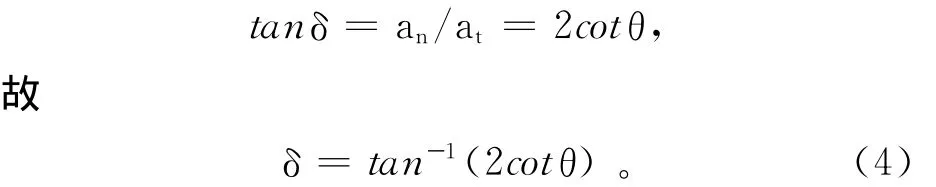
对杆而言，所受外力为重力和轴对杆的约束力，由质心运动定理［1－2］可知m g＋N＝ma，如图2所示，三个力构成一个三角形，利用余弦定理可得

将公式（3）和（4）代入上式得，支持力的大小随θ角和e的变化关系如下式所示：

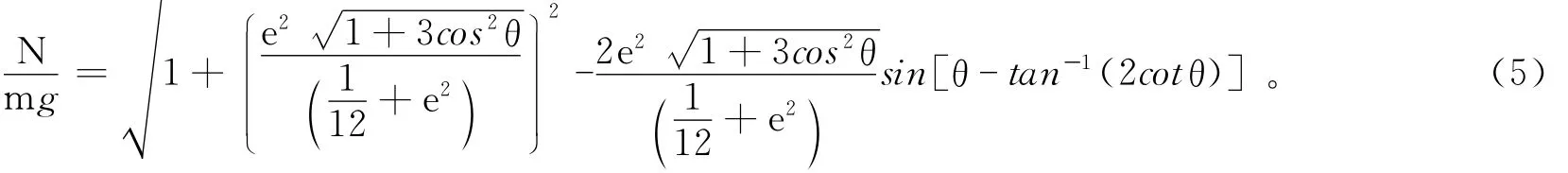
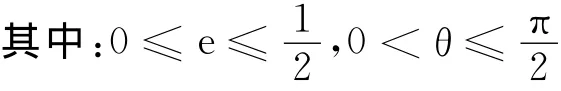
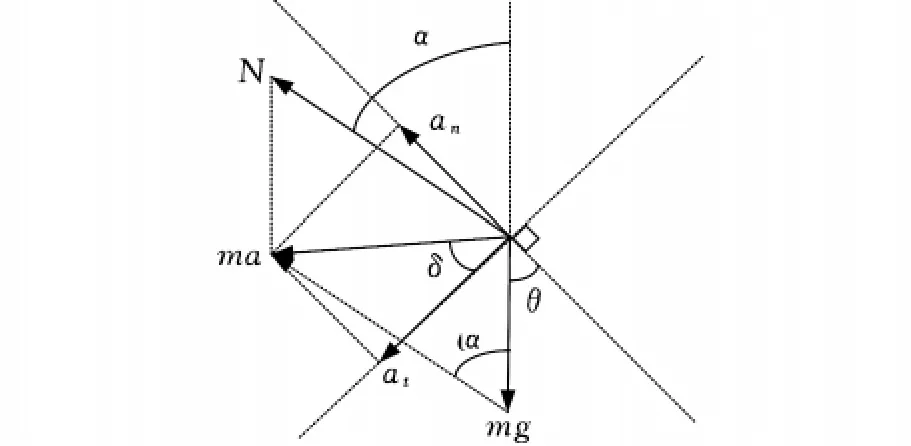
图2 对匀质杆整体的受力分析

关于支持力的方向可以用支持力与竖直方向的夹角α表示，由正弦定理得，

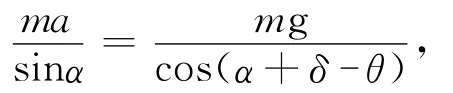
将公式（3）代入得

将公式（4）代入上式，可得支持力方向随θ角和e的变化关系

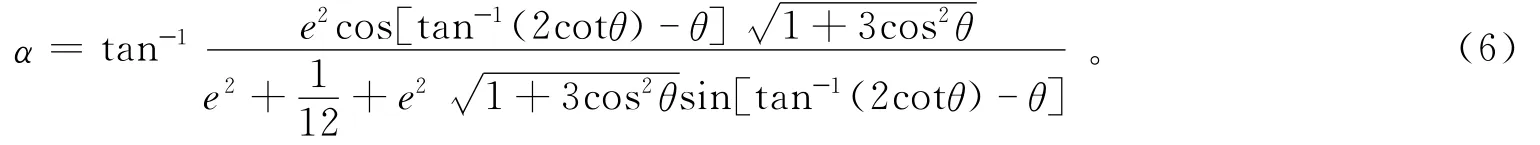
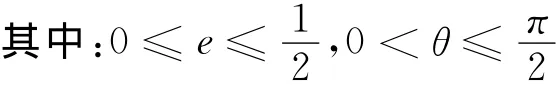
2 对约束力的数值模拟结果

利用Matlab对公式（5）进行分析，得出约束力大小随摆角和摆长的变化曲线，如图3所示，由图可知除摆长e＝0情况外，随摆角增大，摆杆所受约束力在非线性减小，且当摆角约在0～1 rad范围内时，无论摆长怎么变化，约束力始终大于重力；当摆角约在1.2 rad以上时，无论摆长怎么变化，约束力始终小于重力；当摆角约在1～1.2 rad之间时，摆长的变化亦会影响到约束力的变化。当摆长e＝0时，无论摆角如何变化，约束力不变，并且始终等于重力。

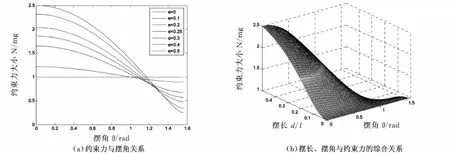
图3 约束力随摆角和摆长的变化

利用Matlab对公式（6）分析，如图4所示，约束力的方向角随摆角的增大先增大后减小，中间存在一个极值，且除e＝0的情况外，随相对摆长e的增大，该极值也在增大。

对于θ角为负值的情况，由于摆动的对称性，故只需将角度变换一下符号即可，这里不再赘述，以上分析说明摆杆所受约束力的大小和方向不仅与摆角有关还与摆长有关，因此摆杆的约束力有其复杂性。

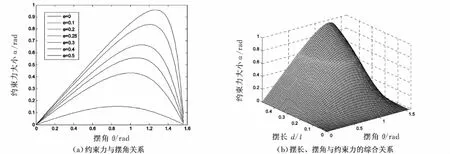
图4 约束力方向角随摆角和摆长的变化

3 结 语

基于刚体定轴转动定律和质心运动定理，得出匀质杆所受轴的约束力的大小与方向和杆的摆角与摆长之间的定量关系，利用Matlab给出了数值模拟结果，并对结果进行了分析，这对于任意转动刚体所受轴的约束力的分析具有一定借鉴意义，同时有助于加深学生对摆动物体所受约束力的变力属性的认识。

［1］ 卢德馨.大学物理学［M］.北京：高等教育出版社，2003.

［2］ 宋伟等.大学物理［M］.北京：国防工业出版社，2009.

Analysis of the Constraint Force of the Spindle in Uniform Mass Distribution Rod of Fixed Axis Based on Matlab

XIAO Chang－jiang，WANG Xiao-lei，WEI Yong

（Liren College，Yanshan University，Hebei Qinhuangdao 066004）

The constraint force of the spindle in uniform mass distribution rod of fixed axis rotation is analysed in gravity field，and the quantified relationship between the magnitude and direction of constraint force and the oscillation angle and oscillation length is given.The relationship graph between them is given by Matlab.It is visual for the cognition of the variable force nature of the constraint.

Matlab；uniform mass distribution rod；inertia；torque；constraint force

O 301

A

1007-2934（2011）05-0073-03

2011-06-07