输油管线布置的最优设计

吕良军，张 兵

（黄河水利职业技术学院，河南 开封 475001）

0 引言

某油田计划在铁路线一侧建造两家炼油厂，同时在铁路线上增建一个车站，用来运送成品油，并且要使管线建设费用最省。 设计方案要做到在两炼油厂到铁路线距离与两厂间距离不同的条件下，尽量使管线建设费用最省。 在进行方案设计时，若两厂在输油点到车站间有共用管线，还要考虑共用管线费用与非共用管线费用相同或不同的情形。

1 问题的分析

由于两炼油厂到铁路线距离和两炼油厂之间的距离都不确定，各种不同情形都必须要考虑。 经分析讨论，得出了两炼油厂位置可能存在以下5 种情形（如图1 所示）。

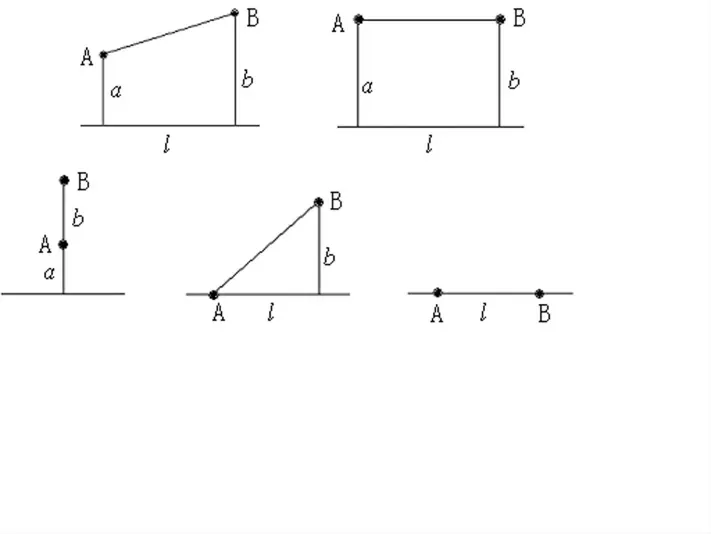
图1 两炼油厂位置的各种情形Fig.1 Various cases of two refineries’ location

显然，第1 种具有代表性，只要改变a、b、l 的参数值，就可以得到后几种情形。 对于共用管线费用与非共用管线费用相同或不同的情形，可设每千米的非共用管道费用设为m 万元，每千米共用管道费用为km(1≤k≤2)万元，当k=1 时费用相同。

2 模型建立与求解

非线性规划的模型[1]一般可写为：

其中X=(x1,x2, ……,xn)T表示n 维向量X∈D，D称为可行域。 把满足条件的解称为可行解，所有可行解的集合即为可行域D，简记为minf(X)。 非线性规划问题的最优解，从广义上说，也是约束条件下的极值问题。

对于多变量函数，在数学分析中求极值的法则z=f(x1，x2，,……，xn)中，求已给域上的极值点和极值，必须使偏导数等于零，即fxi'=(x1，x2，……，xn)=0(i=1，2，…，n)。

图2 两炼油厂位置的一般情形Fig.2 General cases of two refineries’ location

现以铁路线所在的直线为x 轴，A 厂到车站的垂线所在的直线为y 轴，O 点为坐标原点，建立平面直角坐标系（如图2 所示）。 设两厂所铺设的管线的交点E 的坐标为E (x,y), 厂距离铁路的垂直距离为a， B 厂距离铁路的垂直距离为b，OC=1，则A、B 两点的坐标分别为A(0，a),B(l,b)每千米的非共用管道费用设为m 万元， 每千米共用管道费用设为km 万元。 则建立管线建设费用最省的数学模型如式（2）所示：

设m=1，分别对x，y 求偏导函数得：

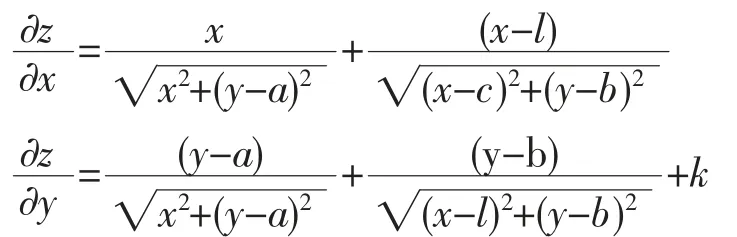
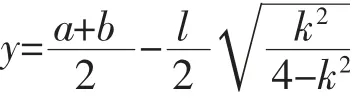
下面对两炼油厂到铁路距离与两厂间距离不同情况进行讨论，不妨假设a≤b。

图3 不同情形下的管线路径Fig.3 Pipeline routes under different situations

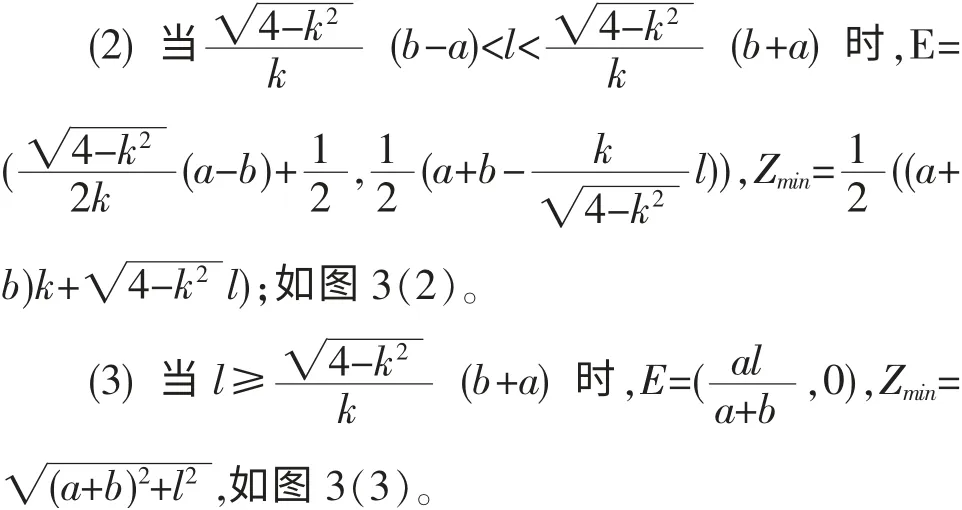
对共用管道费用与非共用管道费用相同的情形，只需在上式中令k=1 即可。

3 实例应用

现有两炼油厂的具体位置如图4 所示。 需要根据炼油厂的生产能力，选用相适应的油管。 管线铺设费用将分别为输送A 厂成品油的每千米5.6 万元，输送B 厂成品油的每千米6.0 万元，共用管线费用为每千米7.2 万元。 铺设在城区的管线还需增加拆迁和工程补偿等附加费用。 为对此项附加费用进行估计，聘请3 家工程咨询公司（其中公司1 具有甲级资质，公司2 和公司3 具有乙级资质）进行了估算。 估算结果如表1 所示：

表1 工程附加费用估算Table 1 Engineering extracharge estimation

请给出管线最佳布置方案及相应的费用。

图4 两炼油厂的具体位置Fig.4 Two refineries’ location

3.1 附加费用的估算

在对该附加费用进行估算时，由于聘请的工程咨询公司存在资质的不同，为更好地计算出结果，首先需要对3 家公司附加费用的数据进行处理。

通过表1， 引入3 家公司资质及附加费用两个因素对基建的影响程度的大小的比值，得到一个对比矩阵[2]如下：

其中R（1，2）=3，即表示公司1 资质及附加费用两个因素对基建的影响程度与公司2 的比值为3，R(2，3)=1，即表示公司2 资质及附加费用两个因素对基建的影响程度与公司3 的比值为1。 利用MATLAB， 求出对比矩阵R 的最大特征根λ=2.8017， 对 应 的 特 征 向 量n 为(0.9045,0.3015,0.3015)，归一化后，为（0.6，0.2，0.2）。 该结果是3 家公司对基建影响分别所占的权重，得出处理后估算的附加费用值

3.2 建立模型及求解

图5 坐标系中的两炼油厂位置Fig.5 Two refineries’ location in coordinate system

建立如图5 所示的坐标系，点H 为城郊分界线与管线的交点。 建立的数学模型为：minz=5.6×。分别对x1,y1,y2求偏导数，并令。 用matlab[3]解此方程组，得x1=6.7337,y1=0.1389,y2=7.2796。 代入目标函数得：Zmin=251.9685。

3.3 模型检验

用优化软件LINGO[4]在区域范围内搜索检验，程序如下：

min=(((5-y1)^2+x1^2)^(1/2))*5.6+(((15-x1)^2+(y2-y1)^2)^(1/2)+(25+(8-y2)^2)^(1/2))*6+y1*7.2+(25+(8-y2)^2)^(1/2)*21.4。

运行结果为：z=251.4633,X1=6.735476,Y1=0.1376764,Y2=7.276816. 其结果与本文所建立的模型计算结果基本相一致。

4 结语

本文全面讨论各种条件下的管线布置的优化问题，并建立起与之相对应的数学模型。 运用相应的数学软件和方法，得出最优解，选择出最佳输油管的设计方案，并计算出建设管线的最省费用。 采用实际例子加以讨论、分析和检验，以期使之更具有实用和推广价值。

[1] 赵静，但琦. 数学建模与数学实验[M]. 3 版. 北京：高等教育出版社，2007：90-91.

[2] 姜启源，谢金星. 数学建模案例选集[M]. 北京：高等教育出版社，2007：169-172.

[3] 肖华勇. 基于MATLAB 和LINGO 的数学实验[M]. 西安：西北工业大学出版社，2008：2-5.

[4] 谢金星， 薛毅. 优化建模与LINDO/LINGO 软件[M]. 北京：清华大学出版社，2005：86-88.