一种求解货物配送问题的改进算法

包得海，管会生

（1．甘肃民族师范学院计算机与科学系，中国合作 747000;2．兰州大学信息科学与工程学院，中国兰州 730000）

一种求解货物配送问题的改进算法

包得海1，管会生2*

（1．甘肃民族师范学院计算机与科学系，中国合作 747000;2．兰州大学信息科学与工程学院，中国兰州 730000）

针对货物配送问题，建立问题的数学模型，提出一种基于禁忌搜索的蚁群算法．并结合超市配送问题，对算法进行测试，测试结果表明，该算法具有收敛速度快、不易陷入局部最优、求解精度高的特点，能够有效地解决超市配送问题．

超市配送问题;蚁群算法;车辆路径问题;禁忌搜索;局部搜索

传统的货物配送问题是在假定先送货后取货的情况下建立的数学模型，这与现时代的实际问题并不相符．本文以超市配送问题为例，如有些超市同时具有送货及取货的需求，又如，从一些超市取出的货物可以配送到另一些超市中．本研究针对传统的超市配送问题加以修改，允许先取货后送货，并把每个超市都设为具有送货、取货或者二者兼有，并允许货物被重复利用．

由于超市配送问题属于车辆运输问题，所以超市配送问题属于NP-hard问题［1］，当配送的超市点很多时，若仍使用传统的数学模型求解，其求解时间将呈指数级别增长．因此，本文构建新的超市配送问题的数学模型，并提出一种以蚁群算法为基础并加入禁忌搜法思想的改进蚁群算法．

在过去国内外学者相关研究中Clark-Wright［2］提出节省法研究车辆途程问题;Deif和Bodin［3］在文献［2］的基础上，加入奖惩值的观念;Goetschalckk和Jacobs-Blech［4］提出两阶段的启发算法;otvin及Laporte［5］使用基因演化算法来求解．文献［6］和［7］分别使用简单近邻法来研究可变速的车辆路径问题和一般车辆路径问题;文献［8］在文献［2］的基础上加入可变速的思想;文献［9］将禁忌搜索方法应用到带时间窗口的可变速车辆路径中．文献［10］利用禁忌搜索算法分两阶段来研究时变速车辆运输问题．上述文献都假设要先送货后取货，且没有考虑可对同一需求点同时做取货与送货的服务，这与实际情况不相符．

蚁群算法是M．Dorigo等人最早提出的，该算法是从蚁群觅食过程中得到启发而构造出的一种算法，但该算法具有易于过早收敛于局部最优解的缺陷．为了改善上述缺陷，本文算法将禁忌搜索思想引入到蚁群算法中，构造出一种新的算法，并把该算法运用到超市配送问题中，以国际算例为例，进行测试，实验结果表明，该算法具有收敛速度快、不易陷入局部最优、求解精度高的特点，能够有效地解决超市配送问题．

1 数学模型

本文数学模型的建立考虑的参数及模型如下:

在该类问题中，V为所有结点的集合，V={i}，i=0，1，2，…，n，i=0表示配送中心，i=1，2，3，…，n为超市需求点;I表示所有超市需求点集合，I={i}，i=1，2，…，n，V=I∨{0}，0表示配送中心;M表示所有车辆的集合，M={k}，k=1，2，…，m;Q表示车辆的最大载重量，本文中假定所有车辆的载重量相同;Cij表示两超市i与j之间的距离，其中，Cii=∞，C00=0，i∈V，j∈V;Pi表示超市的取货量，i∈I;di表示超市i的送货量，i∈I;tij表示超市i至超市j的旅行时间，i∈I，j∈I;tik表示车辆k离开超市i的时间，i∈I，k∈M; Sik表示车辆k在超市i的服务时间，i∈I，k∈M;Pijk表示从超市i到达超市j时车辆k上的送货量，其中i，j∈I，k∈M;Dijk表示从超市i到达超市j时车辆k的取货量，其中，i，j，k∈I，k∈M．

定义决策变量:

数学模型可表示为

其中，式（1）和（2）为目标函数，其目标使总运送成本最小;式（3）保证每个超市被服务一次且仅为一次，且仅有一辆车服务;式（4）至式（7）保证车辆任何时间所载货物不能超过其最大能力，式（4）中P0jk表示从配送中心到达超市j时车辆k上的送货量;式（8）保证车辆出发前收集需求为零;式（9）保证回到配送中心时送货需求为零;式（10）和（11）保证离开配送中心的车辆数等于回到配送中心的车辆数;式（12）表示车辆在超市间行驶时间与与离开某超市和该超市服务时间的关系;式（13）表示相邻结点组成的路段集;式（14）表示所有结点的可行路线组成的链路集．

2 算法描述

本算法使用基于禁忌搜索的蚁群算法求得初始解，在此基础上，进行了第二阶段的优化，采用移步法加以优化．

2．1 初始解生成

具体步骤如下:

①设定各参数的值．蚂蚁的个数为s，最大进化代数为tmax=2 000，当前进化代数t=0，信息素τ=1，禁忌表TSB全部置0．

②将s只蚂蚁随机放置于n个超市上，第w只蚂蚁在t时刻在超市i选择运动到超市j的概率为:

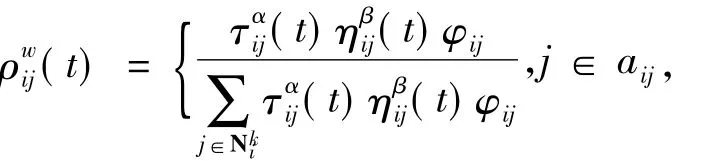
式中aij是第w只蚂蚁可选的与超市i相连的超市集合，τij（t）表t时刻边（i，j）上的信息素浓度;ηij（t）是一个启发式因子，表示在t时刻蚂蚁从超市i转移到超市j的期望程度，在本算法中取ηij（t）=Dijk;α和β分别表示路径上信息量和启发式因子的重要程度，对于每个边（i，j），r是常数，λij（t）代表边（i，j）的使用频率，λij（0）=1，每当边（i，j）被走过一次后λij（t）就增加1．

③每只蚂蚁在构造解的路径时，对蚂蚁走过的路径的信息素浓度采用局部更新规则来更新相应路段上的信息素浓度，更新规则为:

式中ρ表示遗忘因子;τij（t）表t时刻边（i，j）上的信息素浓度;τij（t+1）表t+1时刻边（i，j）上的信息素浓度;

式中τ为开始设置的每条边上的信息素浓度，是个常数，本算法中τ=1，cij表示（i，j）之间的距离．

④当每只蚂蚁都构造完成各自的解之后，记录当前最优化路径，并对最优化路径上的边信息素再次更新，更新公式为:

式中lmin表示当前最短路径，τ'为更新前最优路径上信息素浓度．

⑤禁忌搜索:若当前最优解ri=xk（i=1，2，…，n），则修改禁忌表，将禁忌表中对应的元素置1，否则执行禁忌搜索算法中的特赦规则，将禁忌路段中那些使用率较低或几个路段使用率相同时，优先解禁最短者，将禁忌表相应位置置0，重复步骤⑤，其中使用率由下式决定:

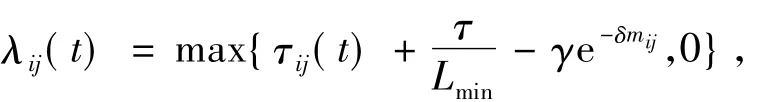
其中τij（t）表示t时刻路段（i，j）上的信息素浓度;γ，δ为设计参数，表示路段使用次数的影响因子;mij表示路段（i，j）总的使用次数;lmin表示当前最短路径;τ为当前路径上信息素浓度．

⑥若满足输出条件（如达到最大进化代数tmax=2 000），则输出最优解，否则t=t+1，转②．

⑦依式Savc（i，j）=2c0c－（cic+cjc－cij）（其中i，j两点为⑥中最优解中的送货超市点，c点为欲插入最优解中的取货超市点，cij为i，j两点间的距离），计算出插入节省值大小顺序，将取货超市点插入距离送货路段中最近的路段．

⑧判断是否超出容量限制，若是，转步骤⑨，否则返回步骤⑦．

⑨节省值次大者，将取货点插入到符合其他路段中，依次类推，若所有取货点都已经插入各路段中，则结束程序，否则转⑦．

2．2 改善初始解

建立初始解阶段获得的解为起始解，利用各种移步法则可以求得更佳的区域解．

本阶段主要对刚取得的初始解，依次运用2-Exchange、2-Swap、2-opt及插入法4种移步法加以改善．

4种移步法则分别说明如下:

（1）2-Exchange

设路经0-1-2-3-4-5-0和0-6-7-8-9-10-0为选取的两条不同路线，0表示配送点，在这两条路线中各选择一段路线，如分别为（2，3）和（7，8），将此两段路线删除，另外增加两段路线（2，8）和（7，3），则可得到两条新的路线0-1-2-8-9-10-0和0-6-7-3-4-5-0．

（2）2-Swap

设路经0-1-2-3-4-5-0和0-6-7-8-9-10-0为选取的两条不同路线，0表示配送点，在这两条路线中各选择一个节点，如分别为2和7，将此两节点互换，则可得到两条新的路线0-1-7-3-4-5-0和0-6-2-8-9-10-0

（3）2-opt

设路经0-1-2-3-4-5-6-0，0表示配送点，在这条路线中删除（2，3）和（4，5）两段路线，再增加两段路线（2，4）和（5，3），则可得到一条新的路线0-1-2-4-3-5-6-0

（4）插入法

设路经0-1-2-3-4-5-0和0-6-7-8-9-10-0为选取的两条不同路线，0表示配送点，在这两条路线中选择一个节点和一段路线，如分别为2和（7，8），将节点2插入到路线（7，8）内，则可得到两条新的路线0-1-3-4-5-0和0-6-7-2-8-9-10-0通过上述4种移步法则，对初始解路经进行了改善．

3 试验结果

为了测试算法的有效性，本文共对已知的15个国际算例进行测试，并与目前已知的最好结果进行了比较，测试结果如表1，测试中的参数取值分别为:α=4．0，β=1．0，ρ=0．9，τ=1，τ'=0．05，γ=1．

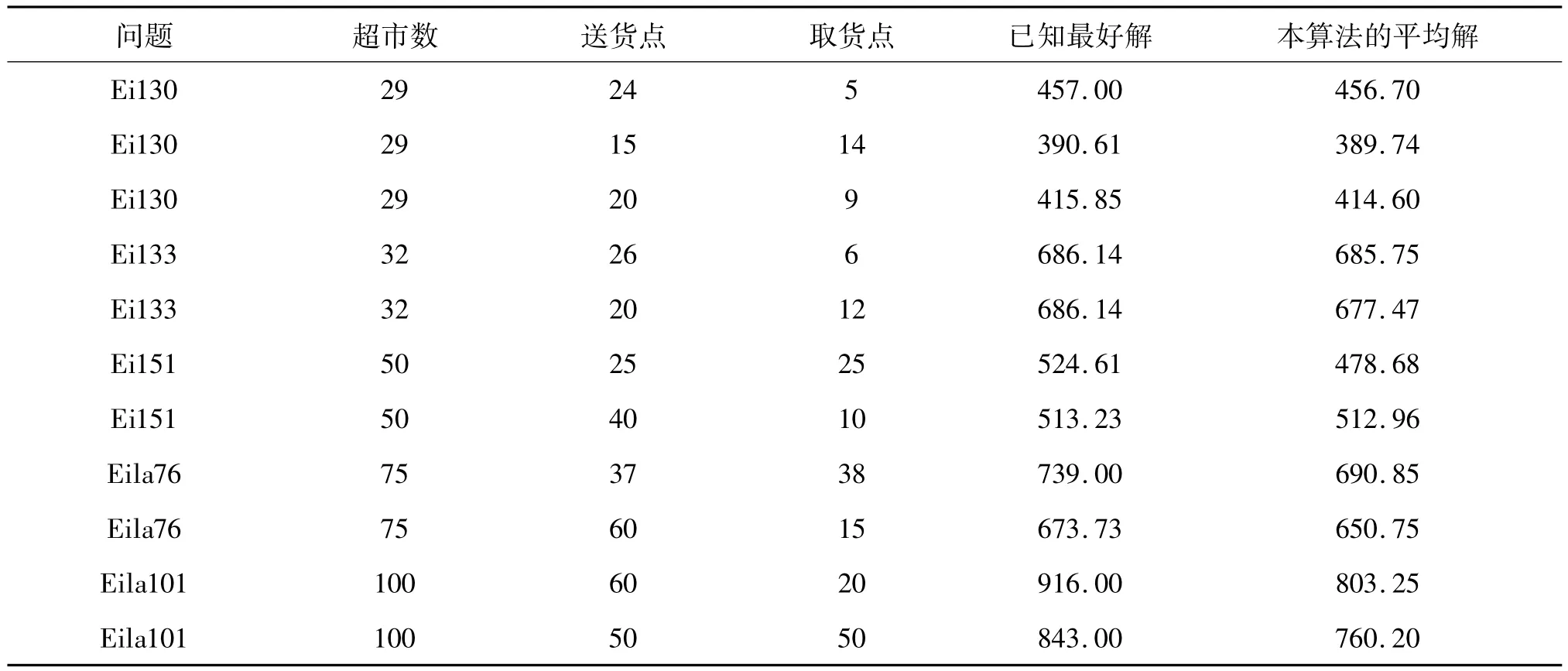
表1 本文算法测试结果与文献结果比较

由表1测试的结果显示，本文所提算法均可得到最佳解，对小规模问题的求解与现有文献的最优解相差无几，但随着问题规模增大，本文所提算法优势明显．

4 小结

本文将禁忌搜索思想引入到蚁群算法中，提出一种改进算法，并与国际算例相结合，加以验证．仿真结果表明，该算法在保证收敛速度的同时，大大提高了解的质量，对于不同规模的问题，算法性能良好．

［1］REINGOLD E M，NEIVERGELT J，DEO N．Combinatorial algorithms:theory and practice prentice-hall［M］．New Jersey: Prentice-Hall，1977．

［2］CLARKE G，WRIGHT J W．Scheduling of vehicles from a central depot to a number of delivery points［J］．Oper Res，1964，12 （4）:568-581．

［3］DEIF I，BODIN L．Extensoin of the clarke and wright algorithm for solving the vehicle routing problem with backhauling:Proceedings of the Babson Conference on software in Trandportation and Logistic Management，Babson Park，MA，1984［C］．MA: Babson Park，1984．

［4］GOETSCHALCKX M，JACOBS-BLECHA C．The vehicle routing problem with backhauling［J］．Eur J Oper Res，1989，42（1）: 39-51．

［5］POTVIN J Y，LAPORTE G．Genetic algorithm for the traveling salesman problem［J］．Ann Operat Res，1996，63:339-370．

［6］HILL A C，BENTON W C．Modeling intra-city time-dependent travel speeds for vehicle scheduling problems［J］．J Oper Res Soc，1992，43（4）:343-351．

［7］MALANDRAKI C，DASKIN M S．Time dependent vehicle routing problems:formulation，properties and heuristic algorithms［J］．Trans Sci，1992，26（3）:185-200．

［8］PARK R B，Song S H．Vehicle scheduling problems with time-varying speed［J］．Comput Ind Eng，1997，33（3-4）:853-856．

［9］ICHOUA S，GENDREAU M，POTVIN J Y．Vehicle dispatching with time-dependent travel times［J］．Eur J Oper Res，2003，144（2）:379-396．

［10］DUHAMEL C，POTVINN J Y，ROUSSEAU J M．A tabu search heuristic for the vehicle routing problem with backhauls and time windows［J］．Trans Sci，1997，31（1）:49-59．

［11］DORIGO M，MANIEZZO V，COLORNI A．The ant system:optimization by a colony of cooperating agents［J］．IEEE Trans SMC，Part B，1996，26（1）:29-41．

An Improved Algorithm of Solving Goods Distribution Problem

BAO De-hai1，GUAN Hui-sheng2*
（1．Department of Computer Science，Gansu Normal University for Nationalities，Hezuo 747000，China; 2．School of Information Science and Engineering，Lanzhou University，Lanzhou 730000，China）

A mathematical model for Goods Distribution Problem is constructed and an ant colony algorithm with tabu search is put forward．The algorithm is tested in combination with Supermarket Distribution Problem．The experimental results indicate that the algorithm solves Supermarket Distribution Problem effectively with quick convergence，avoid local optimum，high precision solution characteristics．

supermarket distribution problem;ant colony algorithm;VRP;tabu search;local search

TP301．6

A

1000-2537（2011）05-0012-05

2010-11-16

甘肃省教育厅科研基金资助项目（1012-06）

*通讯作者，E-mail:hzmtcb@126．com

（编辑沈小玲）