电磁主动防护系统中拦截效果的仿真计算分析*

孙 鹏,雷 彬,李治源,史忠鹏

(解放军军械工程学院,石家庄 050003)

0 引言

现有的车载主动防护系统都是通过火药燃烧产生的化学能作用进行发射,对速度在1～2个音速之间的反装甲导弹,留给系统的反应时间相对较长,但对于最大速度可达1700m/s以上的高速脱壳穿甲弹,从弹丸进入有效拦截范围内到接触装甲表面仅有几毫秒。而在如此短的时间内,不论是美国的“密集阵”、荷兰的“守门员”还是我国的“730”近程反导系统,其最高射速也只有6000发/min,极大的限制了对高速目标的拦截效果。而电磁主动防护系统的射速理论上可达60000发/min,发射系统的反应时间为亚毫秒级,这样可以对来袭目标进行有效拦截。

文中以电磁发射原理为基础,根据近程防护武器末端拦截命中概率算法,结合电磁发射的特点,给出电磁发射主动防护系统拦截概率的模型,通过Matlab软件对模型进行仿真和计算,应用LS-DYNA软件模拟拦截板对来袭目标的拦截效果,确定有效拦截弹丸数,并分析了影响电磁发射拦截概率的几种参数配置,为进一步探索装甲车辆的新型主动防护方式打下良好的理论基础。

1 电磁主动防护系统

1.1 电磁发射原理

电磁发射原理如图1所示,开关闭合时,储能电容器对驱动线圈放电并在其周围产生脉冲磁场,该轴向磁场B的变化在非导磁性材料拦截板上产生涡流,涡流与驱动线圈产生的径向磁场B′相互作用,使拦截板受反向安培力的作用发射出去[1]。

1.2 电磁主动防护系统的组成

主动防护系统包括探测系统、火控系统、脉冲电源和控制系统、拦截板等多个系统组成,如图1所示。电磁发射有射速高、可实现模块化结构等特点,主要性能均优于化学发射[2]。在拦截板发射瞬间系统的工作过程为:当探测系统发现和识别高速来袭目标时,控制系统向拦截装置发出触发信号,触发信号将拦截装置的开关闭合,储能电容器通过开关、脉冲成形网络和发射线圈放电,形成脉冲强磁场,拦截板受到电磁力的作用被发射出去撞击来袭目标,使来袭射弹被摧毁或者末段弹道性能受到严重影响,从而减小主装甲所受到的破坏。电磁主动防护系统的工作过程如图2所示。

图1 拦截板电磁发射原理图

图2 电磁主动防护系统的工作过程

2 电磁主动拦截系统的数学模型

2.1 Z坐标系的建立

建立空间Z坐标系如图3所示(为右手系),坐标原点与预测拦截点Tq重合;z1轴在水平面上,并指向提前点水平距离d q方向;z2轴垂直于水平面,并指向高度方向;z3轴垂直于z1 z2平面(即提前拦截发射面),并指向目标航路一侧。

图3 Z坐标系

电磁主动防护系统对装甲车辆进行防护时,拦截区域可认为是以装甲车中心为圆心,半径为R的半圆球,如图4所示。拦截区有效半径为30m,拦截板是20cm×30cm的长方形铝板,可将多具拦截板发射器呈一定角度排列(如三具一组,互成 60°排列)。因此拦截器可以覆盖于装甲车辆表面,只要探测系统和火控系统精度足够高,对来袭目标运动参数判断准确,就可以最大程度的减小拦截死区。

图4 拦截板拦截范围示意图

2.2 来袭目标运动参数的计算

设来袭目标是匀速直线运动,呈下降趋势,则可根据所给条件确定出预测拦截点为:

式中:t为电磁主动防护系统在预测拦截点进行拦截时来袭目标运动的时间,也就是系统反应的时间;S为运动距离;D和D q为目标斜距离;εq为目标高低角;β为目标方位角;d q为目标水平距离。则在t系统反应时间内发射的拦截弹丸数为:

式中u为电磁主动防护系统射速。

2.3 误差分类和简化

电磁主动防护系统在拦截方式上属于末端拦截,而且为了简化模型,在实际建模过程中考虑的误差有:

1)拦截板高低、方向散布误差 Δy 0、Δz 0为不相关、非重复误差;

2)初速偏差误差引起的射角误差和飞行时间误差 ΔθV0、Δt V0,弹道风误差引起的横风误差 ΔW z和纵风误差ΔW d均属于强相关、重复误差;

3)火控系统误差引起的射角误差 Δφs和提前方位角误差Δβs为弱相关、重复误差;

4)触发控制系统误差引起的高低瞄准误差 Δφm和方向瞄准误差Δβm为不相关误差。

通过上面对拦截误差的分析,可将电磁主动防护系统的误差源在预测拦截点引起的误差均方差,在Z坐标系中按方向总结为下面三种误差均方差:

σ1:在射面内,垂直于斜距D q的误差,有 Δσn0、Δσφm、ΔσθV0、Δσθw、Δσφs、Δσmφs;

σ2:与目标航路方向相同的误差,有 ΔσtV0、Δσtw;

σ3:与射面垂直的误差 ,有 Δσz0、Δσβm 、ΔσWz、Δσβs、

由各个误差组成的协方差阵为三类误差。为便于计算,将三类误差转换为二类误差。为了使弱相关误差能够符合射击效率,计算中按误差重复性分组原则,需要对其进行近似处理。这里对弱相关误差分为两个部分:不相关误差和强相关误差,由于这两部分是不相关的,则有:

式中:σrb为弱相关误差中的不相关部分的均方差;σrg为弱相关误差中的强相关部分的均方差;C r是比重系数,可通过最小二乘法进行求解。

对武器的发射射速为u发/s,射拦截发射时间间隔为Δτ=1/u,则单具拦截器一次发射的时间长度为τ=(n-1)Δτ。则时差为 kΔτ的两次发射有(n-k)种,电磁主动防护系统的探测系统误差的相关系数为e-αkΔτ。经推导[3]有:

则可将三类误差的协方差阵写为:

式中:Kb、Kr和Kg分别为不相关误差协方差阵、弱相关误差协方差阵和强相关误差协方差阵;K f为非重复误差协方差阵;K c为重复误差协方差阵。

3 仿真条件

在设定拦截概率参数之前先对仿真条件做以下假设:

1)由于电磁主动防护系统发射拦截弹道来袭目标的时间非常短,可假设发射拦截弹拦截来袭目标这段时间内电磁主动防护系统的载体是静止的;

2)假设来袭目标在拦截弹飞行时间内作直线运动,这样来袭目标的航路角和拦截弹发射器的高低角是常数;

3)由于拦截弹飞行的时间和距离非常短,可假设拦截弹作直线飞行运动。

在初始值的设置中输入以下初始参数:

①电磁主动防护系统为雷达测距,车载主动防护系统的防护范围为一半球形的空间,则拦截点位置Dq∈(5～30m)的范围内;拦截弹发射初速V0=30～100m/s,拦截弹拦截面积为0.2m×0.3m;②误差计算中 各参 数量为 :σφm=1mil,σβm=1mil,fθV0=0.07,f tV0=0.06,fθw=-0.5,f tw=0,σWz=2.2mil,f wz=0.1,σφs=σβs=9mil,mφs=5mil,mβs=5mil,σV0=0.1V0;③以脱壳穿甲弹为拦截目标,设其最大速度为 V m=1500 ～ 1800m/s,εq=45°,λ=0,q=30°。

4 仿真结果及分析

4.1 有效毁伤来袭目标弹丸数对拦截概率的影响

因为脱壳穿甲弹弹头与杆部较细长,可由拦截弹的初速和拦截器的各种参数确定有效毁伤弹丸数 ω。击毁同一目标所需的平均命中弹丸数 ω的改变对毁歼概率的影响如图5所示。显见,随着ω值的减小,即所需的有效毁伤来袭目标弹丸数减小可以显著的提高电磁主动防护系统的拦截概率。

只要使拦截板保持一定的初始动能,就可以有效的减小ω值,而ω值的大小根据拦截板的重量G通常能粗略的估算出对来袭目标进行有效毁伤所需的弹丸数 ω。文中所用的弹丸是方形铝板,重量为2kg,在发射初速达到40m/s的基础上,通过LS-DYNA软件中的非线性程序分析包对铝板与动能穿甲弹碰撞进行模拟仿真,如图6所示,由显示的效果可以看出,当一枚拦截弹与动能穿甲弹碰撞时,穿甲弹的杆部已呈碎裂态。因此,在拦截概率的仿真分析中有效毁伤的弹丸数ω值取1。

图5 弹丸威力对于毁歼概率的影响

图6 拦截弹与动能穿甲弹碰撞仿真

4.2 来袭目标运动速度对拦截概率的影响

随着来袭目标运动速度V m的改变,将会影响到拦截过程产生的强相关误差以及目标沿弹道方向在空间坐标系上的投影,因而必将引起拦截概率的改变。电磁主动防护系统研制的目的是对高速目标进行拦截,因此对速度相对较低的反坦克导弹和火箭弹也会具有很好的拦截效果,系统和目标参数不变的条件下,来袭目标运动速度V m由120m/s升高到2000m/s,如图7所示。来袭目标运动速度对拦截概率影响较大,随着V m的增大,拦截概率降低。

图7 来袭目标运动速度对拦截概率的影响

4.3 拦截器高低角设置对拦截概率的影响

电磁主动防护系统中拦截器需要呈一定角度置于车辆顶部,由于发射的拦截弹在空中为一平面,则拦截器高低角的设置会影响到拦截弹与来袭目标接触的角度。因此拦截器高低角的设置对拦截概率会有影响。在系统和目标参数不变的条件下,改变拦截器的高低角,从 0°增大到80°,如图 8所示。当高低角在由32.9°到37.6°时发生较大的改变,并在37.6°时拦截概率达到最大88.67%。从整个高低角变化过程来看,εq在0°～32.9°时,拦截概率降低了 7.5%;而 εq在 37.6°～70°时 ,拦截率降低了20.76%。

图8 拦截器高低角设置对拦截概率的影响

4.4 射速对拦截概率的影响

电磁主动防护系统可以通过对电源模块触发时间的控制有效调节射速的大小,理想状态下,单具拦截器射速的大小只与电源模块中功率开关的频率和控制触发电极的脉冲延迟有关。在无延迟状态下,开关频率可达1k Hz,通过改变触发时间就可以调整发射频率,射弹数n也随之改变。

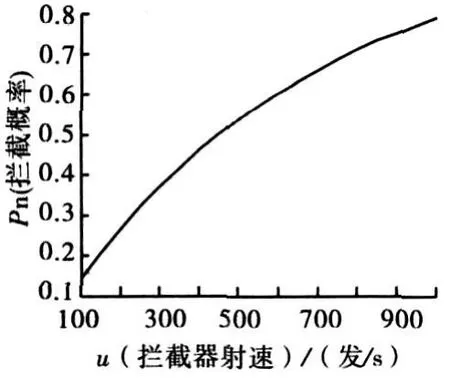
图9 系统射速对拦截概率的影响

从上述因素开关频率可知,实际的拦截过程是在极短时间内完成的。假设其它条件不变,射速u在由100发/s增大到 1000发/s,则拦截概率如图9所示。结果表明,随着射速的增加,拦截概率也随之增加,但增长幅度趋缓,这是因为当达到饱和拦截密度时,增加射弹数n不会持续起到提高拦截概率的效果,而且增大了电源模块的能量消耗。

4.5 来袭目标不同航路角对拦截概率的影响

由所建立的拦截模型可知,航路角q为来袭目标速度矢量与拦截器在水平面上的投影矢量与水平距离的夹角。不同的航路角表示来袭目标方向的不同,当 q在 0°～80°时,即目标对着装

甲车辆接近飞行。分别在 300发/s、600发/s、1000发/s三种射速条件下,对不同航路方向来袭目标的拦截概率如图10所示。可以看出相同参数条件下的航路角,随着射速的升高,拦截概率也在不断增大。由此可见,电磁主动防护系统在超高射速下,对不同航路角的来袭目标均能起到很好的拦截效果。

图10 三种不同射速条件下的拦截概率曲线图

5 结论

文中对电磁主动防护系统拦截过程中出现的误差和对来袭目标的拦截概率进行研究,建立拦截误差模型和拦截概率模型,并对模型进行了仿真和分析,为完成电磁主动防护系统的研制和使用提供技术支持和理论参考。

[1] 胡金锁.电磁装甲技术原理及其有限元分析[M].北京:兵器工业出版社,2005.

[2] Li Zhiyuan,Hu Jinsuo,Wang Ying.Simulating course for plate-ejecting EM armor by single-stage coil gun[C]//11th International Electromagnetic Launch Technology Symposium,Saint-Louis,France,May 14-17,2002.

[3] 田棣华,肖元星,王向威,等.高射武器系统效能分析[M].北京:国防工业出版社,1991.

[4] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2008.

[5] 尚晓江,苏建宇,王化锋,等.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京:中国水利水电出版社,2008.