基于监测数据的桥梁结构可靠性评估

焦美菊，孙利民，李清富

（1.同济大学 土木工程防灾国家重点实验室，上海200092；2.郑州大学 水利水电与环境学院，河南 郑州450002）

近年来，结构健康监测系统（structural health monitoring systems，SHM）在大型桥梁结构中有了较多应用.SHM 能够监测各种不确定性问题，虽然监测数据本身也具有随机性［1］，但是随着数据的积累能够极大地降低不确定性.因此，将SHM 和概率方法相结合，即基于SHM 的桥梁可靠性评估成为桥梁结构性能评估的重要方法.

2006年，Ni Y Q 等［2］提出了基于长期监测数据的桥梁可靠性评估的概念；然而，在其案例分析中并没有利用实际监测数据对桥梁结构进行可靠性评估，而是采用有限元分析模拟监测数据，并将模拟结果用于桥梁构件的可靠性计算.2008 年，Frangopol等［3］在其研究中首次给出了基于SHM 监测数据的桥梁可靠性评估的工程实例应用.同年，Frangopol等［4］提出了基于监测极值的桥梁性能的可靠性评估及预测，并提出了基于贝叶斯更新的桥梁可靠性的预测方法［5］.2009年，Liu Ming 等［6］直接利用SHM监测的桥梁活载效应对桥梁结构进行了安全性评估.随后，Liu Ming等［7］又给出了基于监测数据的桥梁系统的可靠性分析.2010年的最新研究进展有文献［8－9］，另外文献［10－11］对基于SHM 的可靠性研究进行了较为全面的综述.目前，基于SHM 的桥梁结构可靠性评估尚处于研究的初步阶段，且已有的基于SHM 的可靠性研究大都集中在构件的层次，其中文献［7］是基于SHM 的桥梁结构系统层次可靠性评估的为数不多的研究之一.本文的研究是基于构件层次的可靠性评估.

1 可靠性评估

1.1 可靠度基本理论

从安全角度出发，建筑结构等土木基础设施在设计使用年限内，其承载能力必须大于作用于其上的各种荷载所引起的效应，可用下式表示：

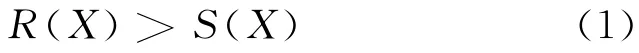
式中：R（X）为结构抗力；S（X）为各种作用在结构上所引起的效应；X为影响结构抗力和效应的各种随机变量.

由此可定义结构的功能函数（又叫安全裕度）为

根据我国《建筑结构可靠度设计统一标准》（以下简称《统一标准》）的定义，结构可靠度指结构在规定的时间内，在规定的条件下完成预定功能的概率.相应地，结构失效概率即为结构不能完成预定功能的概率.结合上述结构的功能函数，由概率统计知识可得到结构的失效概率为

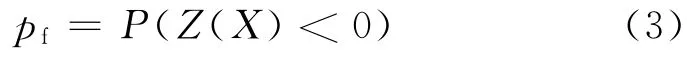
虽然上述关于结构失效概率pf表达式的意义非常明确，但在实际应用中利用式（3）求解结构失效概率往往非常困难.因为影响结构抗力和效应的因素很多，所以利用式（3）求解结构的失效概率往往需要进行多重积分，并且大多数情况下并不存在理论解.为了方便实际工程应用，1969年，Cornell［11］首先提出了“可靠指标”或“安全指标”的概念，并以此作为结构可靠性度量.在国内，根据《统一标准》规定，结构可靠指标与失效概率存在以下关系：

式中：β为结构或构件的可靠指标；Φ－1（·）为标准正态分布函数的反函数.

当式（2）中R和S分别代表结构抗力和效应的综合随机变量，均服从正态分布且相互统计独立时，可靠指标β可由下式计算：

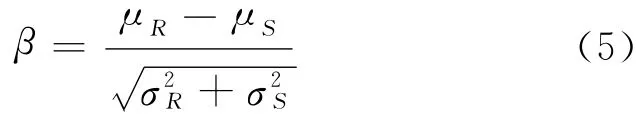
式中：μR和μS分别为抗力和效应的均值分别为抗力和效应的方差.此时失效概率pf和可靠指标β具有一一对应关系.

1.2 验算点法

自20世纪50 年代，国际上开展结构可靠性基本理论的研究起，先后提出的可靠度计算方法有一次二阶矩法、二次二阶矩法、蒙特卡罗（Monte－Carlo）方法及其他方法，其中一次可靠度方法又分为中心点法和验算点法.对于正常使用极限状态等可靠指标较小的情况下，可以采用中心点法，误差不大；对于承载能力极限状态等可靠指标较大的情况，采用中心点法将会带来较大误差［12］.本文拟计算构件屈服强度的可靠指标，因此采用一次可靠度方法的验算点法.

1.2.1 功能函数

东海大桥健康监测系统传感器为成桥后安装，监测结果不包含恒载部分引起的荷载效应，因此对结构功能函数式（2）作以下变化：

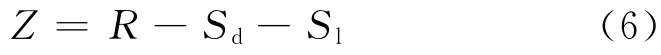
式中：Sd和Sl分别为恒载效应和活载效应.为了后文描述方便，分别用X1，X2和X3表示R，Sd和Sl，用ai（i＝1，2，3）表示Xi的系数.则功能函数可表示为如下的线性形式：

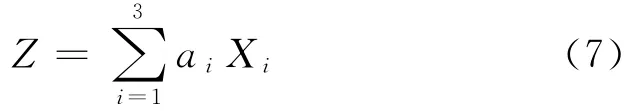
1.2.2 非正态随机变量当量正态化

利用验算点法计算结构或构件的可靠指标时，当功能函数中存在非正态随机变量时，首先需要将非正态随机变量当量正态化.当量正态化必须满足2个条件：在验算点处，使非正态随机变量Xi与当量正态随机变量Xi的概率分布函数相等；使Xi的概率密度函数值与X′i的概率密度函数值相等［12］.根据当量正态化的条件可得当量正态随机变量的均值和标准差为

式中：μX′i和σX′i分别为当量正态化随机变量的均值和标准差为验算点坐标值；Φ（·）和φ（·）分别为标准正态累积分布函数和分布密度函数；FXi（·）和f（·）分别为随机变量Xi累积分布函数和分布密度函数.

在线性功能函数式（7）中，根据文献［13］桥梁结构的恒载效应不拒绝正态分布，活载效应随机变量的分布可以通过监测数据估计，抗力的分布类型未知，在本文计算中假定为正态分布.因此，只需要对活载效应随机变量当量正态化.

1.2.3 可靠指标的计算

对活载效应随机变量当量正态化后，功能函数式（7）中的随机变量均服从正态分布，由式（5）和（7）可得构件的可靠指标为

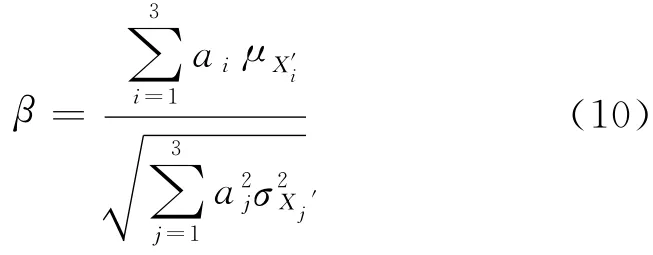
由式（8）—（10）可知，可靠指标β是验算点坐标x＊i的函数，不能直接求解.根据文献［12］，验算点坐标与可靠指标具有以下关系：

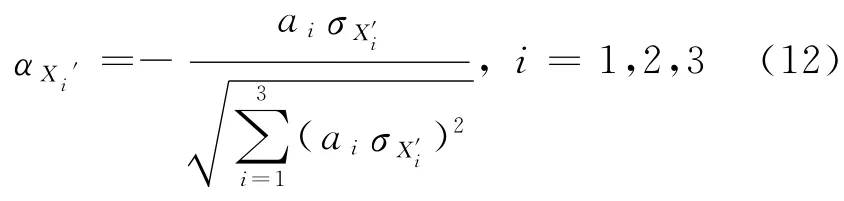
式中式（8）—（12）构成一非线性方程组，可靠指标β和验算点坐标值按以下步骤迭代计算：

③由式（10）计算可靠指标β；

④由式（12）计算αXi′，i＝1，2，3；

2 监测数据的处理

本文主要应用活载应变的监测数据，因此本文所提出的监测数据处理方法是以活载应变为处理对象的.

2.1 已有监测数据的处理方法

目前基于监测数据的桥梁可靠性评估研究中，对监测数据的处理有2 种方式.其一是直接应用，Frangopol等［3］首次利用监测数据进行桥梁可靠性评估时便采用这种方式.随后Frangopol［4－5］又提出了第2种应用方式，即监测极值的应用.在监测极值选取方面又有2种方法，一种是取每天的最大值作为监测极值，这方面的代表性工作主要有文献［7－8］等；另一种是设定一个阈值，其中大于指定阈值的数据便为监测极值，文献［6］便采用这种方式.在已有研究工作中以第2种应用方式居多.

2.2 本文处理方法

2.2.1 东海大桥SHM 简介

东海大桥健康监测系统由实时监测和人工检测2部分组成.实时监测内容包括：气象、结构温度、应变、伸缩缝位移、梁塔振动、索力、梁塔位移和钢结构疲劳等.混凝土桥实时监测内容有：墩台沉降、挠度和结构温度.人工检测包括：冲刷深度、墩台变位、裂缝、混凝土强度、混凝土碳化深度、氯离子侵蚀、钢管桩腐蚀及伸缩缝位移.在实时监测中运用了GPS、光栅光纤等先进的传感技术［14］.全桥有11个采集工作站、478个传感器，其中主航道斜拉桥布设了169个多种类型传感器用于监测结构的响应及环境因素等，详见文献［15］.

2.2.2 应变监测数据特点分析

在结构健康监测系统中应变传感器按照设定的采样频率采集信息.采集到的应变信息包含各种环境因素作用下结构响应和交通荷载作用引起的结构响应.由于应变传感器受温度变化以及传输过程中各种因素的影响，测量信号的随机性由噪声引起.监测信号和真实信号之差为测量误差，文献［9］认为这种误差服从标准正态分布.

本文所采用应变传感器的布置如图1 所示，为东海大桥主航道斜拉桥跨中截面的左侧截面靠分隔带位置，传感器布置在钢混凝土叠合梁的钢底板上.

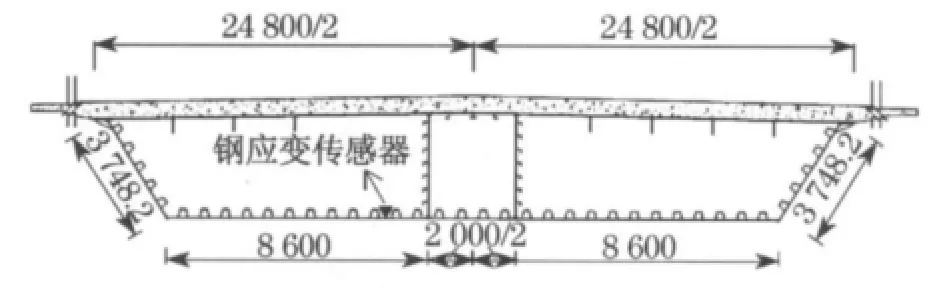
图1 应变传感器布置位置图（单位：mm）Fig.1 Strain sensor location（unit：mm）

图2给出了东海大桥该纵向应变传感器在2007年5月1日下午3点到4点1h的原始信号.为了对信号做进一步分析，图3给出了该信号的功率谱密度（power spectrum density，PSD）.可以看出，信号在低频段f＜0.34Hz信号的PSD随频率的增大而急剧减小；在频率段0.34Hz≤f≤4.50Hz出现多个突出峰值，各峰值点频率如图中所标示；而在高频段f＞4.50 Hz信号的PSD趋于平稳.根据桥梁结构在移动车辆下的强迫振动理论［16］，车辆荷载引起的结构响应可分为移动车辆荷载下的静力响应和车辆振动引起的动力响应.东海大桥设计车速为v＝80km·h－1时车辆引起的广义角频率ω1＝0.166Hz，相应的1 阶频率F1＝0.026Hz，而 东 海 大 桥 的1 阶 竖 弯 频 率f1＝0.366Hz［14］，显然F1≪f1（或Fn≪fn），因此上面应变信号的低频部分由移动车辆荷载引起.由于引起车辆振动的各种激励具有随机性（比如车辆轮周不圆，桥梁的伸缩缝和路面不平等），因此车辆振动频率也是随机的.当采用零均值的高斯随机过程模拟路面平整度［17］时，由路面不平整引起的扰动频率fp＝0.01v～3.0v＝0.222～66.700Hz，和桥梁的各阶竖弯频率相比，车辆振动具备引起共振的条件，因此图3中PSD各峰值点对应桥梁结构的各阶竖弯频率且在频率范围0.34Hz≤f≤4.50Hz的结构响应由车辆的振动引起.在高频阶段，由于信号的PSD趋于平稳，因此这部分信号可认为是由噪声引起.

图2 2007年5月1日15：00至16：00的原始信号Fig.2 Initial strain monitoring data of an hour from 15：00to 16：00on May 1，2007

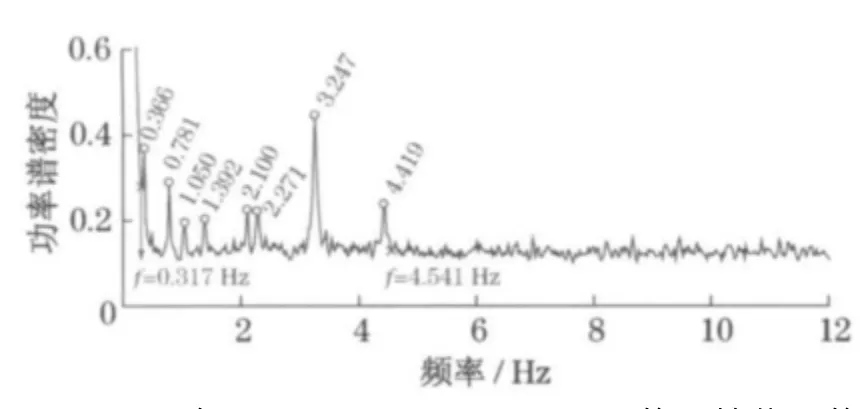
图3 2007年5月1日15：00至16：00的原始信号的PSDFig.3 PSD of the initial strain monitoring data of an hour from 15：00to 16：00on May 1，2007

通过上述分析，本文将原始信号分为3个部分，即平移车辆荷载引起的低频结构响应（或称静态效应），车辆振动引起的动态结构响应和噪声成分.下面针对这3种成分对原始信号进行预处理.

2.2.3 信号的预处理

针对原始信号的上述特点，首先通过低通滤波对原始信号进行去噪处理.从图3 的PSD 图以及上述特点分析，可以看出在f＞4.50 Hz的高频部分，信号的PSD 开始趋于平坦，因此设置低通滤波的最高频率为4.50 Hz.过滤掉的噪声信号如图4所示.可以看出噪声信号基本上是正负均匀地分布在零值附近，统计噪声信号的均值和标准差分别为0和0.99，与文献［9］的标准正态分布的假设相吻合，其均值和标准差与标准正态分布的微小差别是由于受信号长度的影响，以及工程实际与理论的误差，是正常的.

图4 噪声信号Fig.4 Noise signal

根据信号特点分析，滤波后信号包含平移车辆荷载引起的静态响应和振动车辆荷载引起的动态响应.为了进一步分析车辆荷载对构件可靠指标的影响，作者再次对滤波后的信号进行分离.按照上述特点，将滤波信号分离为高频（0.34～4.50Hz）动态信号和低频（0～0.34Hz）静态信号，分离结果分别如图5和图6所示.表1给出了静态信号下构件可靠指标和未分离低通滤波信号下的可靠指标.结果显示，2种信号下的计算结果相差不大.因此，对于东海大桥，认为平移车辆荷载下结构静态响应对构件的可靠指标起控制作用，而车辆振动荷载引起的动态响应对结构可靠指标的影响可以忽略不计.虽然从理论上说应该采用完整车辆荷载下的结构响应进行可靠性分析，但是由于静态响应处于控制地位，且采用静态响应却能极大地减少结构响应的极值，大大减小需要计算的数据量，节省计算时间.另外，静态信号的评估结果比滤波信号的结果小，结果偏于安全.因此建议采用低频静态响应进行构件可靠指标计算.

综上所述，对信号预处理主要就是低频静态信号的分离，可以采用低通滤波方法，对东海大桥主航道桥来说设置滤波信号的最高通过频率为0.34Hz.

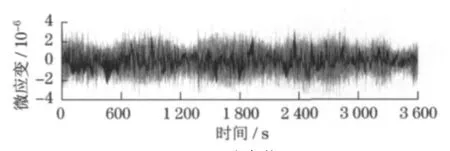
图5 动态信号Fig.5 Dynamic signal

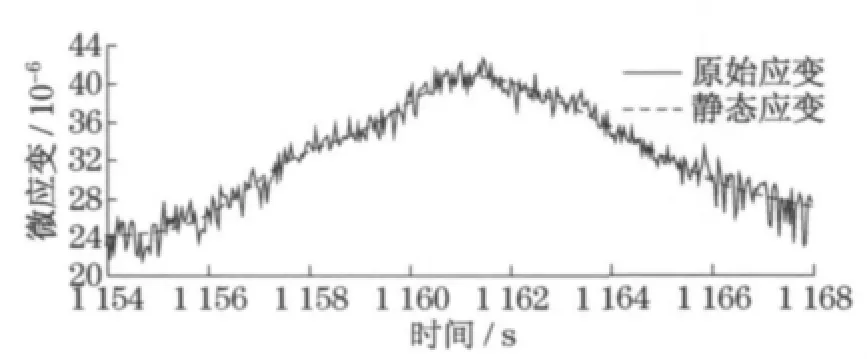
图6 静态信号Fig.6 Static signal

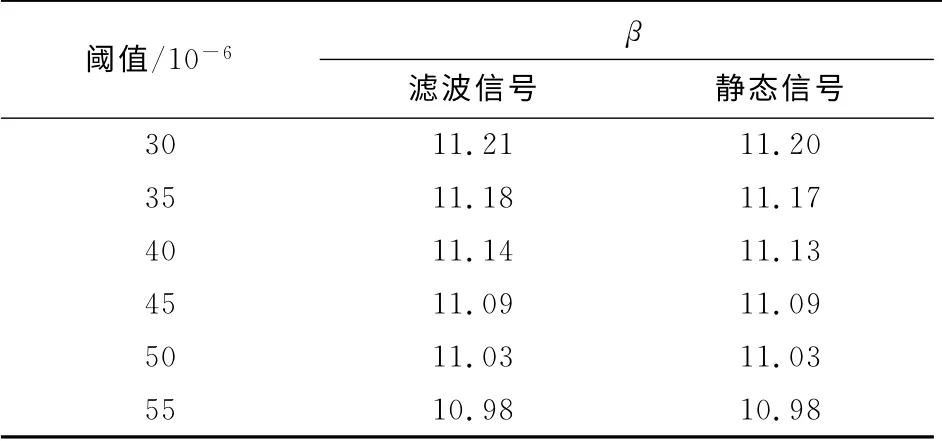
表1 静态信号及滤波信号在不同阈值下的可靠指标Tab.1 Reliability indices of both static and filtering signals with different thresholds

2.2.4 监测极值提取

原始信号经过静态信号分离即可进行监测极大值的提取.首先提取静态信号极大值，相应于直接利用原始信号的方法，极大值提取有效地减少了数据长度.然后设置合适的阈值进行过滤，极大值中大于阈值的部分就是所需要的监测极值.

目前尚未进行阈值大小选择的研究，只是依照经验以及数据量的大小采用.后文简单分析了可靠指标对阈值的敏感性.

3 实例应用

基于上述可靠度评估方法，选择东海大桥主航道斜拉桥主跨跨中截面的应变监测数据，采用验算点法进行跨中截面承载能力极限状态可靠性评估.东海大桥主航道斜拉桥钢箱梁采用Q345qD 钢.该钢材屈服强度为345 MPa.其屈服强度变异因数理论上应该采用评估对象材料试验报告中的材料统计参数.这里因为作者无法得到这份报告，因此采用文献［18］所统计的6 家钢厂24组Q345qD 钢的屈服强度变异因数的平均值0.07，则该钢材的屈服强度平均值为μ＝345÷（1－1.645×0.07）＝390 MPa.式（6）中恒载效应均值通过有限元分析计算确定，恒载效应变异因数根据我国《公路工程结构可靠度设计统一标准》［13］规定取用，抗力及恒载效应的统计参数如表2所示.活载效应由传感器监测数据统计分析确定，以1 个月为计算时段，应变阈值取30×10－6，对应的应力阈值为7.41 MPa，其统计参数如表3所示.

表2 抗力与恒载效应的统计参数Tab.2 Statistical parameters of resistance and dead load effect

表3第2列给出了东海大桥主航道斜拉桥跨中截面基于承载能力极限状态的可靠指标，采用数据为2007年5月到2008年7月共计15个月份.从表3可以看出东海大桥主航道斜拉桥跨中截面抗拉强度可靠指标在15 个月内变化非常小，其最小值为11.53，发生在2007年7月；最大值为11.61，发生在2007年11月，最大变化率（βmax－βmin）／βmin为0.7%.由于每天通过的车辆是随机的，因此这种小幅度的变化是合理的，表明结构状态没有改变.从失效概率上来说，构件实效概率都在10－30以下，因此结构构件是非常安全的.

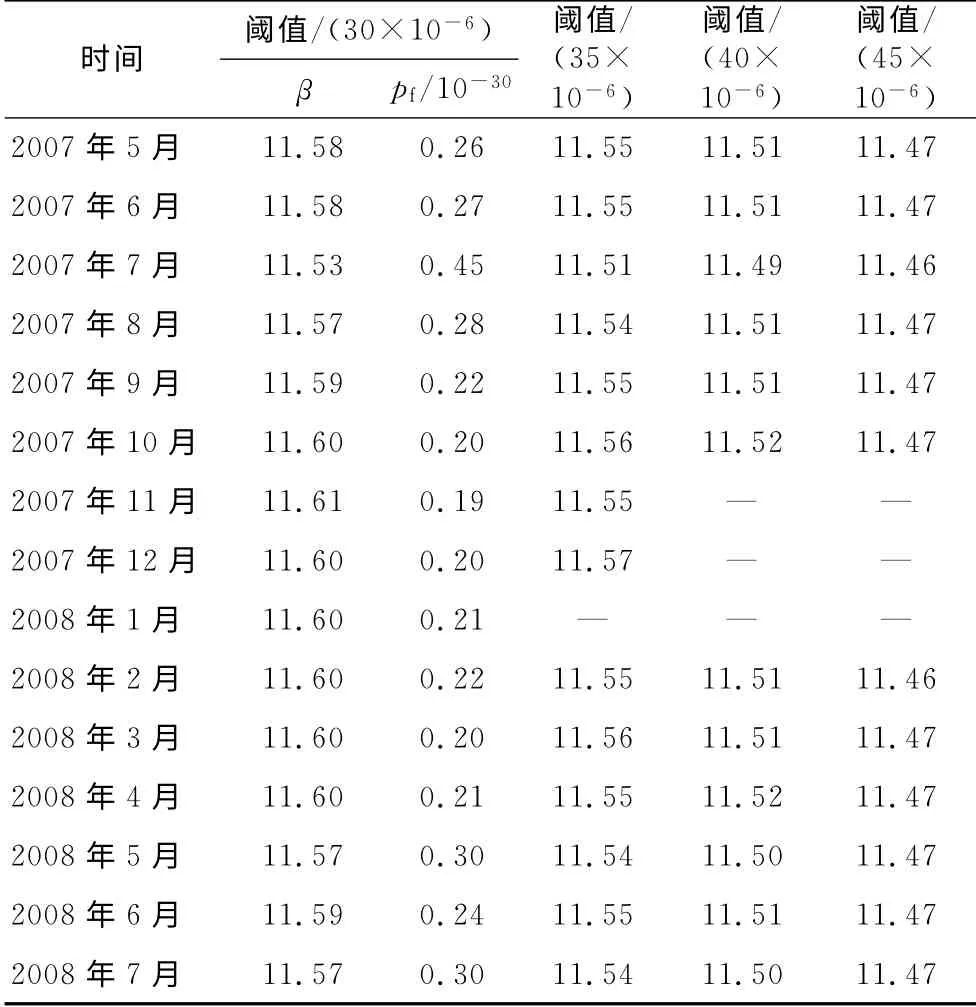
表3 活载效应及构件屈服强度可靠指标Tab.3 Live load effect and member yielding reliability index

为了考察阈值对可靠指标的影响，表3第4—6列还给出了不同阈值下每个月所对应的可靠指标.从表3可以看出，可靠指标随阈值的增大而减少，但是变化幅度很小.研究数据还显示，随着阈值的提高，极大值数据量急剧减小，且数据变异性增大，因此相应计算结果的可信度降低.由于篇幅所限，阈值对可靠指标的影响不做过多论述.

4 结论

本文通过研究监测信号的PSD，利用车桥耦合振动理论，对东海大桥主航道跨中截面纵向应变的特点进行了分析，提出了一种新的监测极值提取方法.文章将上述方法与工程实例相结合，利用东海大桥15个月的应变监测数据对主航道斜拉桥主梁跨中截面的承载能力极限状态进行可靠性分析评估，得到以下结论：

（1）在基于健康监测的桥梁结构可靠性分析中，对于东海大桥来说，移动车辆荷载引起的活载效应对构件可靠性起控制作用.

（2）东海大桥主航道斜拉桥跨中截面屈服强度可靠指标在计算时间区间的变化幅度很小，总体来说冬天可靠指标略微大于夏天可靠指标，主要是因为冬夏温度差别使得冬天的活载应变普遍低于夏天的活载应变.

（3）可靠指标随阈值的增大而减小，但是影响不大.不过，随着阈值的增大，极大值的数据量急剧减小，且数据的离散性增大，这将影响可靠指标计算结果的准确性.

由于篇幅所限，本文在进行可靠性分析时并未考虑温度对可靠指标的影响，在后续工作中将开展温度等环境因素对构件可靠指标影响的研究.另外，如何选择一个合理的阈值也是今后的研究课题之一.

［1］ Catbas F N，Gokce H B，Frangopol D M.Laboratory studies to explore uncertainty quantification for systems－based SHM［C］∥The 10thInternational Conference on Structural Safety and Reliability （ICOSSAR2009）.Osaka：CRC，2009：2123－2128.

［2］ Ni Yiqing，Hua Xugang，Ko J M.Reliability－based assessment of bridges using long－term monitoring data ［J］.Key Engineering Materials，2006（321323）：217.

［3］ Frangopol D M，Strauss A，Kim S.Bridge reliability assesement based on monitoring［J］.Journal of Bridge Engineering，2008，13（3）：258.

［4］ Frangopol D M，Strauss A，Kim S.Use of monitoring extreme data for the performance prediction of structures：general approach［J］.Engineering Structures，2008，30：3644.

［5］ Fangopol D M，Strauss A，Kim S.Use of monitoring extreme data for the performance prediction of structures：Bayesian updating［J］.Engineering Structures，2008，30：3654.

［6］ LIU Ming，Fangopol D M，Kim Sunyong.Bridge safety evaluation based on monitored live load effects［J］.Journal of Bridge Engineering，2009，14：257.

［7］ LIU Ming，Fangopol D M，Kim Sunyong.Bridge system Performance assessment from structural health monitoring：a case study［J］.Journal of Structural Engineering，2009，135（6）：733.

［8］ Frangopol D M，Strauss A，Kim Sunyong.Structural reliability assessment using sensors and Bayesian updating［C］∥The 10thInternational Conference on Structural Safety and Reliability（ICOSSAR2009）.Osaka：CRC，2009：1069－1075.

［9］ Kim S，Frangopol D M.Optimal decision making for structural health monitoring under uncertainty ［C］∥ The 10thInternational Conference on Structural Safety and Reliability（ICOSSAR2009）.Osaka：CRC，2009：621－627.

［10］ Frangopol D M.Life－cycle performance，management，and optimization of structural systems under uncertainty：accomplishments and challenges［C］∥The 10thInternational Conference on Structural Safety and Reliability（ICOSSAR2009）.Osaka：CRC，2009：38－60.

［11］ Ang A H S. On risk and reliability－contributions to engineering and future challenges［C］∥The 10thInternational Conference on Structural Safety and Reliability（ICOSSAR2009）.Osaka：CRC，2009：1－20.

［12］ 贡金鑫，魏巍巍.工程结构可靠性设计原理［M］.北京：机械工业出版社，2007.GONG Jinxin，WEI Weiwei.Reliability design principles of structural engineering ［M ］. Beijing： China Machine Press，2007.

［13］ 中华人民共和国交通部.GB／T 50283—1999 公路工程结构可靠度设计统一标准［S］.北京：中国计划出版社，1999.Ministry of Communications of the People’s Republic of China.GB／T 50283—1999 Unified standard for reliability design of highway engineering structures［S］.Beijing：China Planning Press，1999.

［14］ 闵志华.基于长期监测的斜拉桥状态特性概率性分析［D］.上海：同济大学土木工程学院，2009.Min Z H.Probabilistic analysis of condition properties of cable－stayed bridge based on long－term structural health monitoring［D］.Shanghai：Tongji University.School of Civil Engineering，2009.

［15］ SUN L M，DAN D H，SUN Z，et al.Health monitoring system for a cross－sea bridge in shanghai［C］.Proceeding of IABSE 2006Symposium Budapest，Hungary，2006.

［16］ 李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，2002.LI Guohao.Stability and vibration of bridge structures［M］.Beijing：China Railway Publishing House，2002.

［17］ 赵永刚，盛洪飞，徐世俊.桥面平整度对大跨度斜拉桥车桥耦合振动的影响［J］.石家庄铁道学院学报：自然科学版，2008，21（3）：54.ZHAO Yonggang，SHENG Hongfei，XU Shijun.Effects of bridge deck surface roughness on vibration of large span cablestayed bridges due to moving vehicles［J］.Journal of Shijiazhuang Railway Institute ：Natural Science，2008，21（3）：54.

［18］ 李昆，孙开畅.公路钢桥可靠度设计中结构抗力统计参数分析［J］.钢结构，2008，23（12）：30.LI Kun，SUN Kaichang. Anslysis on the statistical paramenters of resistance of highway steel bridge reliability design［J］.Steel Construction，2008，23（12）：30.