基于DEM的铁路带状数字航空摄影航线优化设计

邓继伟 张 丽

(铁道第三勘察设计院集团有限公司，天津 300251)

航线设计是航空摄影测量任务的基础，设计质量的优劣直接关系到航空摄影测量的作业效率和质量。其主要任务是根据航摄任务书的内容和要求完成分区的航线、像主点的敷设，并将设计的成果提交飞行单位，由飞行单位完成航摄任务［1］。传统的摄影测量多采用等基线摄影测量的方式，这种方式对于平坦地区具有较强的适应性，但对于丘陵、山区等作业区域高程起伏较大的地区，高程的起伏会影响到相邻航空影像的航向重叠度和旁向重叠度［2］。航摄计算时是参照平均基准面设计的，如果针对地形起伏对重叠度的影响考虑不周，可能会产生航摄漏洞或者航片的冗余;传统航线设计基本采用等基线的航线设计方式，该方式一般以整个分区为单位计算地形起伏对重叠度的影响，不能有效顾及到局部相邻像对在地面的实际重叠度。

另外，在传统的铁路带状航空摄影航线设计中，由于存在一定的线划误差，如何准确计算航线偏离线位中线距离，从而合理布设航线，最大化地减小航飞代价也亟待研究解决。在实际工作中，基于数码影像的航空摄影测量航线设计应顾及到数码航摄仪独特的优势和特点，才能设计出合理、可靠的航线。

针对这些问题，提出一种基于DEM航线设计方法，根据地形、相机参数自动设计出最适合该测区的航线，在保证航飞安全的前提下，节约成本，提高经济效益。

1 关键技术

1.1 数码航摄航高的确定

航摄资料主要用于量测和判读，因此摄影比例尺的选择与成图比例尺的大小或航摄资料用于判读时像片的基线放大倍数有关，后者由于各用户单位在提取信息时对判读的具体要求不同，难以提出统一的规定。但航摄资料无论用于量测或判读，总是希望在保证满足使用要求的前提下，尽可能缩小摄影比例尺，以便提高经济效益，降低航摄经费。

现有的摄影测量航摄规范是针对传统胶片航摄方式制定的，因此在数码航摄航线设计采用航摄比例尺确定航高时，须等效为胶片航摄方式进行计算。无论传统胶片式航空摄影测量，还是数码航空摄影测量，它们空中三角测量的地面精度规范是一致的(即物方点高程中误差MZ的限差是一致的)。高程中误差的计算公式如下

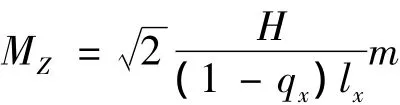
由于地形图航空摄影测量规范中高程中误差限差是固定的，即有M1=M2，在同一重叠度条件下(q1=q2)，数码航摄的航高H2与传统胶片航摄的航高H1有如下关系

其中:对于胶片航摄仪，设高程中误差为M1，航高为H1，重叠度为q1，像点中误差为m1，像片像幅长为l1;对于数码航摄仪，设高程中误差为M2，航高为H2，重叠度为q2，像点中误差为m2，像片像幅长为l2。

1.2 平均基准面高程h基的确定

在航空摄影航线设计中，计算平均基准面高程时，应根据线路中线和航线覆盖的范围绘出测绘工作范围线，即首先确定航摄范围，根据测绘工作边线内的高程来计算h基，这一点和面状设计是一致的。在面状设计中为测区内具有代表性的高点的平均高程和低点的平均高程。铁路线路选线是带状的，覆盖面积小，如果按照面状的计算方法，当最高一点位于测绘工作边线时，将可能造成h基的计算不准确而造成像片旁向覆盖不确定，从而引起航摄绝对漏洞的产生。因此，根据经验，认为对于铁路线状设计，在计算平均基准面高程时，参照面状设计计算方式的同时应考虑测绘工作边线上的高点高程，尽量避免产生航摄漏洞;另外，应重点使用铁路线位附近的高程进行计算，从而保证航摄成图区域内航摄比例尺的适用性。

1.3 确定GSD

所使用的数码相机以及摄区的基本情况确定之后，整个航摄设计的出发点只有一个，那就是GSD，GSD为数码相机CCD一个像元对应的地面尺寸，或理解为数字影像对地面的采样间隔。数字航空摄影进行航飞设计时，首先要确定GSD。

GSD的确定主要有以下三种方法:

一是由甲方在合同中指明。

二是采用航摄比例尺确定，但须等效为胶片的扫描像元(通常为21μm)来进行计算，例如要求航摄比例尺为1∶3 500时，GSD 应为 3 500×21μm，即73.5 mm。

三是由成图比例尺根据经验来确定。例如1∶500为6～8 cm，1∶1 000为10 cm;特种成图比例尺GSD应有所调整，例如1∶500地籍界址点测量时，应采用4～5 cm的GSD。

总之，GSD的确定要根据具体情况，最终与甲方共同确认。

2 基于DEM的航线设计

航线设计是航空摄影的前期准备，设计质量的好坏直接影响到后续工作的进行。只有按照相关规定和要求设计出好的航飞方案，才能保证实际航飞顺利准确地进行，满足用户的实际需要。以下的航线设计方法主要分航线粗略定位和精确敷设两步进行。

2.1 航线粗略定位

(1)当摄影区域的面积较大时，将受到飞机续航时间和太阳光照及太阳高度角的限制，不可能通过一次飞行就完成整个摄区的航摄任务。由于航摄领航技术的限制，摄影航线不能太长，否则就难以保持航线的直线性及航线间的平行性，影响航摄飞行质量。因而当航线较长或摄区内地形变化较大时，应将摄区划分成若干个摄影分区，在每个分区内用不同航高进行摄影，以保持像片比例尺的一致。

(2)根据DEM计算每个摄影分区的平均基准面高程。

(3)根据航测成图范围及航线的容许摆动范围要求，确定所设计航线的覆盖范围。

例如在铁路勘察设计中，一般根据线路专业提供的线位进行外扩从而确定测绘工作范围线。根据线位沿线带状测绘范围的宽度计算每一测段需要几条航线;在确定航线数的时候应考虑实际飞行状况，如果没有侧风影响，飞机将按设计的航线直线飞行，但当有侧风影响的时候，飞机将会出现一定的摆动，在航线设计时应将此考虑进去，较精确地界定航线的覆盖范围，从而做出粗略的航线定位。

2.2 变基线的航线精确敷设

航线设计的主要目的在于确定每个曝光点的位置，从而为航拍员提供指导。在划分好航摄分区及遵循地形图航空摄影规范的基础上，选择合适的摄影比例尺，采用逐摄影中心调整基线的方法确定最佳的曝光点位置，具体设计方法如下:

(1)根据摄影分区的DEM确定航线的位置，即确定航线的起点和终点，起点和终点满足航向超出分区不少于一条基线，旁向满足航摄成图范围要求即可(一般为超出分区不少于像幅的50%)。

(2)航线上摄影中心位置的确定，这是航线敷设的关键所在。

根据测图比例尺的要求，选择合适的航摄比例尺，进而确定飞机的摄影航高。

确定每条航带的第一个摄影中心的位置:第一条航带的第一个摄影中心就是航线的起点。从第二条航带开始，每条航带的第一个摄影中心的确定方法为:如果该航带的影像与相邻上一条航带的影像在设计重叠度的旁向重叠区域平均高程低于平均基准面高程，则该航带第一个摄影中心与上一条航带第一个摄影中心间隔为设计重叠度在平均基准面上计算出来的旁向基线长。由于在分区时已经考虑到地形高差的影响，此时影像不仅满足重叠度要求，而且分辨率也肯定能达到精度要求，用设计的基线长即可，无须调整。

如果旁向重叠区域高程高于平均基准面高程，则需调整基线长:地面点的实际旁向重叠度为设计旁向重叠度，从而计算出在平均基准面上的新旁向重叠度Py，以及其对应的旁向基线长Dy，进而即可算出该航带第一个摄影中心的空间位置。Py及Dy的计算公式［3，5］如下

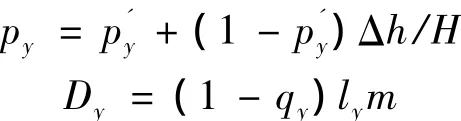
式中:ly为航摄相片旁向的像幅尺寸;Δh为相对于摄影基准面的高差。

确定每条航带上第二个及以后每个摄影中心的位置:在同条航带上，如果航向相邻两张影像在设计重叠度的航向重叠区域高程低于平均基准面高程，则该摄影中心与上一摄影中心间隔为设计重叠度在平均基准面上计算出来的基线长。如果航向重叠区域高程高于平均基准面高程，则需调整基线长:地面点的实际航向重叠度为设计航向重叠度，从而计算出在平均基准面上的新航向重叠度qx对应的航向基线长Bx，进而即可算出该摄影中心的空间位置。qx及Bx的计算公式［3］如下

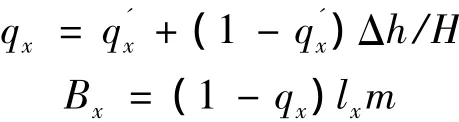
式中:lx为航摄像片航向的像幅尺寸。

以上所述是根据测区地形起伏，在航带间以第一张像片为基准调整整条航带与相邻航带的间隔，航带内调整相邻两曝光点之间的基线长，从而使得相邻两张像片覆盖的实际地面的重叠度满足设计重叠度的要求，减小了地面起伏对重叠度的影响。整个测区的每个曝光点的空间位置都被计算出来，即已完成给定重叠度的航线设计。

3 实验及效果分析

为了更加直观地理解基于DEM的航线设计方法，就生产中的一个项目进行实验，具体分析如下:

该实验区选自东北地区某条改建铁路的一段，此线路以山区为主，地形等级主要为Ⅲ级，部分为Ⅳ级，按照线路及站场专业的要求，沿线位两侧各外扩3 km设计，以满足1∶2 000及1∶10 000地形图的成图要求。

本实验选用传统航线设计与本文优化航线设计两种方式，用于比较分析。其中，相机焦距92 mm，航向像幅79.206 4 mm，旁向像幅87.091 2 mm，像素大小5.6μm。传统航线设计中，相对航高为1 520 m，航向及旁向重叠度分别为60%和30%，分为7个测段，共73条航带，2 272张航片。优化航线设计中，相对航高为1 520 m，航向及旁向重叠度分别为60%和30%，分为4个测段，共38条航带，1 988张航片，航线设计对照如图1所示。

在航带设计中采用模拟数据解算的方式，即根据DEM、模拟所得的内外方位元素文件及像点坐标文件进行多片前方交会平差解算，然后对平差结果做精度分析。实验中，像点坐标加上的残差是以2μm为中误差的高斯随机误差，外方位元素的线元素和角元素加上的残差分别是以0.015 m和0.000 1 rad为中误差的高斯随机误差。按1∶2 000比例尺地形图国家规范及铁路工程摄影测量规范要求，分析点位的平面与高程精度，传统航线设计与优化航线设计对照如表1所示。

表1 传统航线设计与优化航线设计对照

在传统航线设计中，采用的是等基线布设的方式，由于测区地面起伏较大，最高点和最低点的航向重叠度分别达到了51%和70%;另外，第七测段主要Ⅳ级地形，航线设计中该测段的设计航向与旁向重叠度分别为65%和35%才得以满足要求。而本文的优化设计中，通过变基线布设的方式，使得地面每个区域的实际航向重叠度都保证在60%左右，严格按照设计重叠度进行布设，从理论上减小了航摄漏洞出现的可能。

根据1∶2 000比例尺地形图国家规范，Ⅲ级地形图上点位平面限差为2.4 m，高程限差为1.6 m。由表1可知，当航线设计试验中模拟的像点误差、外方位元素误差与实际飞行数据基本一致时，使用相同的相机和测区进行航线设计，在精度都能达到要求的基础上，采用优化设计方法减少了共3测段，35条航带，284张像片，有效提高了航飞效率。

另外，如果在传统航线设计中也顾及地面起伏，使最高点区域的重叠度也保证在设计重叠度60%，则设计时基准面上的重叠度必将大于60%。选取本文实验项目的其中一条航线中的一段分别进行传统等基线设计与优化变基线设计，两种设计方法使用相同的航高1 520 m，最高区域均满足60%的航向重叠度，相对于平均准面的基线长计算和比较如表2所示。

表2 传统航线设计与优化航线设计基线长对照

选取的这段区域地形起伏较大，在传统等基线设计中，若满足最高区域的重叠度达到60%，则基于平均基准面的设计重叠度达到66%才能满足要求。从表2的对比中可以看出，使用传统等基线的设计方法，在非最高区域一定程度上造成了影像过分重叠，从整个测区航线设计来看势必会造成航片的冗余，加大了内外业工作量。

4 结束语

通过试验可知，在成功稳定的曝光基础上，该航线优化设计方法能够通过变基线摄影测量的方式保证地面实际重叠度与设计重叠度相一致，并能合理准确地计算出每张像片的摄影中心位置，为外业实拍提供指导。另外，传统的航拍采用的都是手动曝光和定时曝光的飞行控制方法，这种方式存在很多局限性;随着航空摄影技术和手段的不断完善，智能定点曝光的全数字航空摄影测量飞行控制会越来越多地被应用。因此，充分利用现有设备和技术合理做好航线设计，将会有利推动航空摄影技术的进一步发展。

［1］谭成国，范业稳，司顺奇．基于DEM的地理坐标系下航空摄影技术设计［J］．测绘科学，2008，33(2)

［2］段福洲，宫辉力，朱 琳．变基线数字航空摄影航线设计与飞行控制—基于DEM的设计方法［J］．自然灾害学报，2008，17(6)

［3］张剑清，潘 励，王树根．摄影测量学［M］．武汉:武汉大学出版社，2003

［4］乔瑞亭，孙和利，李 欣．摄影与空中摄影学［M］．武汉:武汉大学出版社，2005

［5］GB/T19294—2003 航空摄影技术设计规范［S］