磁流变阻尼器减震控制算法设计

鲍祖尚，胡潇潇

(长沙师范学校，中国 长沙 410100)

磁流变阻尼器是电可控元器件，通过改变其输入电压或电流来改变其阻尼系数，从而起到耗能减振的目的．而如何来改变其输入电流，这就需要一定的控制算法，根据结构状态参数的变化，控制阻尼器输入的电流值[1]．根据现代控制理论和李亚普诺夫稳定性理论中开关控制算法一般可得出阻尼器的最优阻尼力，为此本文选择了对阻尼器和减振结构的数学模型依赖性较弱并且能直接得到阻尼器输入电流的开关控制算法作为实际控制策略．

在进行控制算法的设计和仿真研究中，依据磁流变阻尼器的数学模型可准确反映阻尼力与速度、电流或电压的关系[2-4]．因为磁流变阻尼器是电可控器件，通过它可以找到阻尼力与输入电流或电压的关系．由于磁流变液本身的非线性特性和在磁流变阻尼器中复杂的流变特性，因此一般建立所谓“现象模型”来反映阻尼器的动态特性．“现象模型”较常用修正Bouc-Wen模型．通过开关控制算法模拟磁流变阻尼器从而得出所谓的智能模型．

1 修正Bouc-Wen模型

为了能反映磁流变阻尼器在低速区域的复杂动态特性，Spencer在Bonu-Wen模型的基础上进行改进，提出了所谓的现象Boun-Wen模型，这里将其称为Spencer模型，其数学表达式如(1)所示[5]：

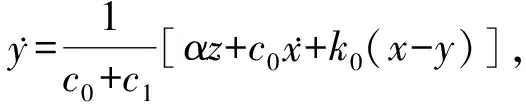
(1)

同时Spencer等人将参数α、c0和c1与输入电压相联系，建立起另一套与电压联系的微分方程组如式(2)所示：

α=α(u)=αa+αbu，

c1=c1(u)=c1a+c1bu，

c0=c0(u)=c0a+c0bu，

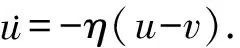
(2)

通过求解微分方程组(1)和(2)可以得到在不同输入电压、不同速率下的阻尼力[6]．Spencer模型能比较精确的反映磁流变阻尼器的动态特性，所以许多学者将其作为研究使用．利用文献[7]所提供的实验数据和参数辨识结果，根据方程组(1)和(2)在Matlab/Simulink中建立的Spencer模型如图1所示：

图1 在Matlab/Simulink中建立的Spencer模型

2 减振结构数学模型及开关算法

2.1 减振结构数学模型

本文研制的是一维减振台，其可以简化为一维的弹簧阻尼振动模型，如图2所示：

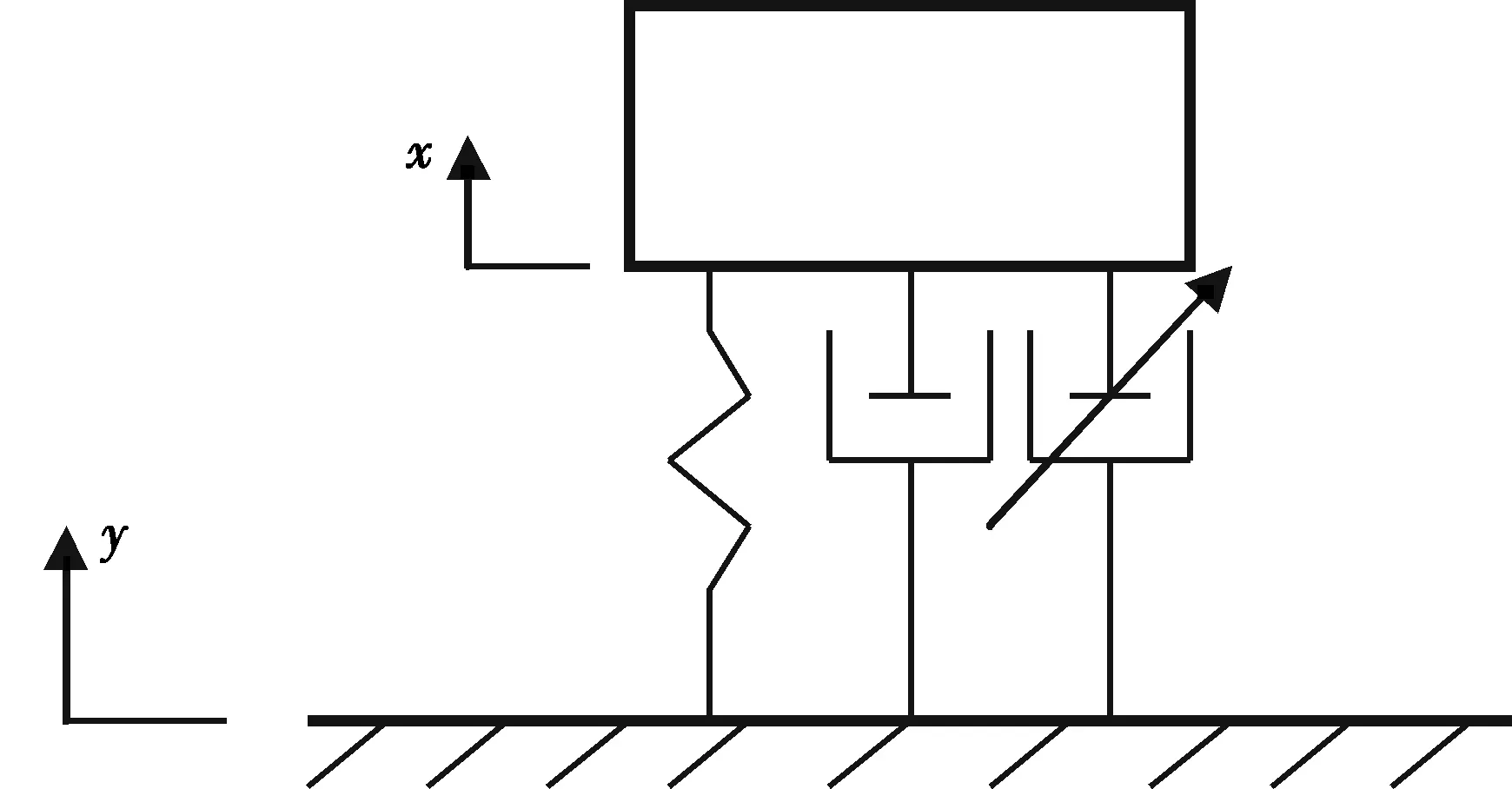
图2 一维减振台简化模型

模型由被减振对象即重物、弹性元件、固定阻尼和可变阻尼组成[8]．弹性元件代表弹簧的作用，固定阻尼主要体现了传动部件的阻尼力，可变阻尼代表磁流变阻尼器．y为振源激励的位移，x为被减振对象即重物的位移．简化模型的数学表达式如下：

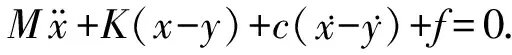
(3)

式中M为被减振对象;K为弹簧弹性模量;c为传动部件的阻尼系数可忽略为零;f为磁流变阻尼器阻尼力(N)．

2.2 开关控制算法

本文选取了的开关控制算法作为具体的控制策略，这种控制算法能直接得到磁流变阻尼器需要的输入电流值．

开关控制是从滑模控制理论推导而来[8],其常用的数学形式为：

(4)

式中f为磁流变阻尼器的阻尼力(N);u为阻尼器缸体相对于活塞的位移(mm)．

这种控制方法也常称为双态控制．因为fmin出现在输入电流或电压为最大；fmax出现在输入电流或电压为最小的状态．

从结构振动的物理意义上来理解，当结构体如弹簧阻尼质量系统，受到激励作用开始阶段，结构相当于受到一个冲击作用，这时候我们希望结构体内部的阻尼比较小，整个结构刚度比较“软”，起到一定缓冲吸振作用；在冲击作用中，结构受到力的作用，有一定的加速度，同时接收了激励一部分能量，有一定的动能．在随后过程中结构体会有一段加速过程速度增大，这时候我们希望结构体内部的阻尼比较大，起到摩擦耗能的作用，减少结构体内部的拉伸分离，减少破坏．在振动开始阶段，有可能对阻尼器施加了电流或电压，使结构刚度变硬，从而使结构体在振动初期受到更大冲击作用，产生结构振动局部放大现象．针对这种问题，有的学者提出了改进开关控制，其表达式如式(5)所示：

(5)

式中 [u]为相对位移阈值(mm)．

改进开关控制的策略是，如果结构远离平衡位置，并且当结构的顶层位移超过某一位移时，才将电流开启，施加最大控制力；其他情况将电流关闭，施加最小控制力．这种控制算法能有效解决局部振动放大的问题．但阈值[u]、最大电流Imax的取值缺少依据，主要靠经验或反复试验调试，比较难把握．同样，根据实际需要不一定将阻尼器实际可输入的最大电流作为控制算法的最大电流，否则也可能会产生冲击．但总的来说，开关控制算法结构简单，无论在软件或硬件上都比较容易实现，实用价值比较大．

2.3 开关控制算法设计

开关控制算法的常规表达式如(5)所示，需要两个物理量，一般选取阻尼器缸体相对于活塞的位移或速度作为控制输入状变量．本课题研制的减振平台因为阻尼器缸体与振源紧固连接，缸体运动参数和振源运动参数一致；而活塞杆与重物紧固连接，所以阻尼器缸体相对于活塞的运动实质上为振源相对于重物的运动．其中一个输入变量选择为重物相对于振源的速度．同时考虑到，在活塞相对于缸体的速度接近零时，即在振动末期，结构可能受到扰动激励，如果这时仍然施加电流，可能会因结构刚度较大而增大扰动激励的作用．因此这里的另外一个输入变量选择为重物速度，代替改进开关控制算法的相对位移量．使用重物速度能同时考虑到振动开始和末期可能产生的局部振动放大现象．开关控制算法的表达式为式(6)．

(6)

式中u为被减振对象，重物速度(mm/s)；v为活塞相对缸体的速度，亦即重物相对振源的速度(mm/s)；[v]为重物速度阈值(mm/s)．

这里将最小电流设为0.001 A主要是考虑防止计算机意外输出一个较大值作为零值．

3 开关控制算法仿真实验

利用修正Bouc-Wen模型建立的Spencer模型，和减振平台的数学模型见式(4)，在Simulink中构建开关控制算法的仿真模型，如图2所示.

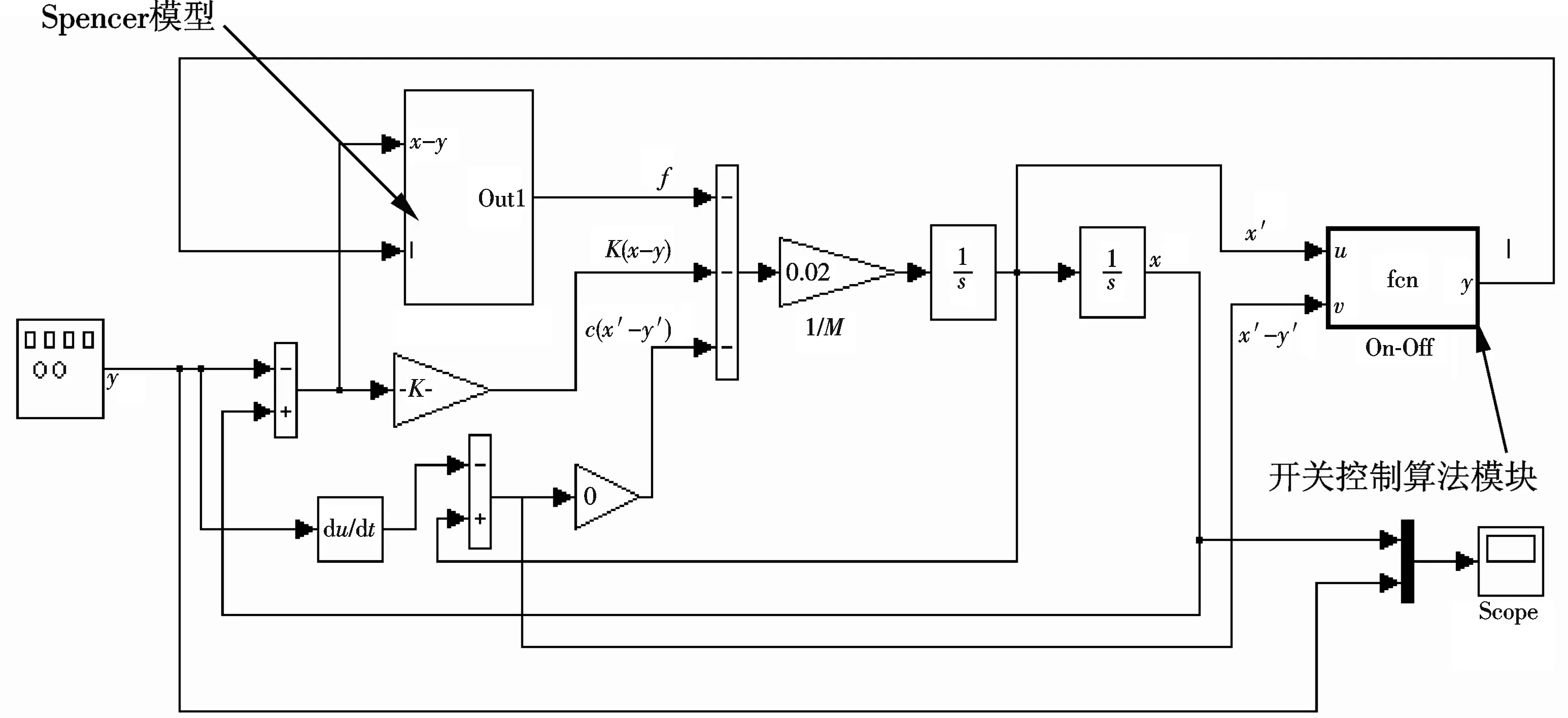
图2 开关控制算法仿真模型图示

开关控制算法模块是一个用M函数编写的自定义函数模块．将Spencer模型封装成一个子系统嵌入到仿真模型中．对模型输入幅值为12 mm，周期为400ms的正弦激励；Simulink解算器设为固定步长0.001，解算器选择为“ode5”，时长设定为3ms进行仿真． 当Imax设定为0.5 A，V分别为0 mm/s、20 mm/s、40 mm/s、100 mm/s时得到的位移仿真图像如图3所示．

当V设定为0 mm/s，将电流值分别设定为0.1 A、0.2 A、0.5 A、1.0 A的仿真结果如图4所示.

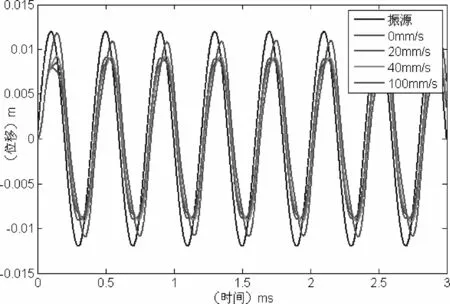
图3 不同速度阈值的位移仿真结果

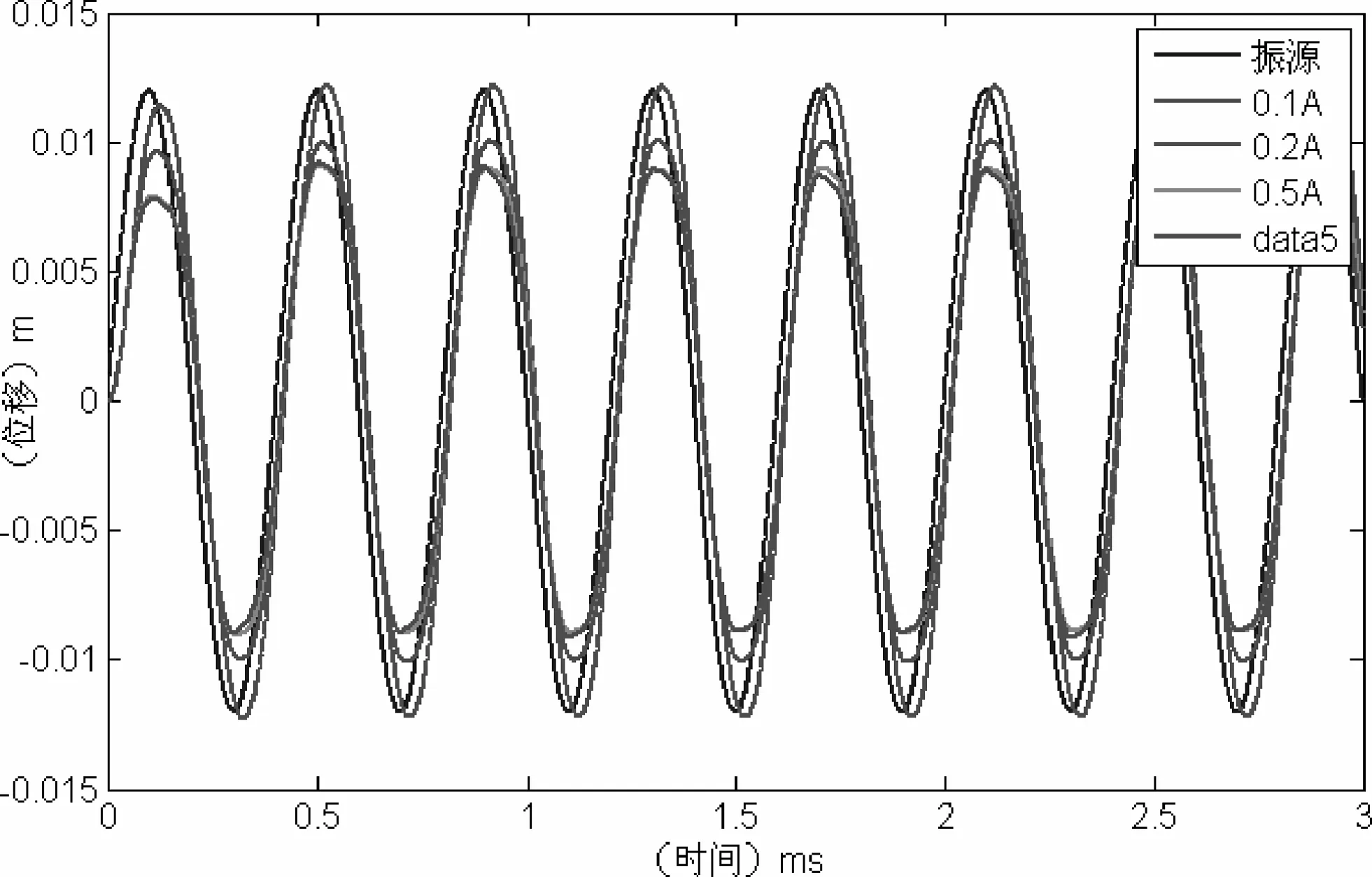
图4 不同电流值的位移仿真结果

由仿真结果来看，对于速度阈值V，当V=0时，控制效果较好；对于输入电流值，电流值越大，控制效果越好．但经过实际反复控制实验，实际上是当V取值为50 mm/s，电流取值为0.35 A时，控制效果比较好．

4 结论

本文在分析现有控制算法的基础上，选择了比较容易实现的开关控制算法作为减振平台的控制策略．在Mtalab平台中设计了开关控制算法．并对算法进行了仿真，在仿真中验证了开关控制算法的有效性．但磁流变阻尼器的数学模型是参照相关文献数据得到的，因此所设计的控制算法还要在实际控制中进行检验和修改．

参考文献：

[1] 关新春，李金海，欧进萍. 不同规格磁流变阻尼器的磁学与力学特性[J]. 功能材料, 2006, 37(7):1169-1172.

[2] 方子帆，邓兆祥. 磁流变阻尼器简化力学模型研究[J]. 工程力学,2007,24(11):32-35.

[3] 汪小华, 张培强. 磁流变液阻尼器的模糊逻辑非参数建模[J]. 中国科学技术大学学报, 2000,30(2):218-220.

[4] 任晓崧，凌海梅. MR阻尼器的半主动控制研究[J]. 力学季刊, 2001,22(4): 471-476.

[5] 王鸿云,郑惠强,李泳鲜.磁流变液的研究与应用[J].机械设计,2008,25(5):1-4.

[6] 贾永枢，周孔亢. 车用磁流变液流变特性分析和研究[J].机械工程学报,2009,45(6): 246-249.

[7] RASHID M M, HUSSAIN M A, RAHIM N ABD. Application of magneto-rehological damper for car suspension control[J]. J Appl Sci, 2006, 6(4):933-938.

[8] WEN Y K. Method for random vibration of hysteretic systems[J].J Engin Mech Divi, 1976,102(2):249-263.