底部出电型铝电解槽母线结构与电磁流场仿真优化
刘业翔, 梁学民,, 李 劼, 张红亮, 徐宇杰, 丁凤其, 邹 忠
(1. 中南大学 冶金科学与工程学院,长沙 410083;2. 河南中孚实业股份有限公司,巩义 451200)
底部出电型铝电解槽母线结构与电磁流场仿真优化
刘业翔1, 梁学民1,2, 李 劼1, 张红亮1, 徐宇杰1, 丁凤其1, 邹 忠1
(1. 中南大学 冶金科学与工程学院,长沙 410083;2. 河南中孚实业股份有限公司,巩义 451200)
从减小槽内水平电流和垂直磁感应强度进而改善磁流体稳定性的角度出发,提出一种底部出电型结构铝电解槽,该种电解槽采用阴极垂直出电方式代替传统水平出电方式。在ANSYS软件平台上,建立400 kA级该槽型的电磁场模型并进行求解,根据计算结果对母线配置进行优化,得到一种可使磁场分布最优的母线结构,在该母线配置下,垂直磁感应强度最大值为1.658 mT,平均值为0.401 mT,远低于同规格普通电解槽,磁流体稳定性计算结果进一步表明该槽能在低极距下稳定运行,具有较大的节能潜力。
铝电解; 母线优化; 多物理场
现代铝电解理论表明,铝液中水平电流和垂直磁场相互作用引起的电磁力是影响铝电解槽内磁流体稳定性的主要因素[1],而水平电流和垂直磁感应强度的大小及分布取决于电解槽及母线的结构设计。
在传统铝电解槽内,电流由阴极底部的水平钢棒从两侧导出,再经阴极母线汇集至下一槽的立柱母线。母线结构的合理设计是实现槽内电磁场优化的关键,这一方面国内外学者进行了很多研究。早期,TVEDT和NEBELL[2]以及BUIZA[3]分别开发名为“NEWBUS”和“BUSCAL”的 1D 线单元母线模型,并通过求解电热耦合方程进行母线系统的设计与优化。KACPRZAK等[4]开发了电解槽及母线的3D实体电磁场计算模型,以调整和优化 100 kA槽阴极软母线中的电流分布。DUPUIS和BOJAREVICS[5]开发基于ANSYS软件的3D实体母线模型和基于 TECPLOT软件的 1D槽内导体和母线系统模型,进行 500 kA槽的母线电流优化。同时,不少学者从母线优化效果的角度开展磁场计算方法的验证工作[6−8],国外学者报道有关使用三维结构的母线设计或优化模型[9−10],研究 100 kA 和500 kA预焙槽母线系统的电流均匀分布问题。近些年来,李茂等[11]则应用遗传算法对母线进行优化计算,该方法能得到最优化的母线结构,但该方法亦存在优化计算过程时间较长和母线参数的设置复杂等不足。
对于底部出电型铝电解槽的研究,国内外目前进行得很少,鲜有文献报道,更多的是一种概念化电解槽,其中,PETERSON等[12]提出了一种“蘑菇状”阴极导流型铝电解槽,采用蘑菇状可润湿性阴极,但该槽型的阴极材料抗腐蚀和耐冲击性能难以达到工业化要求;GEORGES和NORA[13]在其专利中提出了一种采用惰性阳极的导流槽,采用聚铝沟沟型阴极,阴极导杆处于槽底阴极块的几何中心处,但也存在阴极易于早期破损的问题;此外,还有不少竖式铝电解槽,部分结构也采用将电流从底部导出[14]。
本文作者提出一种有别于传统结构的 400 kA级底部出电型铝电解槽,在ANSYS有限元平台上,根据由简到繁的过程,对新型槽母线配置进行系统优化研究,得到最优化的母线结构,最后通过研究电−磁−流场和磁流体的稳定性,验证该电解槽的巨大节能潜力。

表1 400 kA预焙铝电解槽的主要结构参数Table 1 Main structure parameters of 400 kA reduction cell
1 底部出电型铝电解槽结构及母线优化
1.1 结构简介
传统铝电解槽的阴极钢棒为水平放置,电流经阴极炭块在阴极钢棒汇集后,沿水平方向流出电解槽并连接至阴极母线,如此则产生较大的水平电流,造成电解槽内铝液波动,从而降低电解槽的电流效率。为此,本文作者提出一种底部出电型铝电解槽,即将传统水平钢棒改变成为水平−垂直组合的形式,电流经过垂直钢棒从电解槽底部导出,从而大大降低槽内的水平电流。
底部出电铝电解槽除阴极炭块、钢棒及槽周围母线外,其他结构与现行普通400 kA铝电解槽结构基本一致,其主要结构参数如表1所列,其阴极钢棒与母线的连接如图1所示。

图1 阴极钢棒结构示意图Fig.1 Schematic diagram of structure of cathode bar
1.2 母线结构设计
与传统结构槽相同,母线设计对本新型结构槽内电磁场的优化至关重要。为此,本文作者遵循由简至繁的设计理念,从最简单的连接方式,逐渐引入底部母线补偿和端部母线补偿,再考虑出电母线间的相互抵消作用,直至得到最优化的母线设计方案,该过程如图2所示。在整个过程中,总共设计了几十种母线结构,记为 SG1−SG31,根据其磁场分布的特点及大小,对母线配置进行评价。由于篇幅所限,本研究仅选出其中有代表性的4种方案,如图3所示,其中,SG1为根据最初底部出电思路得到的母线最简单结构,SG7为具备端部磁场补偿的母线结构,SG19为同时具备端部与底部磁场补偿的母线结构,SG31为最终经过各种优化后的母线结构。
在设计过程中,发现电解槽电场结果基本类似,因此,本研究中仅列出SG31的电场结果。此外,在磁场方面,对槽电压与电流效率影响最大的为垂直磁场,因此,仅列出各种母线配置下的槽内垂直磁场的仿真结果。
2 电磁流场仿真模型
2.1 电场的计算原理与模型
由于为电解槽供电的整流电源可以近似认为是一个恒流源,故铝电解槽内电场也可以近似认为是一个稳恒电场,电流满足欧姆定律和守恒方程:

式中:J是电流密度, A/m2;E是电场强度, V/m;σ是电导率, S/m。利用矢量等式∇×(φ∇)=0,获得标量电势φ与电场强度E之间的关系φ-∇=E,即可求解出电场分布[15]。计算所用有限元网格模型如图4所示,钢棒与母线及阴极的连接如图5所示。

图2 母线设计流程Fig.2 Flowchart for bus bar design
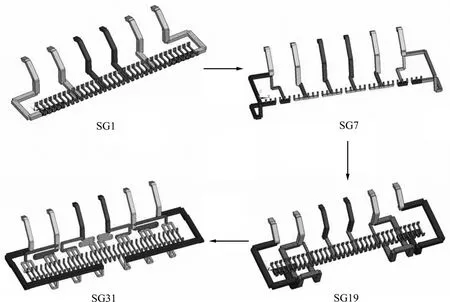
图3 母线结构的设计和演变Fig.3 Design and optimization of bus structure

图4 3台实体槽及槽周母线电场计算有限元网格模型Fig.4 Finite element mesh model of three cells and near by bus for calculation of electric field

图5 阴极钢棒与阴极炭块示意图Fig.5 Schematic diagram of cathode steel bars and cathode carbon blocks
电场边界条件如下:在电源正极方向上的横梁母线进电位置上施加电流;在电源负极方向上6个阳极立柱上施加零电势,采用标量电位求解电场。
2.2 磁场的计算原理与模型
铝电解槽内外电流源复杂,且含有大量的磁介质,这使得磁场计算难度大大增加。电场分布求解合理与否直接影响到磁场的求解精度。本研究采用GP ψ-DP三步标量磁位法求解磁场。铝电解槽的磁场问题满足稳态麦克斯韦方程组:

式中:H为磁场强度,A/m;J为电流密度,A/m2;B为磁场感应强度,T;µ为磁导率,N/A2。
磁场计算的网格模型如图6所示。磁场边界条件如下:铝电解槽磁场求解属于开域问题,假设有限空气的外表面处于无限远处,在外边界的节点上施加零磁标量位,即Dirichlet边界条件[16−17]。
2.3 流场及稳定性计算原理与模型
铝电解槽内熔体是不可压缩粘性流体,其运动属于典型的湍流运动。本研究应用非线性浅水模型,通过耦合全槽三维仿真获得的电磁场分布,对该槽内熔体运动进行动力学分析,并考察该槽不同极距下的磁流体稳定性。具体模型及计算流程见文献[18]。

图6 7台槽及槽周母线磁场计算有限元网格模型Fig.6 Finite element mesh model of seven cells and near by bus for calculation of magnetic field
3 仿真计算结果与分析
3.1 电场
本研究计算并分析不同母线配置下400 kA槽底出电槽的电场结果,发现在母线设计遵循电阻平衡的前提下,电场结果并未随母线结构变化而呈现较大变化。故本研究选取最终母线设计方案SG31的电场结果进行分析。
以中间槽作为目标分析槽,计算所得的各部分电压分布列于表2,为进行对比,本研究亦对传统400 kA槽进行电场计算,其各部分电压值如表2所列。
对比发现,传统槽铝液层压降有14 mV,而底部出电槽的铝液层压降只有4 mV,故相比于传统槽,该槽阴极压降也有显著下降。
3.2 磁场
磁场为母线优化的主要判别依据,故采用三步标量磁位法,计算了母线优化(SG1−SG31)过程中所有相应母线配置下的磁场分布,在此,仅给出具备代表性的几种母线配置所对应的磁场计算结果,同时给出传统结构400 kA槽的磁场计算结果。铝液层空间3个方向上磁场的最大值、平均值以及对应的母线用铝量如表3所示。图7和8所示分别为方案SG31和传统结构槽中铝液的磁场分布情况。
磁场计算结果表明: SG31的磁场分布十分理想,其中,Bz的最大绝对值仅为1.658 mT,平均值为0.401 mT,二者都比传统结构槽的小很多。另外,尽管该方案母线用量比传统槽增加了约3 t,但相比SG19等方案,用量则大大减少。因此,综合磁场结果来权衡,SG31为一种比较优化的方案。
3.3 磁流体稳定性
通过母线优化得到最优化方案SG31,本研究应用非线性浅水模型分析该槽在极距分别为5 cm和4 cm情况下的铝液−电解质界面瞬态波动及熔体瞬态流场。5 cm和4 cm极距下磁流体的稳定性计算结果分别如图9和10所示。图中,ζm/h表示界面平均波动量(ζm)与极距(h)的比值,t表示时间。
从图9和10可以看出,当极距为5 cm时,铝液−电解质界面波动很小;而当极距降为4 cm时,磁流体稳定性仍然良好。另外,槽内铝液流场能很快形成稳态,其流动形态为典型的对称两涡流,最大流速和平均流速分别为18 cm/s和4.8 cm/s。从这一计算结果看,槽底出电400 kA电解槽能在很低的极距下稳定运行,能大幅降低槽电压,节能潜力巨大。

表2 传统槽与研究槽的电场结果对比Table 2 Comparison of electric field results of conventional and proposed cells

表3 不同母线配置下磁场分量的比较Table 3 Comparison of magnetic results of different bus structures

图7 SG31的铝液层磁感应强度分布Fig.7 Magnetic flux density distribution of aluminium layer of SG31: (a) Bx; (b) By; (c) Bz

图8 传统400 kA槽的铝液层磁感应强度分布Fig.8 Magnetic flux density distribution of aluminium layer of conventional 400 kA cell: (a) Bx; (b) By; (c) Bz
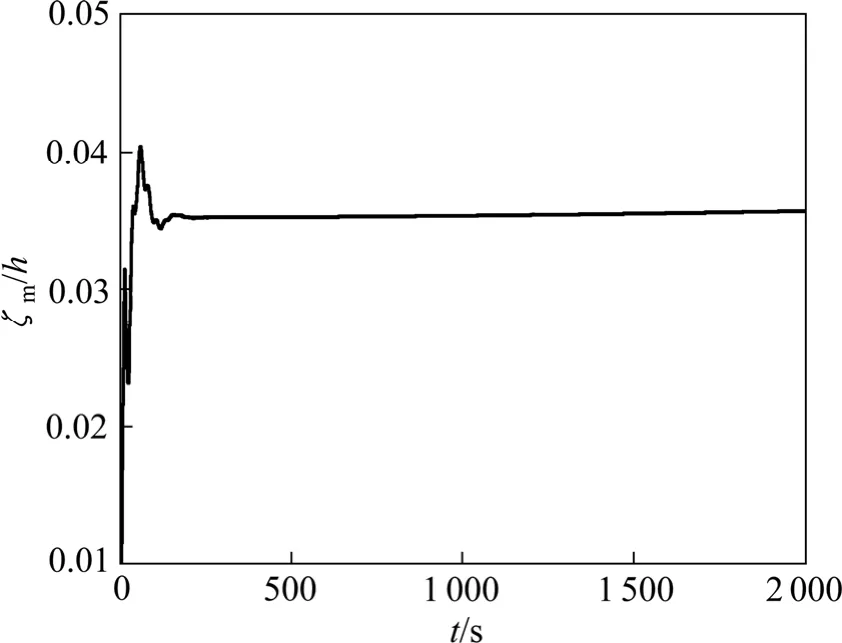
图9 极距为5 cm时铝液−电解质界面波动情况Fig.9 Aluminum-electrolyte interface wave curve at anode cathode distance of 5 cm
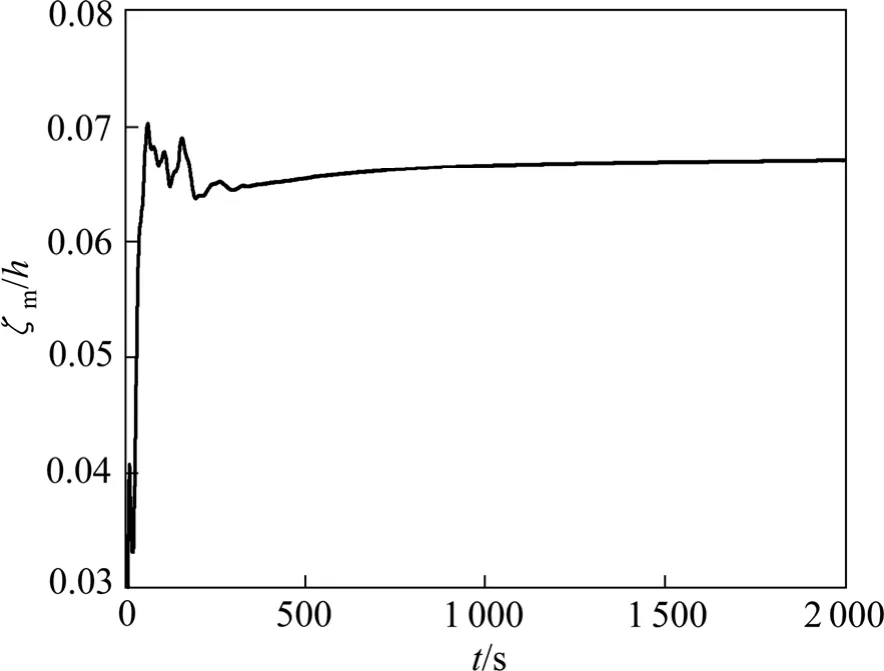
图10 极距为4 cm时铝液−电解质界面波动情况Fig.10 Aluminum-electrolyte interface wave curve at anode cathode distance of 4 cm
4 结论
1) 从减小槽内水平电流和垂直磁场进而改善磁流体稳定性的角度出发,提出一种底部出电型结构铝电解槽,该种电解槽采用阴极垂直出电的方式代替传统的水平出电方式。
2) 对底部出电型铝电解槽进行了母线设计,通过物理场优化,得到一种最佳的母线配置设计方案。
3) 在最佳的母线配置方案下,垂直磁场 Bz绝对值的最大值为1.658 mT,平均值为0.401 mT,该最大值和平均值比水平出电槽的小很多。
4) 磁流体稳定性计算也显示,该电解槽在低极距下还能维持较高的稳定性,具备较大的节能空间。
REFERENCES
[1] LINDSAY R I, DAVIDSON P A. Stability of interfacial waves in aluminum reduction cell[J]. J Fluid Mech, 1998, 362: 327−331.
[2] TVEDT T, NEBELL H G. Newbus, a simulation program for calculation of the current distribution in the bus bar system of alumina reduction cells[C]//BOXALL L G. Light Metals.Phoenix, AZ: Metallurgical Soc of AIME, 1988: 567−573.
[3] BUIZA J I. Electromagnetic optimization of the V-350 cell[C]//CAMPBELL P G. Light Metals. Las Vegas, NV:Metallurgical Soc of AIME, 1989: 211−214.
[4] KACPRZAK D, GUSTAFSSON M, LI L, TAYLOR M.Numerical analysis of the collector bar current distribution of a reduction cell[C]//GALLOWAY T J. Light Metals. San Antonio,TX: TMS, 2006: 367−369.
[5] DUPUIS M, BOJAREVICS V. Weakly coupled thermo-electric and MHD mathematical models of an aluminium electrolysis cell[C]//KVANDE H. Light Metals. San Francisco, CA: TMS,2005: 449−454.
[6] BLANC J M, ENTNER P. Application of computer calculations to improve electromagnetic behaviour of pots[C]//MCMINN C J.Light Metals. Las Vegas, NV: Metallurgical Soc of AIME, 1980:285−295.
[7] SEVERO D S, SCHNEIDER A F, PINTO E C V, GUSBERTI V,POTOCNIK V. Modeling magnetohydrodynamics of aluminum electrolysis cells with ANSYS and CFX[C]//KVANDE H. Light Metals. San Francisco, CA: TMS, 2005: 475−480.
[8] 周 萍. 铝电解槽内电磁流动模型及铝液流动数值仿真的研究[D]. 长沙: 中南大学, 2002: 76−85.ZHOU Ping. A research on mathematical models of electromagnetic hydrodynamics and numerical simulation of metal pad flow in aluminum reduction cells[D]. Changsha:Central South University, 2002: 76−85.
[9] 吴建康, 黄 珉, 黄 俊, 姚世焕. 铝电解槽电解质−铝液流动及铝液表面变形计算[J]. 中国有色金属学报, 2003, 13(1):241−244.WU Jian-kang, HUANG Min, HUANG Jun, YAO Shi-huan.Computation of flow field of electrolyte-aluminium liquid and surface distortion of aluminum liquid in reduction cell[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(1): 241−244.
[10] LI Jie, LIU Wei, LAI Yan-qing, WANG Zhi-gang, LIU Ye-xiang.Analysis of cathode voltage drop in aluminum electrolysis cells with an electric contact model[C]//SØRLIE M. Light Metals.Orlando, FL: TMS, 2007: 465−470.
[11] LI Mao, ZHOU Jie-min. Modeling and optimization of busbar configuration in aluminum electrolysis cells with genetic algorithm[C]//HAGNI A M. Light Metals. Seattle, WA: TMS,2010: 489−492.
[12] PETERSON R D, RICHARDS N E, TABEREAUX A T. Results of 100-hour electrolysis test of a cermet anode: operational results and industry perspective [C]//BLCKERT C M. Light Metals. Warrendale, LA: TMS, 1990: 385−393.
[13] GEORGES B, NORA V D. Aluminum production cell and cathode. US, 6358393[P]. 2002−03−19.
[14] NORA V D. Cell for aluminum electrowinning. US 6093304[P].2000−07−25.
[15] 刘 伟, 李 劼, 赖延清. 铝电解槽电磁流场数学建模及应用[J]. 中国有色金属学报, 2008, 18(5): 909−916.LIU Wei, LI Jie, LAI Yan-qing. Development and application of electro-magneto-flow mathematic model of aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(5):909−916.
[16] LI Jie, LIU Wei, LAI Yan-qing, LIU Ye-xiang. An improved finite element model for electro-magnetic analysis in aluminum cells[J]. JOM, 2008, 60(2): 58−61.
[17] LI Jie, LIU Wei, LAI Yan-qing, LI Qin-yu, LIU Ye-xiang.Coupled simulation of 3D electro-magneto-flow field in hall-heroult cells using finite element method[J]. Acta Metallurgica Sinica: English Letters, 2006, 19(2): 105−116.
[18] 徐宇杰. 铝电解槽内熔体运动数学建模及应用研究[D]. 长沙:中南大学, 2010.XU Yu-jie. A study of mathematical modeling and its application for the melts motion in aluminium reduction cells[D]. Changsha:Central South University, 2010.
Simulation and optimization of bus structure and
electro-magneto-flow field of aluminum reduction cells with vertical bottom bars
LIU Ye-xiang1, LIANG Xue-min1,2, LI Jie1, ZHANG Hong-liang1, XU Yu-jie1, DING Feng-qi1, ZHOU Zhong1
(1. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;2. Henan Zhongfu Industrial Co., Ltd., Gongyi 451200, China)
Based on the target of reducing the horizontal current and vertical magnetic field strength, thereby improving the magnetohydrodynamic stability, a kind of aluminium reduction cell with vertical bottom was improved, in which the current flowed out of cathode vertically instead of horizontally. An electromagnetic simulated model of a 400 kA cell with this structure was developed by ANSYS software, and a bus bar scheme that can make the best electromagnetic field distribution was obtained after being optimized according to the computing result. Adopting this bus bar scheme, the maximum and average values of vertical magnetic flux density are 1.658 mT and 0.401 mT, respectively, which are far lower than those in traditional cells, and the MHD computation further proves that the above cell can operate stably under a small anode-cathode distance and has great potential in energy saving.
aluminium electrolysis; bus bar optimization; multi-physical field
TF821
A
1004-0609(2011)07-1688-08
国家“十一五”科技支撑计划资助项目(2009BAE85B00);国家自然科学基金资助项目(50874020)
2011-01-12;
2011-05-20
李 劼,教授,博士;电话:0731-88876454;E-mail:csulightmatels@126.com
(编辑 李艳红)

