基于滑模变结构的TCR控制系统数学建模及仿真
吕康飞
(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)
基于滑模变结构的TCR控制系统数学建模及仿真
吕康飞
(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)
为了方便分析与系统设计,将非线性的TCR型SVC控制系统进行线性化,建立了基于滑模变结构的控制系统模型,为了检验模型的准确性,并运用Matlab软件进行了仿真.
非线性; 建模; 仿真; 滑模变结构
0 引言
随着我国电网建设的发展,越来越多的柔性输配电设备得到了广泛的应用.诸如变频器、磁控电抗器、有源滤波器、静止无功补偿设备等.TCR型SVC作为电力系统当中一种重要的无功补偿装置,应用始于20世纪60年代,自从1967年SVC在英国研制成功以后,西德、美国、瑞士等许多国家也竞相研制,并在电力系统中推广和应用,国内1999年在国家电力公司的资助下中国电科院开始了“静止无功补偿器实用化技术的研究”,并于2002年推出了具备全数字化控制、光电触发、综合自动化等技术的TCR平台,在电弧炉的治理领域有成功运用的经验.但总体看来,国内在器件和调节器技术方面还相对落后,由于国产高压晶闸管的制造工艺与国外同类产品相比差距较大,晶闸管的耐压和导通一致性差,故不得已采用进口器件,导致产品成本相对较高[1-6].
同时由于电力电子装置本身的非线性,使得其在系统设计与分析时面临着诸多不便.因此有必要对TCR控制系统进行建模,而滑模变结构控制中对被控对象的模型误差、对象参数的变化以及外部干扰有极佳的不敏感性,系统一旦进入滑动模态,在一定条件下就对外界干扰及参数扰动具有不变性,从而具有比鲁棒性更加优越的完全自适应性.利用该方法对TCR建模可以更好的反映其特性.本文在分析TCR工作过程的基础上建立了基于滑模变结构的TCR控制系统数学模型.并将该模型在Matlab中进行了仿真.
1 数学建模
滑模变结构控制是变结构控制系统的一种控制策略.这种控制策略与其他控制策略的根本区别在于控制的不连续性.这种不连续性可以称之为“继电特性”或表述为“一种使控制系统结构随时间变化的开关特性”.这种控制特性迫使系统在一定条件下沿着某条状态轨迹作小幅度、高频率的上下运动,即所谓的“滑动模态”或“滑模”运动.我们可以根据实际需要来设计这种滑动模态.由于这种滑模运动与系统的参数及扰动无关,处于滑模运动的控制系统就具有很好的鲁棒性.
首先假设触发角与输出电流在足够短的段内是线性的,输入量是触发电路的指令电流I,输出量是TCR电流ITCR.TCR型SVC的控制系统数学模型的建立先要考虑晶闸管的死区时间Td.我们先以简单的单相两脉波TCR进行分析.在这种TCR中,每半个周期触发角只能变化一次,也就是说,晶闸管被触发导通以后,在此半周期中,该晶闸管触发角的任何变化将不会起作用[7].这意味着所需触发角信号α在每个周期中只要采样两次.因此采样频率不需要超过基频的2倍.如果α在正的电压峰值到来前发生变化,它可以由反并联晶闸管对中的正向晶闸管来瞬时实现.然而在最不利的情况下,当α的更新刚好发生在电压正向峰值之后,将会有半个周期的延迟,直到下个电压峰值到来前被采样到.这种由于晶闸管不能响应α在任意时刻变化而产生的延迟就称为晶闸管的死区时间.对一个2脉波TCR,死区时间是一个0到T/2的随机量,这里T是电压基波的周期.因而死区时间的平均值定为T/4.
将上述结论推广到6脉波TCR,可以看到α的采样频率只要等于6倍的基频就够了.采样时刻可以选在一个周波中与三相电压对应的6个峰值前一瞬间.这样与2脉波的TCR相似,晶闸管的平均死区时间定为T/6的一半,即一个周期的1/12的时间,对于我国50?Hz系统这个时间为1.67?ms.
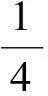

(1)
当α接近于90°时,上述时间常数为:
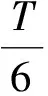
当α接近于180°时,上述时间常数为:
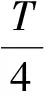
本文中所建数学模型时间常数取以下的的估计值:
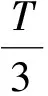
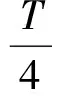

(2)
TCR数学模型参数推导结果如下:

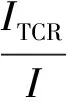
(3)
由于式(3)中包含指数函数e-Tds,它使系统成为非最小相位系统,分析和设计都比较麻烦.为了简化,先将e-Tds按泰勒级数展开,则式(3)变为:
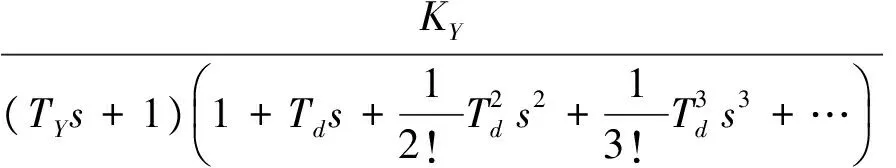
(4)
考虑到Td比较小,忽略其高次项,则I与ITCR的开环传递函数可近似成:

(5)
其中TY=5?ms,Td=1.67?ms,KY=1.

(6)
设计切换函数

(7)
其中,e=I-ITCR,c为系数.
采用指数趋近率
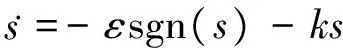
(8)
其中,ε>0,k>0,由(7)、(8)可得
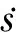
(9)
由(8)、(9)可得,

(10)
2 仿真验证
用Matlab进行控制系统仿真.指令电流为正弦信号,采用指数趋近律[10],趋近率参数ε=5,k=10.系统切换函数中系数c=5[11].正弦跟踪效果及控制系统特性如图1~图5所示.

图1 正弦跟踪结果

图2 正弦跟踪误差 图3 正弦跟踪相轨迹
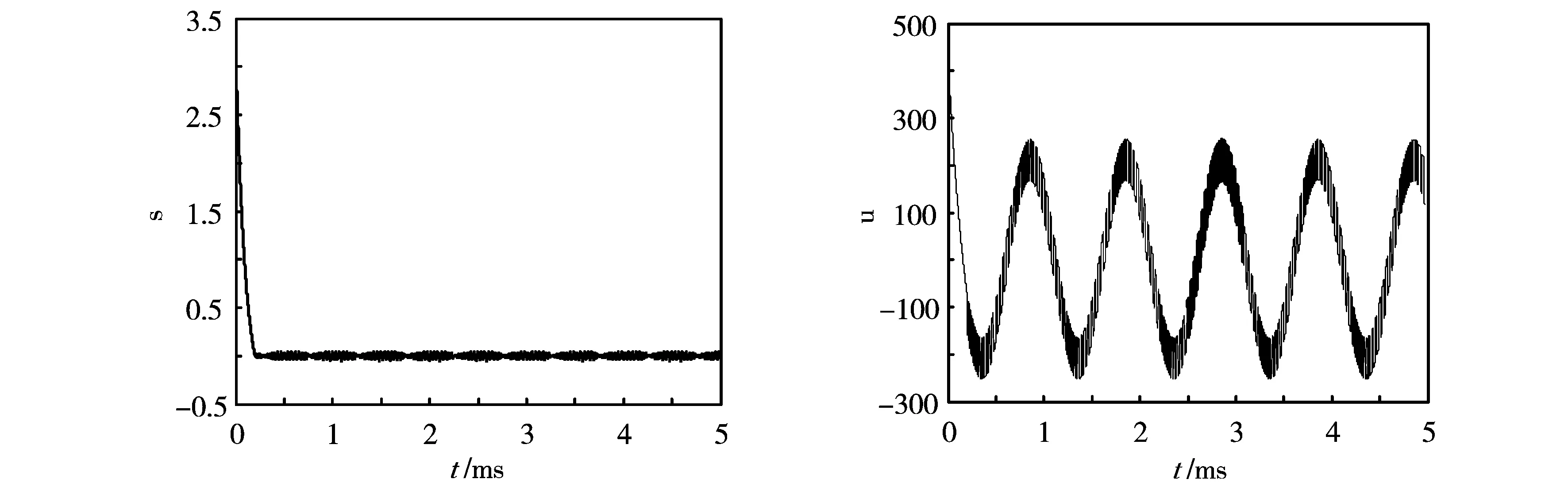
图4 切换函数变化特性 图5 控制率输出特性
图1~图5详细描绘了滑模控制系统的优良跟踪特性.从图4可以看出,经过大约0.2?ms,切换函数第一次过零点,控制系统运动点到达切换面,此后控制率u随着切换函数的正负而不断切换(如图5),约1?ms后,跟踪误差基本为零(如图2),此后指令电流和实际电流基本重合,正弦跟踪的效果非常完美.为了更加直观地描述控制系统的运动过程,绘制出控制系统相轨迹曲线(如图3),可以看到,当控制系统趋于稳态时,速度跟踪(即误差的导数)出现抖动,它被控制系统牢牢地吸引在斜率为-c的直线附近,选择不同的切换函数中参数c的值,可以对控制系统的动态品质进行调整.
3 结论
建立了TCR型SVC的数学模型,并在此基础上得到了基于滑模变结构的控制系统模型.通过Matlab仿真验证了该模型型在准确性和实时性上能很好的满足控制要求.
[1] 邓超. 一种TSC型SVC中晶闸管高频送能系统的研究?[J]. 电力电子技术,2011(3):55-59.
[2] 刘芳霞,孙霞. 煤矿电力系统中无功补偿的研究?[J]. 机械制造与自动化,2009(5):78-82.
[3] 孙晋超,刘凯. 基于MATLAB的电力系统稳定器和静止无功补偿器对电力传输稳定性的仿真?[J]. 电气开关,2008(1):22-26.
[4] 付康,龙军. 基于连续潮流法分析UPFC对电力系统潮流的控制?[J]. 电气开关, 2009(1):33-38.
[5] 傅旭,王锡凡,杜正春. 电力系统电压稳定性研究现状及其展望?[J]. 电力自动化设备, 2005(2):66-69.
[6] 朱方,赵红光,刘增煌,等. 大区电网互联对电力系统动态稳定性的影响?[J]. 中国电机工程学报, 2007,22(1):50-55.
[7] Mohan R, Mathur R, Varma K. Thyristor-based fscts controllers for electrical transmission systems?[M]. Newyork: John Wiley&Sons,1999.
[8] Liu H. Smooth sliding mode control of uncertain systems based on a prediction error?[J]. International journal of robust and nonlinear control,1997,7(4):353-372.
[9] Ma H, Zhang T. Sliding mode control for AC signal power amplifier?[J]. Proc of IEEE IECONO S,2005,10:12-17.
[10] Golo G,Milosavljevic C. Robust Discrete-Time Chattering Sliding Mode Control?[J]. Systems & Control Letters,2000,41(1):19-28.
[11] 李卫国, 陈洁, 徐双, 等. 基于结构保留模型的SVC非线性最优控制器设计?[J]. 东北电力大学学报, 2011,30(1):44-48..
[责任编辑:蒋海龙]
ModelingandSimulationforTCRControlSystemBasedonSlidingModeVariableStructureControl
LU Kang-fei
(School of Physics and Electronics Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)
In order to facilitate analysis and system design,make the nonlinear TCR type SVC control system linearization,modeling TCR control system based on sliding mode variable structure control.For verify the model,make use of Matlab for simulink.
nonlinear; modeling; simulink; sliding mode variable structure
TM76
A
1671-6876(2011)04-0312-04
2010-12-08
吕康飞(1980-), 男, 江苏徐州人, 助教, 硕士, 研究方向为电力电子、数字式变电站.

