OpenMP并行算法在卫星重力场模型反演中的应用*

周 浩 钟 波 罗志才 张 坤

(1)武汉大学测绘学院，武汉 430079

2)地球空间环境与大地测量教育部重点实验室，武汉430079)

OpenMP并行算法在卫星重力场模型反演中的应用*

周 浩1)钟 波1，2)罗志才1，2)张 坤1)

(1)武汉大学测绘学院，武汉 430079

2)地球空间环境与大地测量教育部重点实验室，武汉430079)

利用卫星重力数据反演地球重力场需要解决重力场模型的高效计算问题。分析了最小二乘直接法求解重力场模型涉及的密集型计算任务，基于OpenMP实现了卫星重力场模型直接求解的并行算法。利用30天、5秒采样间隔的沿轨扰动位T和径向扰动重力梯度Trr数据，分别反演了60阶次的卫星重力场模型，计算结果表明，OpenMP并行算法能够有效提高直接法求解卫星重力场模型的计算效率，并具有很好的稳定性。

并行算法;重力场模型;卫星重力;重力梯度;OpenMP

1 引言

卫星重力测量技术为解决全球高覆盖率、高空间分辨率和高时间重复率的重力测量开辟了新途径，特别是新一代卫星重力计划的成功实施，已使得地球重力场模型的中长波部分精度提高了约2个量级［1-3］。

新一代卫星重力测量数据具有高采样率、全球观测的特点。利用卫星重力观测值反演地球重力场将面临海量数据的处理问题，特别是对于高阶重力场模型的反演，其计算量巨大，计算过程极为耗时。为了利用海量卫星重力观测值快速求解高精度的地球重力场模型，许多学者一方面是对现有重力场恢复方法进行改进，提出了一些快速解算法［4-6］;另一方面就是采用并行算法，即基于并行计算机，编写合适的并行算法来提高计算速度［7-9］。本文对最小二乘直接求解过程中的密集型计算任务进行了分析，并基于OpenMP实现其并行求解，最后通过数值计算对其有效性进行了分析与验证。

2 重力场求解的并行算法［9－14］

重力场最小二乘直接求解的并行算法的计算步骤如图1所示。从图1可以看出，构建设计矩阵A、构建法方程系数阵N和b，以及解算法方程3个部分为计算的“热点”，应该引入并行算法进行优化。下面将基于OpenMP实现各个计算“热点”的并行。

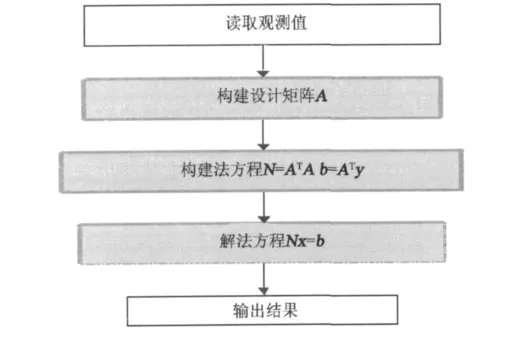
图1 直接解法计算流程图Fig.1 Flow chart of the computation with direct method

2.1 构建设计矩阵A的并行

由于设计矩阵A的行与行之间无相关性，且每行的构建具有相似性，为此，程序中使用BUILD_A_ THREAD子函数来构建矩阵A中的一行，然后根据OpenMP语法需求，加入组合并行共享任务制导语句!$OMP PARALLEL DO/!$OMP END PARALLEL DO实现构建设计矩阵A的并行。具体形式为：

!$OMP PARALLEL DO

DO I=1，NOBS

CALL BUILD_A_THREAD(……)

END DO

!$OMP END PARALLEL DO

其中，NOBS为观测值个数，即设计矩阵A的行数。

2.2 矩阵相乘的并行

由图1可知，根据最小二乘构建法方程包含两个矩阵相乘运算，均是计算的“热点”，有必要实现矩阵相乘的并行，以加速构建法方程。构建法方程可用直接法、分块法、斯特拉森法等矩阵相乘的并行算法。

1)直接法

设矩阵A=(aij)为m×n矩阵，矩阵B=(bij)为n×l矩阵，其乘积C=AB=(cij)为m×l矩阵，其中：

式(1)各次计算中都要用到i、j、k，所以在并行过程中，需要各个节点都有一份这些参量的拷贝。根据OpenMP语法需求，需要将i、j、k设置为PRIVATE属性，同时使用并行共享任务制导语句! $OMP PARALLEL DO/!$OMP END PARALLEL DO实现并行。具体形式为：

!$OMP PARALLEL

!$OMP DO PRIVATE(i，j，k)

DO i=1，M

DO j=1，L

C(i，j)=0.0

DO k=1，N

C(i，j)=C(i，j)+A(i，k)*B(k，j)

END DO

END DO

END DO

!$OMP END DO

!$OMP END PARALLEL

2)分块法

行列分块法的具体计算过程是首先将矩阵A、B、C分解为：

然后由A、B阵中的分块相乘得到C阵中的对应分块，例如C11=A11B11+A12B21。至于分块矩阵乘法的并行，其处理方式与直接法相同。

3)斯特拉森(Strassen)算法

利用此种方法主要是为了减少矩阵乘法中的运算量，降低时间复杂度。与分块法一样，首先按照式(2)将矩阵A、B、C进行行列分解，然后引入中间变量：

利用中间变量相加得到最后结果：

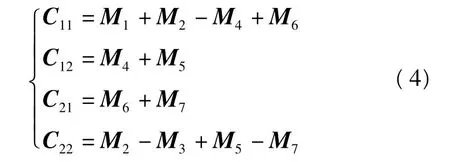
斯特拉森算法的实质是反复使用二阶矩阵乘法，使计算复杂度从O(n3)降为O(n2.81)。为了保证在M阵计算完成以后才计算C阵，可以引入隐含并行同步语句!$OMP BARRIER，具体形式为：

!$OMP PARALLEL

!$OMP DO PRIVATE(i，j，k)

实现公式(3)

!$OMP END DO

!$OMP BARRIER

!$OMP DO PRIVATE(i，j，k)

实现公式(4)

!$OMP END DO

!$OMP END PARALLEL

2.3 求解法方程的并行算法

根据计算流程，得到法方程中各个矩阵后，则可对法方程进行求解。并用直接法、平方根法和改进的平方根法实现相应的OpenMP并行算法。

1)直接法

直接法分为矩阵求逆和矩阵相乘。其中，采用高斯-约当方法对矩阵求逆。由于高斯-约当法求逆是按照行序i进行的，故按照下面方式实现并行：

DO i=1，U

处理对角线元素

!$OMP PARALLEL SHARED(N，i)

!$OMP DO PRIVATE(j)

!$OMP FLUSH(N)

处理主行元素

!$OMP END DO

!$OMP BARRIER

!$OMP DO PRIVATE(j，k)

!$OMP FLUSH(N)

处理非主行非主列元素

!$OMP END DO

!$OMP BARRIER

!$OMP DO PRIVATE(k)

!$OMP FLUSH(N)

处理主列元素

!$OMP END DO

!$OMP BARRIER

!$OMP END PARALLEL

END DO

其中，U为法方程系数阵N的维数。加入!$OMP FLUSH和!$OMP BARRIER语句，是为了保证数据的实时刷新与严格同步［13］。

2)平方根法［15］

由于法方程系数阵N=ATA为对称正定阵，故可以利用平方根法求解法方程。法方程系数阵N可以作乔列斯基(Cholesky)分解，如果设定一次乘法和加法运算时间或一次除法运算时间为一个单位时间，则采用平方根方法的计算时间为(n3+3n2+ 2n)/6，计算整个方程的时间为(n3+9n2+2n)/6。

3)改进的平方根法

!$OMP PARALLEL DO SHARED(N，j)num_ threads(U-j-1)

DO j=1，U

!$OMP PARALLEL DO SHARED(N，p，j) num_threads(U-j-1)

DO p=j+1，U

DO q=j+1，p

N(p，q)=N(p，q)-N(p，j)*N(q，j)/N(j，j)

END DO

END DO

!$OMP PARALLEL DO SHARED(N，j)

DO i=j+1，U

N(i，j)=N(i，j)/N(j，j)

END DO

END DO

利用上述代码实现N阵的分解后，利用简单的矩阵乘法即可获得法方程的解。

3 算例与分析

计算采用Dell R900共享内存并行计算机，处理器为4颗4核的Intel E7430，主频2.13GHz，内存64GB，编译环境为Intel Visual Fortran 10.1。基于GOCE卫星模拟轨道数据，采用60阶次的EIGENGL04C模型分别模拟了沿轨30天、5秒采样间隔(总共518 400个观测数据)的扰动位T和径向扰动重力梯度Tzz数据，并进行重力场反演和精度比较分析。

3.1 设计矩阵计算与分析

首先设定不同的线程数来构建设计矩阵A(维数为518 400×3 721)。以Tzz数据计算为例，获得计算所需时间如表1所示。

表1 构建设计矩阵A的时间分析(单位：s)Tab.1 Runtime of building design matrix A(unit：s)

表1中，“加速比”是指在相同任务量下的并行执行时间与串行执行时间之比。若加速比与线程数的比例能够接近于1，则表明该算法能够达到线性加速比，并行效率高［9，14］。由表1中第1～3列可知，对构建设计矩阵A的并行基本上可达到线性加速比，由此可知构建设计矩阵A的并行计算效率较高;而第4列和第5列之所以未能够达到线性加速比，是因为本文采用的数据量较小，导致有些线程还没有参与计算就已结束了计算任务。

3.2 矩阵乘法的计算与分析

设定不同的线程数，采用直接法、分块法和Strassen法分别实现矩阵乘法的并行计算，数据计算结果如图2所示。

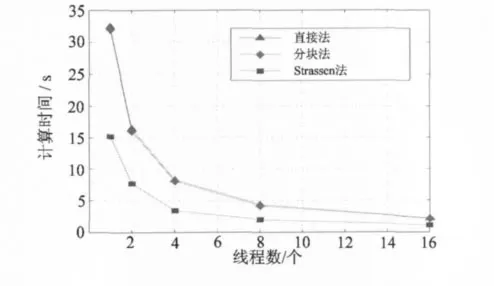
图2 不同矩阵相乘的并行计算效率比较Fig.2 Comparison among the efficiency of parallel methods for matrix multiplication

在评价并行算法时，我们通常假定任务量W一定，若随着线程数p的增加，计算所需时间t缩短，且近似满足t=W/p，则该并行算法是成功的。由图2可知，3种方法的并行效率都趋近于反比例函数，这说明3种矩阵乘法的并行算法均是成功的。

从图2还可知：在相同线程数、相同任务量的前提下，分块法计算时间略小于直接法，而Strassen法的计算时间则最小。

3.3 法方程解算与分析

采用直接法、平方根法和改进的平方根法，使用不同阶数的法方程阵，分别实现了法方程求解的并行算法(计算中设定12个线程数)，计算结果如图3所示。

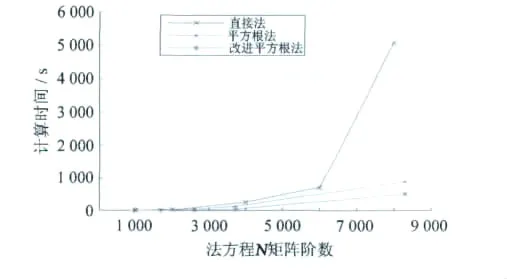
图3 不同求解法方程方法的并行效率比较Fig.3 Comparison among the parallel efficiency of different methods for solving the normal equation

从图3可以看出：在相同线程数的前提下，随着任务量的增加，计算所需时间迅速增加;在解算所需时间上，改进的平方根法相比于直接法和平方根法具有极大的优势，这说明改进的平方根法的时间复杂度最小。但为了获得更高精度的解算结果和精度评定的参数协因数阵，本文选用直接法对法方程进行求解。

3.4 重力场反演计算与分析

分别采用518 400个观测历元的扰动位T和二阶径向扰动重力梯度Tzz数据来反演60阶次的地球重力场模型，其中3个计算“热点”分别使用构建设计矩阵的并行算法、Strassen矩阵相乘的并行算法、直接法求解法方程的并行算法，计算时间如表2所示。

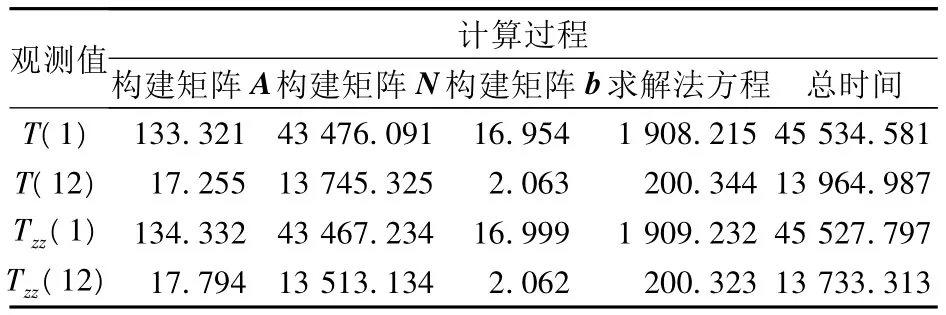
表2 反演卫星重力场模型计算时间表(单位：s)Tab.2 Computational runtime of gravity model inversion (unit：s)

从表2可知，在本文计算条件下，使用串行算法利用一个月的观测数据反演60阶的重力场模型，约需要12小时，当采用12个线程的OpenMP计算时，计算时间可节约8个小时。若使用更长时间跨度的观测数据，理论上节省的计算时间将更长。

采用模型阶误差RMS分别对扰动位T和二阶径向扰动重力梯度Tzz数据反演的重力场模型精度进行评价：

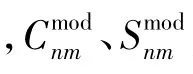
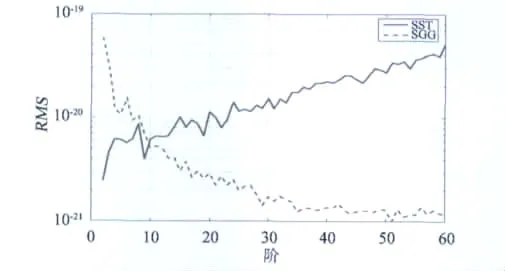
图4 利用T和Tzz求解模型的阶误差RMSFig.4 Degree error RMS of different models for solving the T and Tzz

4 结束语

基于OpenMP实现了由最小二乘直接法求解卫星重力场模型的并行算法。通过数值计算分析表明：采用按行存储方式实现的构建设计矩阵的并行算法，基本可达到线性加速比;采用Strassen法实现的矩阵乘法并行计算能够减小计算的复杂度，极大提高计算效率;采用直接解法求解法方程的并行算法能提高计算效率，并可保证求解结果的准确性和可靠性。因此，基于OpenMP的并行算法是反演地球重力场模型的有效工具。由于OpenMP是基于共享存储系统上的并行编程标准，系统开销较大，将在后续工作中利用OpenMP与MPI的联合编程，实现更长时间序列数据反演超高阶次地球重力场的并行运算。

1 宁津生.卫星重力探测技术与地球重力场研究［J］.大地测量与地球动力学，2002，(1)：1-5.(Ning Jinsheng.The satellite gravity surveying technology and research of Earth’s gravity field［J］.Journal of Geodesy and Geodynamics，2002，(1)：1-5)

2 许厚泽.卫星重力研究：21世纪大地测量研究的新热点［J］.测绘科学，2001，26(3)：1-3.(Xu Houze.Satellite gravity mission-new hot point in Geodesy［J］.Science of Surveying and Mapping，2001，26(3)：1-3)

3 孙文科.低轨道人造卫星(CHAMP、GRACE、GOCE)与高精度地球重力场——卫星重力大地测量的最新发展及其对地球科学的重大影响［J］.大地测量与地球动力学，2002，(1)：92-100.(Sun Wenke.Satellite in low orbit (CHAMP，GRACE，GOCE)and high precision Earth gravity field：the latest progress of satellite gravity geodesy and its great influence on geosciences［J］.Journal of Geodesy and Geodynamics，2002，(1)：92-100)

4 Sanso F and Tscherning C C.Fast spherical collocation：theory and examples［J］.Journal of Geodesy，2003，77：101 -112.

5 Klees R，et al.Efficient gravity field recovery from GOCE gravity gradient observations［J］.Journal of Geodesy，2000，74：561-571.

6 Sneeuw N.A semi-analytical approach to gravity field analysisfrom satellite observations［D］.University of München，2000.

7 Klees R，et al.GOCE gravity field recovery using massive parallel computing［A］.Gravity，Geoid and Geodynamics 2000［C］.F Sansò(eds.)：IAG symposium，2002，123：109-116.

8 Pail R and Plank G.Assessment of three numerical solution strategies for gravity field recovery from GOCE satellite gravity gradiometry implemented on a parallel platform［J］.Journal of Geodesy，2002，76：462-474.

9 Wittwer T.An introduction to parallel programming［M/ OL］.http：//www.vssd.nl/hlf/a019.htm.

10 罗志才.利用卫星重力梯度数据确定地球重力场的理论和方法［D］.武汉测绘科技大学，1996.(Luo Zhicai.The theory and methodology for determining the earth’s gravity field using satellite gravity gradiometry data［D］.Wuhan Technical University of Surveing and Mapping，1996)

11 王正涛.卫星跟踪卫星测量确定地球重力场的理论与方法［D］.武汉大学，2005.(Wang Zhengtao.Theory and methodology of earth gravity field recovery by satellite-tosatellite tracking data［D］.Wuhan University，2005)

12 钟波.基于GOCE卫星重力测量技术确定地球重力场的研究［D］.武汉大学，2010.(Zhong Bo.Study on the determination of the earth’s gravity field from satellite gravimetry mission GOCE［D］.Wuhan University，2010)

13 Hermanns M.Parallel programming in Fortran 95 using OpenMP［M/OL］.http：//www.openmp.org/presentations/miguel/F95_OpenMPv1_v2.pdf.

14 陈国良，等.并行算法实践［M］.北京：高等教育出版社，2004.(Chen Guoliang，et al.Parallel algorithm practice［M］.Beijing：Higher Education Press，2004)

15 朱方生，李大美，李素贞.计算方法［M］.武汉：武汉大学出版社，2003.(Zhu Fangsheng，Li Damei and Li Shuzhen.Numerical method［M］.Wuhan：Wuhan University Press，2003)

APPLICATION OF PARALLEL ALGORITHMS BASED ON OpenMP TO SATELLITE GRAVITY FIELD RECOVERY

Zhou Hao1)，Zhong Bo1，2)，Luo Zhicai1，2)and Zhang Kun1)

(1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079 2)Key Lab.of Geospace Environment and Geodesy，Ministry of Education，Wuhan University，Wuhan 430079)

The massive satellite data presents a significant computational challenge to estimate the gravity field.Analyzing the computing-intensive tasks in recovering the earth gravity field model based on the direct leastsquares algorithms，on applying parallel computing techniques capable of rigorously inverting geopotential coefficients using direct method on the basis of OpenMP is focused.Eventually，the earth’s gravity fields complete to degree and order 60 are recovered respectively on the basis of monthly along track disturbing potential observations and gravity gradient observations(with 5 s sampling interval).The simulation shows that introducing the parallel algorithms based on OpenMP into determination of the earth’s gravity field model can be more effective，and is of great reliability.

parallel algorithms;gravity filed model;satellite gravimetry;gravity gradient;OpenMP

1671-5942(2011)05-0123-05

2011-06-17

国家自然科学基金(40874002，41104014);国家863计划项目(2008AA12Z105);测绘遥感信息工程国家重点实验室专项科研经费资助项目(2009);地球空间坏境与大地测量教育部重点实验室开放基金(10-02-09)

周浩，男，1987年生，硕士研究生，主要从事卫星重力学研究.E-mail：lengyeshanren@126.com

P223，P228

A