基于整体最小二乘的稳健点云数据平面拟合*

官云兰 刘绍堂 周世健 张立亭 鲁铁定

(1)东华理工大学测绘工程学院，抚州 344000 2)河南工程学院土木工程系，郑州 451191 3)江西省科学院，南昌330029)

基于整体最小二乘的稳健点云数据平面拟合*

官云兰1)刘绍堂2)周世健1，3)张立亭1)鲁铁定1)

(1)东华理工大学测绘工程学院，抚州 344000 2)河南工程学院土木工程系，郑州 451191 3)江西省科学院，南昌330029)

针对点云数据平面拟合方法没有完整考虑测量数据中的误差及系数阵中误差的情况，提出稳健整体最小二乘点云数据平面拟合方法。该法以整体最小二乘法为基础，在考虑全部观测量存在误差的情况下，通过一定的准则删除数据中的粗差或异常值，从而获得稳健的平面参数估值。实验中，分别利用最小二乘法、特征值法和稳健整体最小二乘拟合法对仿真点云数据和真实点云数据进行平面拟合，结果显示该法能克服异常值的影响，得到可靠的平面参数估值，具有稳健性。

点云数据;整体最小二乘;平面拟合;异常值;稳健性

1 引言

地面三维激光扫描是一种新型的空间数据获取技术，利用它可以对实物进行数字化，快速获取物体表面大量点的三维坐标，称为点云数据，从而迅速描绘和量化复杂环境。该技术为快速获取空间数据提供了有效手段［1］。利用点云数据进行建模也成为许多3D建模研究人员关注的问题之一。

平面拟合是地面三维激光扫描数据处理中的常用步骤之一，通过平面拟合不仅可以实现平面标靶的定位，从而完成基于平面标靶的多视点云数据配准，也可以实现对真实场景中平面特征的建模。众多学者［2-5］对从点云数据中提取平面特征进行了研究，包括最小二乘法、特征值法等。最小二乘法在假设x、y为独立变量，不含误差，而z为依赖变量，包含误差的情况下解算平面参数，但由于点云数据获取时x、y、z 3个方向均存在误差，因此严格来说最小二乘法并不适合于点云数据平面拟合的解算;特征值法是在满足条件a2+b2+c2=1情况下，根据平面方程ax+bY+cz=d计算平面参数，这种方法仅根据x、y、z 3个方向误差的整体组合解算平面参数，并未单独考虑各方向的误差影响。文献［5］在特征值算法的基础上，以最小二乘法为原则，提出了稳健的平面拟合算法。本文则在考虑点云数据在x、y、z 3个方向上均有误差、同时数据中存在粗差或异常值的情况下，提出基于整体最小二乘的稳健点云数据平面拟合算法。

2 整体最小二乘平面拟合

设空间平面方程为

其中a、b、c为待估参数。

设对某一平面进行扫描，得到n个扫描点坐标{(xi，yi，zi)，i=1，2，…，n}。考虑到数据在x、y、z 3个方向均存在误差，则方程改为：

其中vx、vy、vz分别为x、y、z 3个方向的误差改正数。

将上式整理，可得

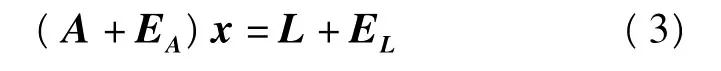
式中EA、EL分别表示矩阵A和向量L的误差，即

通常采用矩阵奇异值分解(SVD)解算待定参数的整体最小二乘解［6-8］。

其中

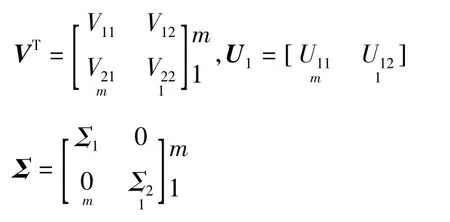
则参数的整体最小二乘估值为：

残差矩阵为：

单位权中误差为：

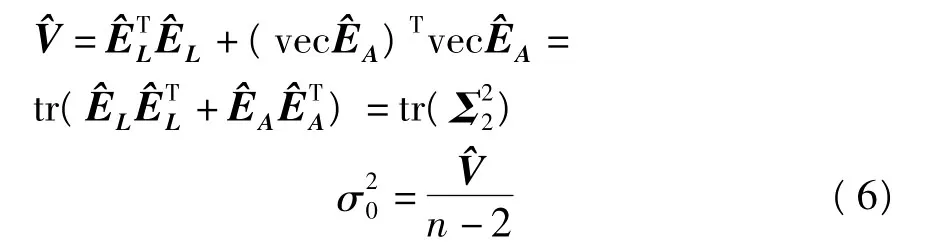
也可以采用如下公式进行计算［9］：

其中σ3为增广矩阵［A L］的最小特征值。

3 异常点的删除

在利用地面激光扫描系统对研究对象进行扫描时，由于各种因素影响，如扫描时行人通过、树木遮挡等，必然使得获取的点云数据存在异常点。因此为了提高拟合精度，在采用整体最小二乘法解算时，还需要去除点云数据中的异常点，以获取稳健的平面参数a、b、c的估计值。具体算法如下：

1)利用整体最小二乘法计算a、b、c的初始值;

2)根据计算出的a、b、c值，采用

计算每个点至拟合平面的距离di;

3)利用

计算距离di的标准偏差。其中：

4)当di＞2σ时，此点被认为是异常点，删除;反之，保留;

5)利用所有保留下来的点通过整体最小二乘重新计算参数a、b、c，即可获得最佳平面参数。

4 实验及结果分析

为了验证本算法的可靠性和稳健性，首先采用仿真数据进行实验。设要拟合的空间平面方程为

利用Matlab［10］从此平面上随机抽取1 000个点(图1)，并通过Matlab编程，利用最小二乘法、特征值法及稳健整体最小二乘法对上述仿真数据进行参数估计，表1为计算结果。

当数据中存在异常值时(人为地使其中的8个点成为异常点(图2，小圈圈出的表示异常点))的计算结果如表2所示。

通过表1、2可以看出：当数据不存在异常值时，3种方法计算结果基本一致，本文方法精度最高;当数据中存在异常值时，本文方法最准确且精度最高。

图1 模拟平面点云数据Fig.1 Simulated plane point clouds

表1 模拟平面参数的设定值及各种方法的参数估值(不含异常值的结果)Tab.1 Parameters of simulated plane and its estimated values(without outliers)

图2 具有异常点的模拟平面点云数据Fig.2 Simulated plane point clouds with outliers

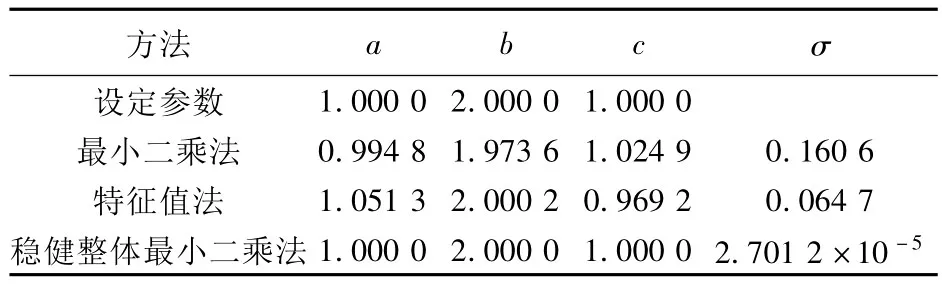
表2 模拟平面参数的设定值及各种方法参数估值(人为加入异常值后的结果)Tab.2 Parameters of simulated plane model and its estimated values(with outliers)

为了进一步说明本文算法的准确性，采用真实点云数据进行计算。该数据为在距离一平面标靶10m处对其进行扫描，扫描结果见图3。

由图3可知数据中存在大量的非标靶平面上的点。现利用最小二乘法、特征值法及稳健整体最小二乘法估计标靶的参数，结果见表3。

为了验证平面参数的正确性，现根据计算出的空间平面参数，计算扫描仪到该平面标靶的距离，结果见表4。

由表4可知，根据稳健整体最小二乘法计算出的结果最接近真实的距离，由此可见，本文方法的计算结果比其他方法所得结果更可靠。

图3 平面标靶及其点云数据Fig.3 Plane target and its point cloud data

表3 各种方法得到的空间平面参数值Tab.3 Estimated parameters for real plane target obtained with various methods

表4 扫描仪到标靶的平面距离(单位：m)Tab.4 Estimated distances between the real target and scanner(unit：m)

5 总结

真实场景中存在大量的平面特征，利用地面三维激光扫描仪对其进行扫描时，获取的数据中不可避免地存在误差及异常值。本文在整体最小二乘的基础上，提出了一种稳健平面拟合方法，并通过实验与传统方法进行比较，结果证明了该算法的稳健性和可靠性。该方法不仅适用于从点云数据中拟合平面，也适用于其他包含异常值的数据的平面拟合。

需要说明的是，在进行拟合前，需要对点云数据进行分割，将可能相同特性的点划分为同一集合再进行拟合。

1 罗德安，等.基于3维激光影像扫描技术的整体变形监测［J］.测绘通报，2005，(7)：40-42.(Luo Dean，et al.Whole object deformation monitoring based on 3D laser scanning technology［J］.Bulletin of Surveying and Mapping， 2005，(7)：40-42)

2 Prabhat K Acharya，et al.Parameter estimation and error analysis of range data［B/OL］.http：//ieee-xplore.ieee.org/xpls/abs_all.jsp?arnumber=12312，2002.8.

3 何文峰，查红彬.基于平面特征的深度图像配准［A］.中国人工智能进展［C］.北京：北京邮电大学出版社，2003.(He Wenfeng and Zha Hongbing.Registration of range data based on planar features［A］.Advance in artificial intelligence in China［C］.Beijing：Beijing University of Posts and Telecommunications Press，2003)

4 Wang Caihua，et.al.Comparison of local plane fitting methods for range data［B/OL］.http：//ieeexplore.ieee.org/ xpls/abs_all.jsp?arnumber=990538，2003.4.

5 官云兰，等.一种稳健的点云数据平面拟合方法［J］.同济大学学报(自然科学版)，2008，36(7)：981-984.(Guan Yunlan，et al.A robust method for fitting a plane to point clouds［J］.Journal of Tongji University(Natural Science)，2008，36(7)：981-984)

6 Golub G H and Lan Loan F C.An analysis of the total least squares problem［J］.SIAM Journal on Numerical Analysis，1980，17(6)：883-893.

7 Burkhard Schaffrin.A note on constrained total least squares estimation［J］.Linear Algebra and its Application，2006，(417)：245-258.

8 鲁铁定，等.基于整体最小二乘的地面激光扫描标靶球定位方法［J］.大地测量与地球动力学，2009，(4)：102-105.(Lu Tieding，et al.Sphere target fixing of point cloud data based on TLS［J］.Journal of Geodesy and Geodynamics，2009，29(4)：102-105)

9 张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2008.(Zhang Xianda.Matrix analysis and applications［M］.Beijing：Tsinghua University Press，2008)

10 龚剑，朱亮.Matlab 5.X入门与提高［M］.北京：清华大学出版社，2000.(Gong Jian and Zhu Liang.Matlab 5.X introduction and improvement［M］.Beijing：Tsinghua University Press，2000)

ROBUST PLANE FITTING OF POINT CLOUDS BASED ON TLS

Guan Yunlan1)，Liu Shaotang2)，Zhou Shijian1，3)，Zhang Liting1)and Lu Tieding1)

(1)School of Surveying and Mapping Engineering，East China Institute of Technology，Fuzhou 344000 2)Department of Civil Engineering，Henan Institute of Engineering，Zhengzhou 451191 3)Jiangxi Academy of Science，Nanchang330029)

In traditional plane fitting methods for point clouds，people don’t consider errors in data and in coefficients matrix simultaneously，which will result in incorrectness of plane parameters.In order to overcome this shortcoming，a new method for fitting local plane to point clouds was proposed.The method is based on total least squares.In consideration of the errors in all observation data，we tried to delete outliers from point clouds，and thus obtained a robust solution to plane fitting parameter.Analytical experiments based on simulated data and real data were conducted，and comparisons between the method and traditional methods such as least square method and eigenvalue method were also implemented.The results show that the method has the capability to overcome bad influence from outliers，and to increase the reliability of parameters estimation.

point clouds;Total Least Squares(TLS);plane fitting;outliers;robustness

1671-5942(2011)05-0080-04

2011-05-17

国家自然科学基金(40874010);江西省自然科学基金(2008GQC0001，2010GZC0009，2010GZC0008);地球空间环境与大地测量教育部重点实验室开放基金(10-01-06)

官云兰，女，1975年生，副教授，博士，主要从事摄影测量与遥感、GIS的教学与科研工作.E-mail：guan8098@163.com

P207

A