加权最小二乘相位解缠的一种改进*

董春敏 刘国林 于胜文 刘伟科 周 伟

(1)山东科技大学测绘科学与工程学院，青岛 266510 2)海岛(礁)测绘技术国家测绘局重点实验室，青岛266510)

加权最小二乘相位解缠的一种改进*

董春敏1)刘国林1，2)于胜文1)刘伟科1)周 伟1)

(1)山东科技大学测绘科学与工程学院，青岛 266510 2)海岛(礁)测绘技术国家测绘局重点实验室，青岛266510)

基于最小二乘相位解缠原理，针对现有的加权和不加权最小二乘在残差点过多时计算结果平滑问题，提出利用相位导数变化图对其进行加权改进。结合真实数据，通过现有的加权与不加权最小二乘算法的比较和分析，证明该改进算法能有效处理残差点过多的情况，解缠精度高，解缠结果更可靠。

InSAR;相位解缠;加权最小二乘;相位导数变化;残差

1 前言

InSAR技术的应用已经涉及到很多领域，如地形测量、冰川研究、森林调查与制图、海洋研究、获取战略、战术机动和定期威胁军事目标等。而相位解缠是利用InSAR技术获取高精度目标高程信息的关键步骤，展开后的InSAR相位差直接关系到DEM信息提取的准确性和精确性。

近20年来，InSAR二维相位解缠算法研究发展十分迅速，它们大致可以分为3类。第一类是基于路径跟踪的算法［1］，主要有：Goldstein枝切法、质量图指导算法、掩膜切割(Mask-cut)算法、Flynn最小不连续法等;第二类是基于最小范数的算法，主要有：不加权的最小二乘算法［2］、预解共轭梯度(PCG)算法、加权多网格算法、最小Lp范数算法［1］等;第三类是基于最优估计的算法，主要有：基于网络规划的算法［3］、卡尔曼滤波法［4］、基于贝叶斯估计的方法［5］、遗传算法［6］等。

Goldstein枝切法运算速度快，效率高，占用内存小，对噪声小的区域能够得到正确的解缠结果，但是对于含有大量不连续点的区域，由于不能设置正确的枝切线，解缠结果误差大［7］;质量图指导法对相位质量图要求高，只有具备可靠的质量图，解缠才能成功的进行;由于质量掩膜会造成一些孤立区域，Mask-cut算法适合于残差点仅分布于低质量相位区的情况;Flynn最小不连续法和基于网络规划的算法适应性强，解缠结果较可靠，但是它们各自的算法复杂，所以耗费的时间较长;最小Lp范数算法解缠稳定性较好，不需要识别残差点，但是它们是“穿过”而不是“绕过”残差点，解缠的同时会导致误差向高质量区域传递。

本文在对最小二乘相位解缠算法研究基础上，针对现有的最小二乘算法在残差点过多时计算结果平滑问题，提出利用相位导数变化图对其进行加权改进，利用MATLAB对新算法进行了实现，结合真实数据，借助原有加权最小二乘解缠算法，从目视和定量两个方面对3种解缠算法进行了分析和比较。验证了新算法的有效性。

2 最小二乘相位解缠

InSAR测量技术是利用从雷达复图像数据中衍生出的相位信息提取地表三维信息。它的基本原理是通过两部天线同时观测，或者两次平行的观测，获取地面上同一地物的两幅复雷达图像，利用两幅复图像相关运算得到的相位差反演地物的相对高程。但是实际上这样得到的干涉相位差是真实相位差的卷叠，即InSAR干涉图中与地面位置直接相关的相位是以2π为模的，所以为了计算每一点的高程必须给每一个相位测量值加上整数倍的相位周期，这种求解2π模糊性问题的技术称为相位解缠。

对于缠绕相位函数Ψi，j(i=0，1，2，…，M-1;j =0，1，2，…，N-1)对应的解缠相位函数φi，j，则最小LP范数解必须满足［1］

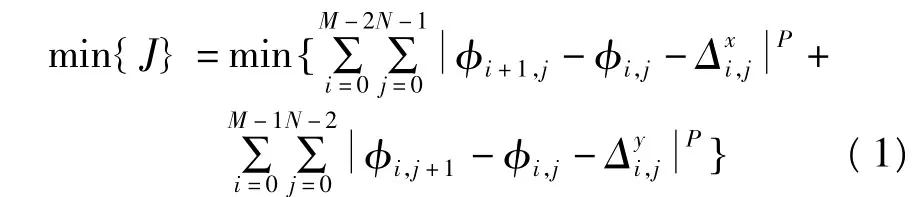
其中，

记

令δJ=0，将i，j互换，得到

对于边界满足ai，j=bi，j=0，那么有

假设扰动δφi，j是随机的，则应有

求解式(10)，需要知道φ-1，j，φM，j，φi，-1，φi，N及对应的φ-1，j，φM，j，φi，-1，φi，N值，根据边界条件有：

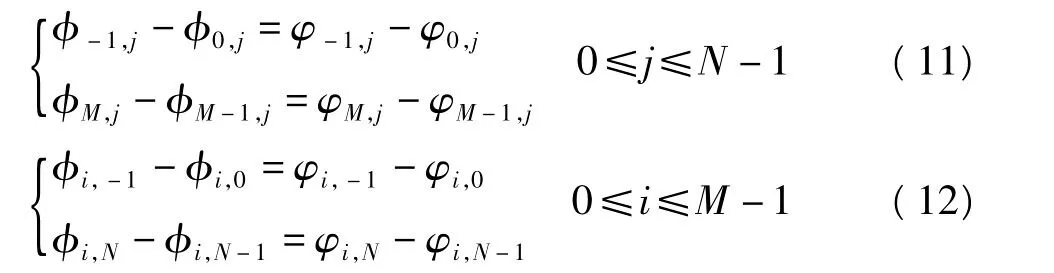
展开式(10)，并加上边界条件，有：

当p=2，式(13)为离散形式的泊松方程

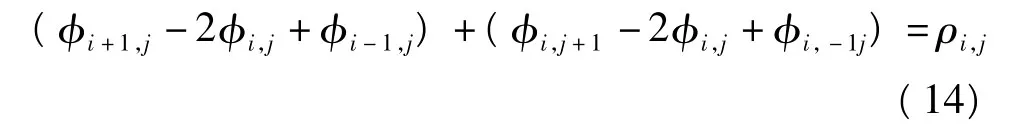
其中，

由分析可以看出，当p=2时，最小Lp范数的相位解缠问题等效于求解纽曼边界的泊松方程，而此时的最小Lp范数算法也就是一般意义下的最小二乘相位解缠算法，它的目标是使缠绕相位Ψi，j与解缠相位φi，j的梯度差的平方和最小。最小二乘算法可以采用基于FFT或DCT的方法来加快算法的解缠速度。

基于FFT的最小二乘算法的具体实施步骤如下［8］：

1)计算0≤i≤M，0≤j≤N时的ρi，j值。

2)计算ρi，j的傅立叶变换。首先对每一行的ρi，j作镜像对称操作，得

然后进行傅立叶变换Fn，替换ρi，j(0≤n≤N)。行处理完后，对每一列进行同样的操作，得到Pm，n。

3)计算Φm，n。

4)对Φm，n作反傅立叶变换，得到解缠函数φi，j的最小二乘估算值。

实践证明，在残差点过多时，基于FFT无权重最小二乘相位解缠算法的计算结果较平滑，但与实际数据存在很大的差异，因此有必要考虑引入权重，抑制误差的传播。

将最小二乘法得到的结果进行反缠绕，发现在原缠绕条纹密集的地方，经最小二乘法解缠后反缠绕时条纹明显变稀。这是由于最小二乘法的平滑作用，使其在解缠过程中对真实相位的逼近过程中出现峰削尖、谷添底、陡坡变缓的趋势。Bamler和Adam等人［10］指出，所有线性解缠方法都不可避免非零展开误差。

3 改进加权最小二乘相位解缠

3.1 原有加权最小二乘

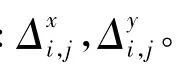
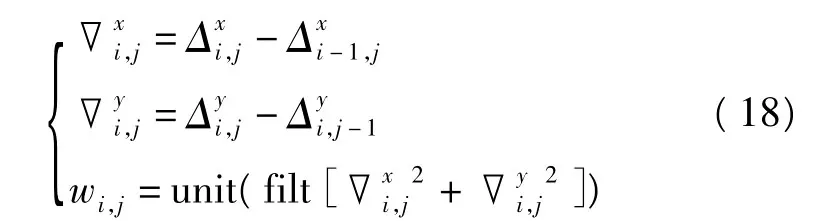
式中unit(.)为归一化处理，filt［.］为低通滤波，求出权重wi，j后，用wi，j对ρi，j进行加权处理：

式中的K为控制加权强度，其值由实验确定。权重wi，j取自二阶差分的模，它对原相位中坡度不变的区域加权为0，仅对坡度有变化的区域有实际的加权，且坡度变化越快加权越重，因此能较好的抵消最小二乘的平滑作用。计算量上较最小二乘增加的不多［7］。

在干涉图含噪声多，相位不连续，残差点过多的情况下，原有加权最小二乘法相位解缠的不足使其相比较不加权最小二乘解缠结果精度提高不多，甚至不如不加权最小二乘法，解缠效率低，耗时较长。

3.2 改进加权最小二乘法在采用加权最小二乘实现相位解缠时，权重的选取直接影响到算法的性能，甚至是决定算法成败的关键。在无法获得相干系数图的情况下，相位导数变化图是目前应用最广，同时也是较可靠的一种权重选取方法。严格来讲，相位导数变化描述了相位数据质量差的程度，而不是质量好的程度。改进的加权最小二乘相位解缠的权重依据相位导数变化图来确定，即

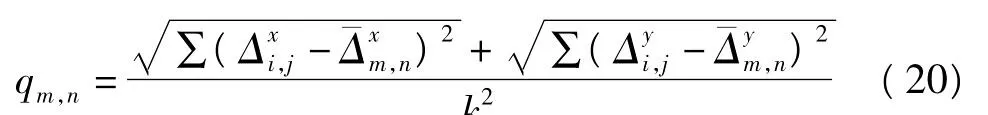
定义梯度权重为：

加权相位拉普拉斯操作数为：

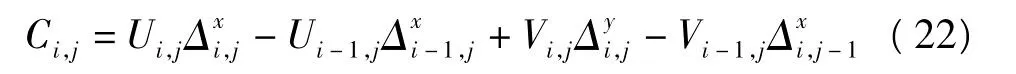
用Ci，j对ρi，j进行加权处理，即

4 实验分析

试验数据来源于济宁某地区的InSAR图像，通过GAMMA软件对其进行形变提取，裁取感兴趣区域(干涉条纹明显)，得到了去平地和滤波处理后的干涉相位图(160×146)如图1(a)所示。由于干涉相位图中仍然存在较大的噪声，经过极大似然滤波处理后干涉相位图如图1(b)所示。可以看出，滤波后干涉条纹变得明显清晰。残差点分布图如图1 (c)所示(图中黑点表示残差)，3种解缠方法的解缠结果见图23(图像右边的色度条表示相位值，单位为弧度)，解缠后重缠绕结果如图3所示。

解缠方法目视评价：

1)从残差点分布图上可以看出，残差点很多，主要分布在噪声较多的区域。

2)3种解缠方法均能成功的进行解缠，解缠结果(图2)相对比较平滑。由于各种方法对误差的控制能力不同，所以中心区域的大小不同。

3)从图3可以看出，由于最小二乘的平滑作用，重缠绕的条纹相比原缠绕条纹明显变稀。改进的加权LS解缠方法相对来说能更好的恢复干涉条纹，其他两种方法目视上区别不大。

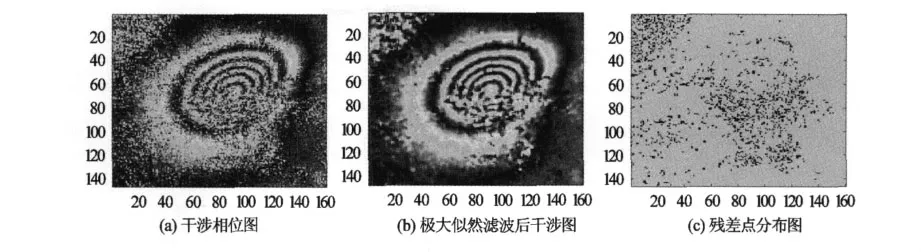
图1 去平地和滤波处理后的干涉相位Fig.1 Interfere phase after flat removing and filtering

图2 3种解缠方法的解缠结果Fig.2 Results with three unwrarpping methods

图3 解缠后重缠绕结果Fig.3 Rewrapping results after unwrapping

解缠方法定量评价：

根据不连续点数目、ε值［1］和解缠重缠绕结果与缠绕相位的差值3个指标评价改进的加权LS解缠方法的性能。不连续点数目越小，抗相位畸变的性能越好;ε值越小，则解缠质量越高;解缠重缠绕结果与缠绕相位的差值越小，可靠性越好。表1给出了3种方法的不连续点数目、ε值和解缠时间。表2给出了3种方法解缠重缠绕结果与缠绕相位的差值指标。

表1 3种解缠方法不连续点数目、ε值和解缠时间表Tab.1 Comparison among discontinuous point numbers，ε values and time of phase unwrapping with three unwrapping methods

表2 3种解缠方法解缠重缠绕结果与缠绕相位的差值表Tab.2 Differences between rewrapped results with three unwrapping methods and original wrap phase

从表1～2可以看出，改进的加权LS解缠方法不连续点数目和值、误差绝对值的均值和中误差均小于其他两种解缠方法。解缠时间较不加权LS解缠方法增加的不多。说明本文改进方法在残差点过多的情况下，抗相位畸变能力更好，解缠质量更高，可靠性更好。而原有加权最小二乘方法在本实验中对于噪声多，残差点丰富的干涉图解缠结果反而在解缠质量和效率上都不如不加权LS解缠方法，这也证明了传统加权方法的不足。

4 结论

针对基于FFT变换的不加权LS解缠方法和原加权LS解缠方法在残差点过多情况下解缠结果较平滑这一情况，提出了一种利用相位导数变化图进行加权改进的算法。利用真实数据，在目视和定量两个方面分析和评价了3种方法的性能。试验证明，改进的算法在残差点过多的情况下，具有更好的抗相位畸变能力以及更高的解缠质量和可靠性。本文提出的算法不仅对小像元图像适用，对于较大型程序的编制和干涉图的解缠也有一定的适用性和参考价值。

1 Ghiglia D C and Pritt M D.Two-dimensional phase unwrapping：Theory，algorithms and software［M］.John Wiley＆Sons，1998.

2 Ghiglia D C and Romero L A.Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods［J］.J Opt Soc Am A.，1994，11(1)：107-117.

3 Costantini M.A phase unwrapping method based on network programming［A］.Proc.Fringe’96 Workshop-ERS SAR interferometry［C］.Zurich：［s.n.］，1996.

4 刘国林，等.卡尔曼滤波在InSAR噪声消除与相位解缠中的应用［J］.大地测量与地球动力学，2006，(2)：66-70.

5 Dias J M B and Leitao J M N.InSAR phase unwrapping：a Bayesian approach［J］.Geoscience and Remote Sensing Symposium，2001，IGARSS'01：396-400.

6 赵争，张继贤，张过.遗传算法在InSAR相位解缠中的应用［J］.测绘科学，2002，27(3)：37-40.

7 许才军，王华.InSAR相位解缠算法比较及误差分析［J］.武汉大学学报(信息科学版)，2004，29(1)：67-71.

8 Mark D，Pritt and Jerome S Shipman.Least-squares two-dimensional phase unwrapping using FFT’s［J］.IEEE Trans，1994，32(3)：706-708.

9 李平湘，样杰.雷达干涉测量原理与应用［M］.北京：测绘出版社，2006.

10 Bamler R，et al.Nosie-induced slope disotrion in 2-D phase unwrapping by linear estimators with application to SAR interferometry［J］.IEEE Trans，1998，36(3)：913-921.

AN IMPROVED ALGORITHM OF WEIGHTED LEAST-SQUARES FOR PHASE UNWRAPPING

Dong Chunmin1)，Liu Guolin1，2)，Yu Shengwen1)，Liu Weike1)and Zhou Wei1)

(1)Geomatics College，Shandong University of Science and Technology，Qingdao 266510 2)Key Laboratory of Surveying and Mapping Technology on Island and Reef，State Bureau of Surveying and Mapping，Qingdao266510)

Phase unwrapping is the key step in topographic elevation mapping and reconstruction of three-dimensional terrain model by Interferometric Synthetic Aperture Radar(InSAR).Considering the problem that the existing weighted and unweighted least-squares phase unwrapping results need smoothing，an improved algorithm using phase derivative variance map based on the principle of Least-squares phase unwrapping is proposed.With the real InSAR data，by comparison of the improved algorithm with the existing weighted and unweighted least-squares algorithm，it is verified that the proposed algorithm can effectively deal with the situation that there are too many residues and can get a higher accurate and reliable phase unwrapping results.

InSAR;phase unwrapping;weighted least-squares;phase derivative variance;residue

1671-5942(2011)Supp.-0090-05

2011-01-16

国家自然科学基金(40874001);海岛(礁)测绘技术国家测绘局重点实验室资助项目(2010A01)

董春敏，女，1985年生，山东滨州人，硕士，主要从事现代测量数据处理理论及应用研究.E-mail：chunmin0919@126.com

P227

A