量子力学中算符微商浅析

李新克

(湖北汽车工业学院科技学院，湖北 十堰 442002)

量子力学中算符微商浅析

李新克

(湖北汽车工业学院科技学院，湖北 十堰 442002)

结合具体例子，介绍了量子理论中几种不同情况下算符微商的定义、运算法则和计算方法，以帮助学生掌握算符的微商运算。

量子力学；算符运算；微商

量子系统的运动状态用态矢量描述，而物理量则需要用相应的线性厄米算符作用到态矢量上获得[1]。算符的运算方法与数字的运算方法有很大不同，常常成为学习量子理论的拦路虎。而在量子力学、量子光学等学科的学习当中，经常会遇到算符微商的问题[2]，但是许多教材都没有详细讨论，致使一些学生在学习时遇到更多困难。下面，笔者分别讨论几种不同情形下的算符微商问题❶。

1 算符对时间的微商

与平均值定义比较可得：

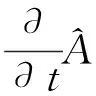
2 含参变量算符对参变量的微商

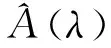
如果把算符写作矩阵形式，算符的微商即为对算符矩阵元的微商。利用这个定义可以很容易证明算符对参变量微商的一些运算法则。以经常遇到的指数形式算符为例[6]，设:

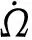
(1)

在海森堡绘景下利用式(1)可以很容易推导海森堡方程[6]：

相应的，如果把式(1)看做微分方程，其解即为:

(2)

式中，c为常数。

3 算符函数对算符的微商

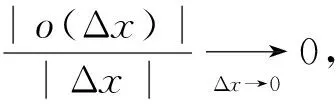
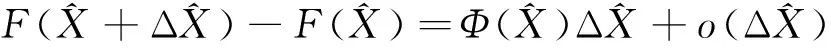
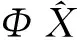
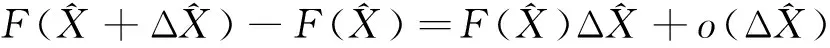
可得：

4 结 语

介绍了量子理论中算符和算符函数微商在几种常见情况下的定义和运算法则，并举例进行了说明。在了解和掌握这些内容之后，算符微商的问题就会逐渐地得心应手，能大大提高量子理论的学习效率。

[1]狄拉克.量子力学原理[M]. 陈咸亨 译.北京:科学出版社,1965.

[2]杨伯君. 量子光学基础[M]. 北京:北京邮电大学出版社,1996.

[3]朗道,栗弗席兹. 量子力学(非相对论理论)[M]. 北京:人民教育出版社,1980.

[4]费恩曼,莱顿，桑兹. 费曼物理学讲义 [M].李洪芳 等译. 上海:上海科学技术出版社,2005.

[5]戴岩伟. 浅谈量子力学中算符运算的多种求法[J].安徽师范学院学报,2005(2)：31-32.

[6]山卡(美). 量子力学原理[M]. 北京:世界图书出版社北京公司,2007.

[7]喀兴林. 高等量子力学[M]. 北京:高等教育出版社,1999.

[8]吴兆颜. 高等量子力学[M]. 长春:吉林大学出版社,2008.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.09.005

O413

A

1673-1409(2011)09-0010-03