带定子电阻辨识的新型滑模速度观测器

李国华，廉兆军，王继强

(辽宁工程技术大学，辽宁葫芦岛125105)

0 引 言

在无速度传感器的异步电动机调速系统中，获得转速信号的方法基本上有三条思路:开环计算转速、闭环构造转速和利用电动机结构上的特征提取转速信号［1］。常用的转速辨识方法主要有直接计算法、模型参考自适应法、观测器法、转子齿谐波法、扩展卡尔曼滤波法、高频注入法和智能控制法等［2－5］。无速度传感器技术的核心问题是对磁链和转速的观测［5］。在磁链观测中，电压模型不含有转子电阻和转子时间常数，因此可以有效降低转子参数变化的影响。但电压模型主要存在两方面的问题:①纯积分环节会产生直流漂移和初始值问题;②定子电阻变化对磁链观测精度的影响。尤其在低速范围内，上述问题的影响更加明显。在转速观测中，目前广泛使用的PI自适应率的参数整定比较复杂，如何选择更合理有效的替代方法也是值得研究的问题［6］。

近年来，电机滑模控制技术发展迅速，并取得一定的进步。文献［7－9］分别提出了异步电动机的滑模速度观测方法，并取得了较好的效果，但均未考虑电机定、转子电阻变化对磁链和转速观测精度的影响。本文提出了一种带定子电阻辨识的新型滑模速度观测器。采用一种改进的电压转子磁链模型，在降低转子电阻变化影响的同时，有效解决了纯积分电压模型中的直流漂移和初始值问题;并通过定子电阻的在线辨识来降低定子电阻变化的影响;与广泛使用的PI自适应率相比，滑模观测器在转速观测中需要设定的参数只有一个，从而降低了参数整定的复杂性。

1 异步电动机的状态方程

在两相静止αβ坐标系下，以定子电流和转子磁链为状态量的异步电动机状态方程如下:

2 带定子电阻辨识的新型滑模速度观测器

图1为带定子电阻辨识的新型滑模速度观测器的原理框图，主要分为定子电流计算、定子电阻辨识、改进电压转子磁链模型和滑模速度辨识四部分，该观测器输入量是定子电压和定子电流的实际值，输出量是电机转速的观测值。

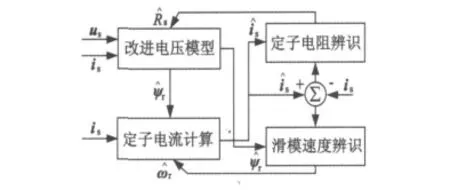
图1 新型滑模速度观测器框图

2.1 定子电流计算和定子电阻辨识

在异步电动机状态方程的基础上，选择定子电流为系统的反馈信号，并定义定子电流估计值与实际值之差作为误差信号，G为反馈矩阵，可得以定子电流为状态量的自适应伪降阶观测器:

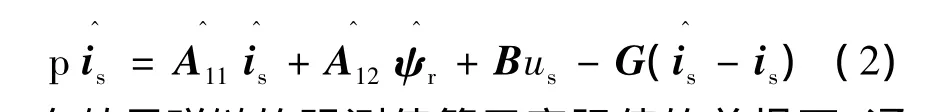
在转子磁链的观测值等于实际值的前提下，通过式(1)、式(2)可得观测器状态误差方程:

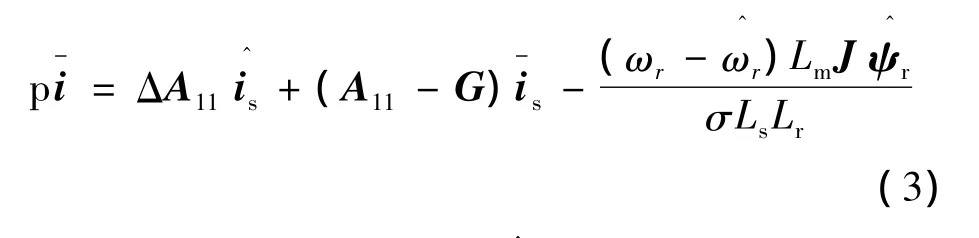
式中:ΔA11=A11是定子电阻辨识值，定子电流误差

根据李雅普诺夫稳定性理论，在转速稳定时，将定子电阻视为变化的参数，可得定子电阻PI自适应估算公式［10］:

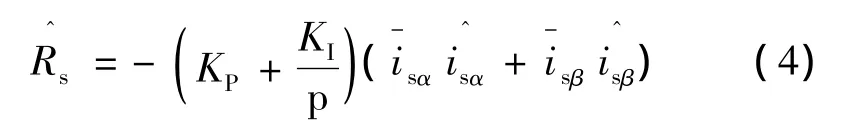
式中:KP和KI为待定常数。

在电机的实际运行中，由于绕组温度变化和集肤效应的影响，会使定子电阻发生变化，直接影响磁链和转速的观测精度。准确的定子电阻辨识为实现磁链和转速的精确观测奠定了基础。

2.2 改进电压模型

传统观测器法中转子磁链的观测多采用电流模型，易受转子参数变化的影响。由于本文的定子电阻辨识是在假设转子磁链的观测值等于实际值的前提下进行的，因此在保证磁链观测准确的情况下，采用哪种磁链模型对系统的正常工作没有影响。为降低转子参数变化对系统的影响，本文选择了电压模型进行转子磁链观测。传统电压模型中的纯积分环节会产生直流漂移和初始值问题，而初始值问题的最终影响同样是产生直流偏置误差。在电机的实际运行中，电压模型输入的反电动势中直流成分的存在是无法避免的，经过积分项的累积，最终会产生很大的直流漂移［11］。

文献［12］采用一种新颖的电压磁链模型观测定子磁链，取得了较好的观测精度。本文将该方法应用于转子磁链的观测中，并给出改进的电压转子磁链模型(简称改进电压模型)的原理图、仿真模型图和验证结果。图2a为改进电压模型的原理图，图中ωe为电机同步角频率。假设模型输入的反电动势为:

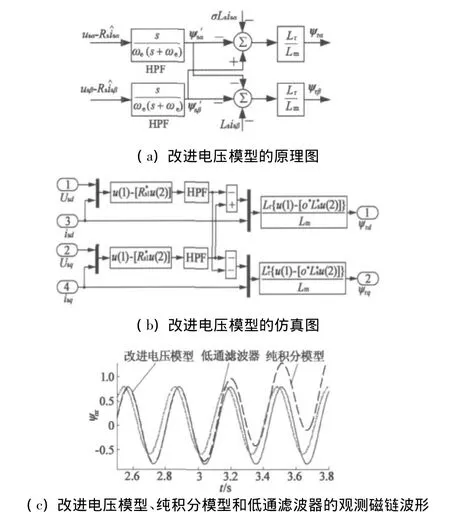
图2 转子磁链观测器及其观测磁链的波形

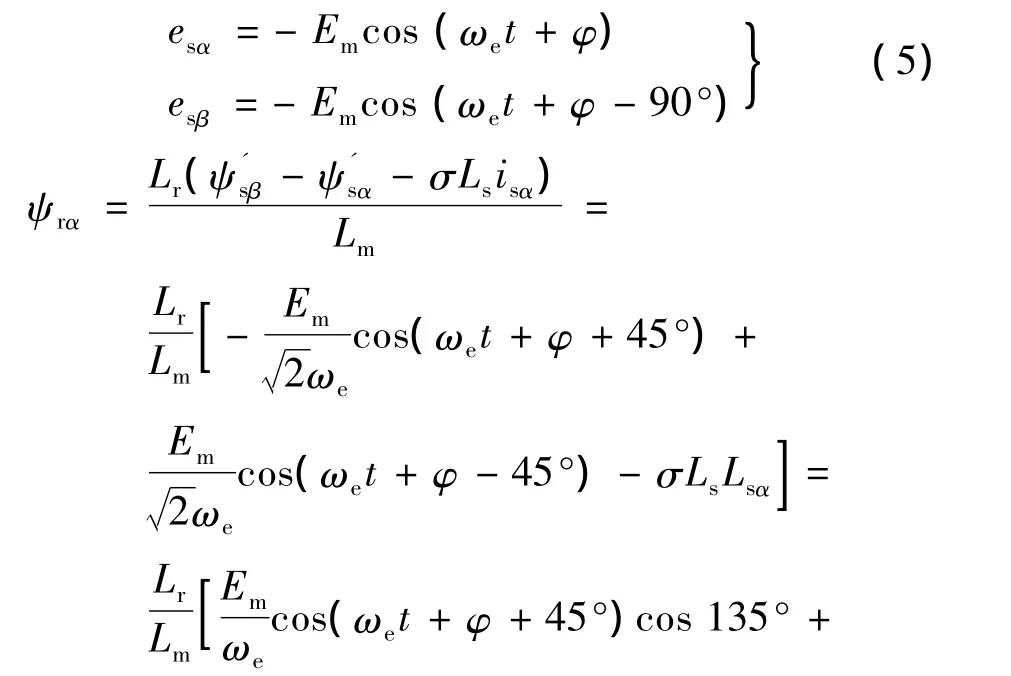
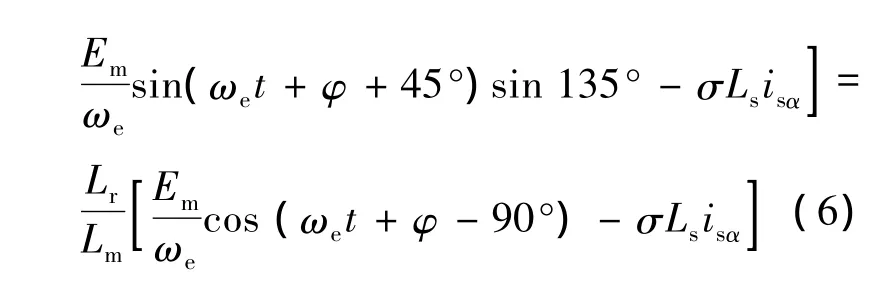
同理可得:

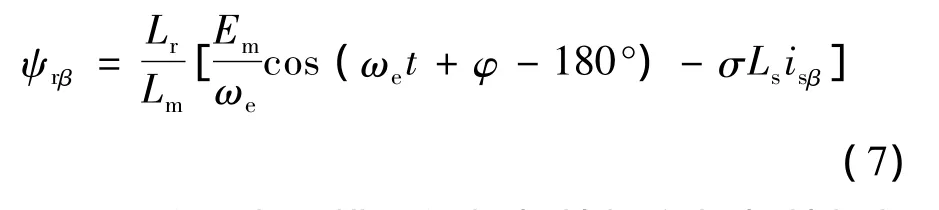
可见，改进电压模型的幅频特性和相频特性与纯积分电压模型一致，但改进电压模型的直流增益为零，而纯积分电压模型的直流增益为无穷大。因此改进电压模型可以有效抑制直流漂移和初始值问题，而且不会引入幅值和相位上的误差。图2b是改进电压模型在Matlab/Simulink环境下的仿真模型。图2c是在反电动势中突然加入1 V直流分量的情况下，改进电压模型、低通滤波器和纯积分电压模型分别观测的转子磁链波形。由波形图可见，纯积分模型的观测磁链波形中有明显的直流漂移;低通滤波器虽然抑制直流偏置引起的发散现象，但其观测磁链波形中含有明显的直流成分，而且在幅值和相位上都存在一定误差;而改进电压模型可以解决纯积分模型和低通滤波器中存在的问题，实现转子磁链的准确观测。

2.3 滑模速度辨识

滑模控制技术具有响应速度快、对系统参数变化及扰动不灵敏、无需在线辨识、工程实现简单等优点。滑模控制中的非线性和高速切换特性，非常适合异步电动机这种复杂对象的控制。

为了保证系统的全局渐进稳定性，本文根据滑模控制理论设计了滑模速度辨识方法。即:

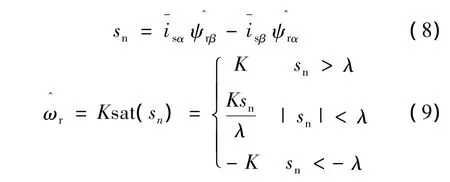
式中:K和λ为大于零的待定常数。

利用定子电流估计值与实际值之差，通过选取合适的切换函数和滑模控制律使系统的状态最终稳定在设计好的滑模超平面上，从而实现电机转速的准确观测。

文献［7－9］证明了当K足够大时，观测器所确定的滑动模态存在且可达，滑模观测器的等效速度会收敛于真实转速，且定子电流和转子磁链具有稳定性。但是K值越大，观测转速的抖动会越大，甚至出现不收敛的情况。因此，式(9)采用光滑连续的饱和函数代替常用的符号函数，以抑制观测转速中的高频抖动现象。

3 仿真结果及分析

为验证本文提出的带定子电阻辨识的新型滑模速度观测器(简称新方法)的性能，在Matlab/Simulink仿真环境下建立异步电动机无速度传感器的矢量控制系统，在仿真过程中分别改变电机的转子电阻值和定子电阻值，对该方案进行验证。并在相同条件下，与无定子电阻辨识的滑模观测器进行对比分析。

系统的参数:Rs=0.935 Ω，Rr=0.731 Ω，Ls=0.083 H，Lr=0.083 H，Lm=0.079 H;负载TL=1.8 N·m;转子磁链给定值为0.8 Wb;滑模速度辨识中的待定参数λ=0.003，K=185;定子电阻辨识中，KP=0.005，KI=50;仿真时间为0～8 s;在2 s时，将转子电阻升高至原值的1.5倍;在4 s时，将定子电阻升至原值的1.2倍。

由图3可见，在电机给定转速为10 rad/s的情况下，新方法可以准确地辨识定子电阻，并实时更新观测器中的定子电阻值，以降低在电机实际运行中定子电阻变化所带来的影响;由于新方法采用了改进电压模型观测转子磁链，因此转子电阻在2 s时的变化对转子磁链观测没有影响，转速观测波形虽然有所波动，但很快恢复至给定值;4 s时定子电阻值发生变化，在无定子电阻辨识的滑模观测器中，转子磁链和转速的观测波形都出现较大误差，明显偏离了给定值;而在新方法中，由于定子电阻的准确辨识，观测磁链和观测转速没有受到定子电阻变化的影响。

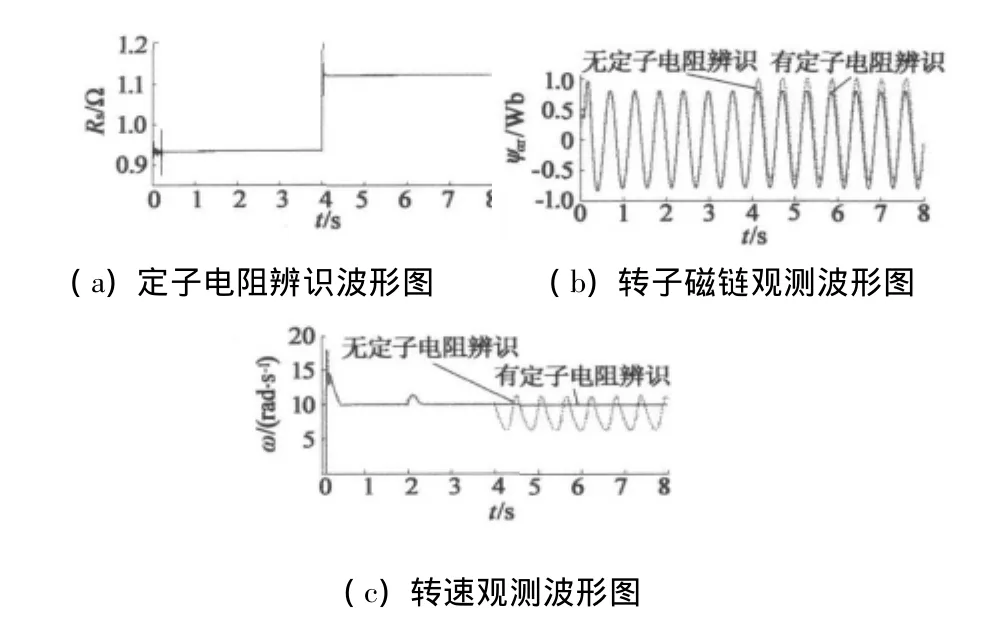
图3 给定速度为10 rad/s时的波形图

由图4可见，在电机给定转速为100 rad/s时，新方法同样可以较准确地辨识定子电阻。在整个仿真过程中，观测磁链和观测转速的波形稳定，能够准确地跟踪给定值，响应速度快，而且观测转速波形中不存在高频抖动问题;而在无定子电阻辨识的滑模观测器中，观测磁链和观测转速都受到了定子电阻变化的影响，出现一定程度的误差，但与低速范围内的工作情况相比，误差相对较小。

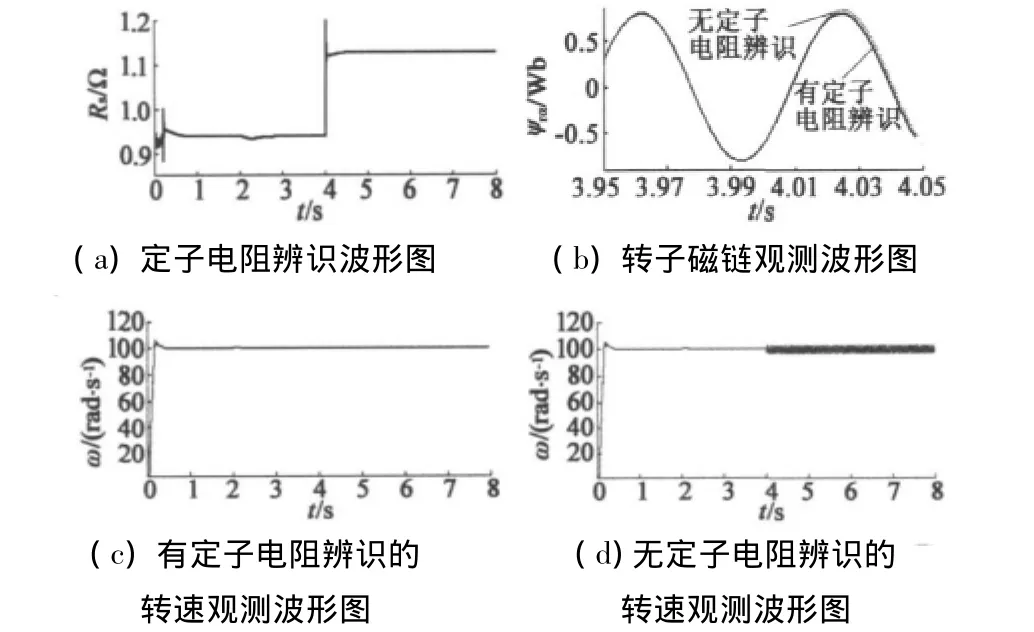
图4 给定转速为100 rad/s的波形图

4 结 语

本文利用滑模变结构控制理论提出了一种带定子电阻辨识的新型滑模速度观测器。在准确辨识定子电阻和转子磁链的基础上，实现了异步电动机电机转速的精确观测。与传统方法相比，该观测器在全速范围内具能够更加准确地观测电机的转速和转子磁链，对定、转子电阻变化具有较强的鲁棒性。

［1］ 陈伯时，杨耕.无速度传感器高性能交流调速控制的三条思路及其发展建议［J］.电气传动，2006，36(1):3－8.

［2］ OHYAMA K，ASHER G M，SUMNER M.Comparative analysis of experimental performance and stability of sensorless induction motor drives［J］.IEEE Trans.Industrial Electronics，2006，53(1):178－186.

［3］ GAO Q，ASHER G，SUMNER M.Sensorless position and speed control of induction motors using high－frequency injection and without offline pre－commissioning［J］.IEEE Trans.Industrial Electronics，2007，54(5):2474－2481.

［4］ 赵争鸣，袁立强.电力电子与电机系统集成分析基础［M］.北京:机械工业出版社，2009:176－181.

［5］ 王文森，李永东，王光辉，等.基于PI自适应法的无速度传感器异步电动机矢量控制系统［J］.电工技术学报，2002，17(1):1－6.

［6］ 李华德，李擎，白晶.电机拖动自动控制系统［M］.北京:机械工业出版社，2009:226－229.

［7］ 张细政，王耀南，杨民生.新型感应电机自适应观测与滑模控制策略［J］.煤炭学报，2009，34(8):1144－1138.

［8］ 王庆龙，张崇巍，张兴.交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识［J］.中国电机工程学报，2007，27(15):70－74.

［9］ 路强，沈传文，季晓隆，等.一种用于感应电机控制的新型滑模速度观测器研究［J］.中国电机工程学报，2006，26(18):164－168.

［10］ 王成元，夏加宽，孙宜标.现代电机控制技术［M］.北京:机械工业出版社，2008:186－192.

［11］ 李永东，李明才.感应电机高性能无速度传感器控制系统－回顾、现状与展望［J］.电气传动，2004，34(1):4－10.

［12］ 王宇，邓智泉.一种新颖的电机磁链辨识算法［J］.中国电机工程学报，2007，27(6):39－43.