筒仓中粮食卸料动压力的数值模型
程绪铎 唐福元 石翠霞 陆琳琳
(南京财经大学食品科学与工程学院,南京 210003)
筒仓中粮食卸料动压力的数值模型
程绪铎 唐福元 石翠霞 陆琳琳
(南京财经大学食品科学与工程学院,南京 210003)
筒仓中粮食卸料时拱不断形成并不断坍塌。以这些不稳定拱(瞬态拱)为依据,建立一个预测筒仓中粮食卸料动压力的数值模型。将粮食分成许多薄层,结拱层上方的粮食视为多层弹簧振子系统,建立该系统的振动方程,从而解出结拱层的加速度,再对结拱层运用动量定理,推导出粮食卸料时对仓壁的动压力。计算结果表明:粮食卸料时粮食对筒仓壁产生的动压力大于Janssen方程计算的储藏静压力,粮食卸料时超压因子随粮食深度的增加而增加,对于直径 10 m 的筒仓(ρ=800 kg/m3,φ =25.0°,μ =0.4,Q=1.0 kt/h,ν =0.4,Ev=30.0 MPa),粮食深度从2.0 m 增加到 24.0 m 时,超压因子从约 1.33 增加到 1.87;粮食卸料时超压因子随粮食流量的增大而增大,随粮食体积弹性模量的增大而增大,随粮食和仓壁摩擦系数的增大而增大,随粮食内摩擦角的增大而减小;储藏静压力和卸料动压力都随粮食和仓壁摩擦系数的增大而减小,都随粮食内摩擦角的增大而减小。
筒仓 粮食卸料 结拱 超压因子
筒仓中粮食卸料动压力的研究从20世纪中叶开始,一直持续到现在[1-5]。筒仓中粮食卸料时粮食对仓壁产生的动压力的研究是从理论和试验两个方向进行的。Moriyama等[6]提出的粮食动压力是粮食卸载时仓内粮食由主动应力状态转换成被动应力状态的结果。这个理论很难确定主动应力状态转换成被动应力状态的条件和区域。Xu S等[7]提出粮食动压力是粮食卸料时仓内粮食横向膨胀的结果,当粮食卸料时,由于粮食的相对运动,竖直方向的剪切产生,剪切可视为两个带锯齿表面的刚块的竖直剪切,这样,粮食水平方向膨胀发生,这个膨胀决定于锯齿表面的膨胀角,但这个理论的问题是膨胀角很难确定。苏乐逍等[8]提出筒仓卸料时,粮食不断地结拱,又不断地塌拱,由于结拱就阻碍了拱以上部分粮食的流动,而使其速度很快减为零.同时产生一与流速方向相同的惯性力,此惯性力与拱上部粮食质量全部由拱来承担,从而使仓壁在拱脚处受到了比粮食储藏时大得多的压力。但这个惯性力很难确定。许多研究者用试验测量模型仓和实际仓的仓墙压力[9-13]。Takhtamishev 在圆筒仓试验中测出卸仓超压因子在2到3之间;Platonov和Kovtun在高与直径的比为6.67的圆筒仓试验中测出超压因子在 1.67 到 2.32 之间[12]。Manbeeck 等[13]对平底深仓(H/D=5)进行卸仓试验,得出超压因子是0.7到2.4。研究发现许多因数对最大动压力有影响,这些因数是粮食颗粒大小、卸料速率、仓高与直径的比、仓墙沟纹、漏斗设计、卸料偏心率、仓墙刚度。研究结果一致表明卸料时作用于仓墙上动压力超过由Janssen方程预计的静压力。然而,对于动态压力的大小和位置,试验结果是不一致的,动压力与静压力之比从较低的1.25~1.5到较高的 3.5 ~4.0[12]。
基于结拱(瞬态拱)理论,将结拱时拱上方的粮食分成等厚的许多层,将其简化成多层弹簧振子系统,从而求出结拱时粮食流动时的惯性力,进而有动量定理求出粮食对仓壁的动压力。
1 粮食储藏时对仓壁的侧压力
粮食静止储藏时,粮食处在主动应力状态。假设粮食密度ρ、仓墙和粮食间摩擦系数μ、内摩擦角φ是常数,压力大小不随半径的大小和方向而变化。图1是一个圆筒仓和粮食表面下深度y处粮食微元层示意图。

图1 筒仓内微元层受力图
作用于微元层上竖直方向的合力等于0:

式中:A为仓的横截面面积,C为仓的周长,dy为是粮食层厚度,g为重力加速度,phs为粮食内侧压应力,pvs为粮食内竖直压应力。
粮食处在主动应力状态时侧压应力和竖直压应力之比ks为:

将式(2)代入式(1),得粮食内竖直压应力表达式为:

式中:R=A/C为仓内水力半径。
作用在仓墙上的侧压力为:

2 粮食卸料结拱时的动压力
2.1 粮食卸料结拱时的动压力公式
设t时刻在深度y处结拱,由于结拱,使正在以速度v流动的粮食突然减缓下来,流速迅速达到零,故产生一惯性力,其方向与粮食的流速方向相同。
粮食结拱层受力图见图2。

图2 粮食结拱层受力图
取结拱处的粮食薄层dy,将粮食薄层的动量及上下粮食压力对其冲量在y轴上投影,应用动量定理,则有

式(5)、式(6)简化得:

式(8)代入式(7)得:

积分式(9),并代入初始条件pv(0)=0,得谷物卸料结拱时的竖直压应力与侧向压应力为:

比较式(4)、式(11)得超压因子为:

2.2 粮食卸料结拱时的惯性加速度的确定
由式(11)、式(12)知,要求得粮食卸料结拱时的侧向压应力和超压因子的值需先确定粮食薄层的惯性加速度的值。
2.2.1 筒仓中粮食系统的弹簧振子模型
将筒仓中拱上方的粮食分为n层,每层的厚度相等为d,质量相等为m,且有,

式中:D为筒仓圆筒部分的直径,Hg为筒仓圆筒中拱上部的高。
假设每相邻两层被一个弹簧连接。第i层的压缩值 λi为:

式中:k为筒仓中粮食每层的刚度。
筒仓中拱的上方粮食系统被简化成多层弹簧振子系统(图3、图4)。

图3 筒仓内粮食系统

图4 筒仓内粮食系统的振动模型
选各粮食层的高度z1,z2,…,zn为系统的广义坐标,振动时,系统的动能为:

式中:m为各层的质量。
系统的弹性势能为:

系统的重力势能为:

系统的总势能为:

系统的广义力为:

式中:M为拱的上方谷物的总质量,且M=nm。
系统的Lagrang方程为:

将式(16)~式(21)代入 式(22),得系统的动力学方程为:

其中,z·
i为第 i层的速度,z¨i为第 i层的加速度。
系统各层的初位置为:

系统各层的初速度为:

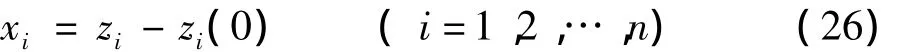
系统各层的位移为:结合式(23),式(24),式(26),系统的动力学方程变为:

其中,x·i为第i层的速度,x¨i为第i层的加速度。令:结合式(27),式(28),得系统的动力学方程组为:


系统的初始条件为:

求解微分方程组 (29),可得各层的位移xi,速度x·i,加速度x¨i.结拱层的粮食惯性加速度为:

2.2.2 筒仓内粮食各层刚度的确定粮食的各层刚度有下式确定:

式中:E为粮食弹性模量,EV为粮食的体积弹性模量。
2.2.3 筒仓中圆筒部分粮食流速的确定

圆筒部分粮食流速有下式确定:式中:Q为粮食体积流量,Qz为粮食质量流量。
3 数值结果和分析
在模型的计算中,选择的参数为:筒仓直径D=10 m,筒仓圆筒高H=24 m,粮食密度ρ=800 kg/m3,粮食内摩擦角 φ =20°,25°,30°,粮食和仓壁摩擦系数 μ =0.2,0.3,0.4,粮食体积弹性模量 EV=10,30,50 MPa,粮食泊松比 ν=0.4,卸载流量 Q=0.6,1.0,1.4 kt/h,各层粮食的厚度 ΔH=0.2 m。数值结果如图5~图12所示。
图5、图7、图9、图11表示粮食卸料时的超压因子,超压因子随粮食深度的增加而增加,对于直径10 m的筒仓,粮食深度从2.0 m增加到24.0 m时,超压因子从约1.33增加到1.87。这个结果是在已报告的试验结论(从低的超压因子1.25~1.5到高的3.5 ~4.0)[12-13]范围内的。图6、图8、图10、图12表示粮食储藏时和粮食卸料时粮食对仓壁的侧压力,卸料动压力比储藏静压力大。图5表示超压因子随卸料流量的增大而增大。图6表示卸料动压力随流量的增大而增大。图7表示超压因子随粮食体积弹性模量的增大而增大。图8表示卸料动压力随粮食体积弹性模量的增大而增大。图9表示超压因子随粮食和仓壁摩擦系数的增大而增大。图10表示储藏静压力和卸料动压力都随粮食和仓壁摩擦系数的增大而减小。图11表示超压因子随粮食内摩擦角的增大而减小。图12表示储藏静压力和卸料动压力都随粮食内摩擦角的增大而减小。



4 结论
4.1 谷物卸料时谷物对筒仓壁产生的动压力大于储藏静压力,谷物卸料时超压因子随谷物深度的增加而增加,对于直径10 m的筒仓,粮食深度从2.0 m增加到24.0 m 时,超压因子从约1.33增加到1.87。4.2 谷物卸料时超压因子随谷物流量的增大而增大、谷物卸料时超压因子随谷物体积弹性模量的增大而增大、谷物卸料时超压因子随谷物和仓壁摩擦系数的增大而增大、谷物卸料时超压因子随谷物内摩擦角的增大而减小。
4.3 储藏静压力和卸料动压力都随谷物和仓壁摩擦系数的增大而减小、储藏静压力和卸料动压力都随谷物内摩擦角的增大而减小。
[1]Dale A C,Robinson R N.Pressure in deep grain storage structures[J].Agricultural Engineering,1954,35(8):570 -573
[2]Deutsch G P,Sechmidt L C.The pressure on silo walls[J].Trans.ASAE.1969,91(1):450 -459
[3]赖姆伯特别M L,赖姆伯特别A M.筒仓理论与实践[M].顾华孝,译.北京:中国建设出版社,1981
[4]Jamieson J A.Grain pressures in deep bins[J].Engineering News,1904,51(10):236 -243
[5]Zhang Q,Britton M G.A micromechanics model for predicting dynamic loads during discharge in bulk solids storage structures[J].Canadian Biosystems Engineering[J],2003,45:521-527
[6]Moriyama R,Jotaki T.An inverstigation of wall pressures in flowing and static bulk materials in model bins[C].//Proceedings of Conference on Design of Silos for Strength and Flow.England:University of Lancaster,1980:22
[7]Xu S,Zhang Q,Britton M G.Effect of grain dilatancy on dynamic loads in grain bins[C].//ASAE Paper No.93 -4504.St.Joseph,MI;ASAE.1993:15
[8]苏乐逍,赵霖,刘建秀.粮食立筒仓弹性变形对卸料动压力的影响与计算[J].工程力学,1999,16(6):102-106
[9]Caughey R A,Tool C W.Lateral and vertical pressure of granular material in deep bins[J].Lowa Eng.Exp.Station Bull.172.Ames,IA,1951:32
[10]Turitzin A M.Dynamic pressure of granular material in deep bins[J].Struc.div.Am.Soc.Civil Eng.1963,89(2):49 -73
[11]Usry J L,Thompson S A.Loads on vertical stiffeners on corrugated grain bins[J].Trans.ASAE.1986,29(5):1355 -1363
[12]Digvir S,Noel D G.Stored Grain Ecosystems[M].New York:Marcel Dekker,1995:465
[13]Manbeck H B Dynamic over-pppressure in model bins during emptying[C].//Paper No.77 - 4505.Am.Soc.Agric.Eng.,St.Joseph,MI.1977:25.
Numerical Model of Dynamic Pressure of Grain Acting on Silo during Discharge
Cheng Xuduo Tan Fuyuan Shi Cuxia Liu Linlin
(College of Food Science and Engineering,Nanjing University of Finance and Economics,Nanjing 210003)
For reasonably determining the parameters of saccharification technology for extruded rice as beer adjunct,the influential regularity of the parameters of saccharification technology for extruded rice as beer adjunct on iodine value observed was studied through laboratory experiments.These parameters included saccharification time of 65℃,saccharification time of 71℃ and addition level of thermostable α - amylase.The research results indicated the extruded rice might be used as beer adjunct.Meanwhile,the iodine value of mash for extruded rice was 0.13,48%less than the traditional non - extruded rice.In addition,it was proved with chemical analysis of mash that the extruded rice could be used as beer adjunct.
extrusion,beer adjunct,saccharification,iodine value
TS210.4
A
1003-0174(2011)04-0089-06
国家科技支撑计划(2009BADA0B04-5)
2010-04-08
程绪铎,男,1957年出生,教授,粮食储藏
