数学分析教材研究 (二)*
郎开禄
(楚雄师范学院数学系,云南 楚雄 675000)
数学分析教材研究 (二)*
郎开禄
(楚雄师范学院数学系,云南 楚雄 675000)
本文阐述了数学分析课程,数学分析课程教学内容,数学分析课程教学目标,数学分析课程教学方手段,数学分析课程教学理念,数学分析教与学的基本关系;研究了两套历史悠久的数学分析沃土教材的独特风采、独异风格。
数学分析;教材;研究
3.3.3 风采三:函数级数和函数分析性质
(1)《数学分析讲义》(下册)函数级数和函数分析性质的处理思路和方法《数学分析讲义》(下册)直接证明定理8、定理9、定理10.
(a)每个un(x)在区间I连续;
(a)每个un(x)在区间I连续;
(a)每个u'n(x)在区间I连续;
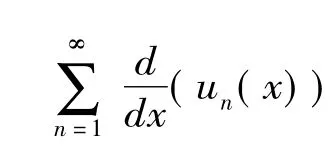
【思路和方法比较】
【ⅰ】思路和方法比较自然;
【ⅱ】思路和方法同学易理解和掌握;
【ⅲ】知识点连贯性强;
【ⅳ】思路和方法技巧性大。
(2)《数学分析》(下册)函数级数和函数分析性质的处理思路和方法
(ⅰ)直接证明定理11
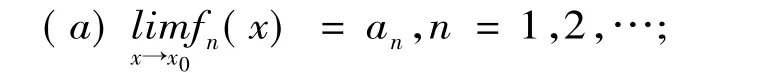
(ⅱ)应用定理11证明定理12、定理13、定理14
(a)每个fn(x)在区间I连续;
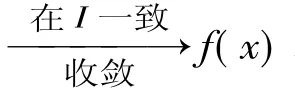
(a)每个fn(x)在区间I连续;
(a)每个f'n(x)在区间I连续;
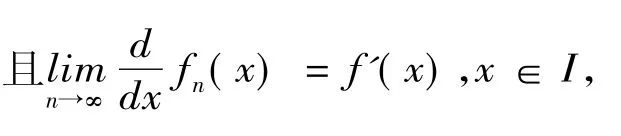
(ⅲ)应用定理12、定理13、定理14证明证明定理8、定理9、定理10证明略。
【思路和方法比较】
【ⅰ】思路和方法的关键是直接证明定理11;
【ⅱ】思路和方法陡,知识的调用要求非常高;
【ⅲ】思路和方法同学不易理解和掌握;
【ⅳ】思路和方法独特;
【ⅴ】思路和方法技巧性大。
3.3.4 风采四:含参变量无穷积分分析性质
(1)《数学分析讲义》(下册)含参变量无穷积分分析性质的处理思路和方法《数学分析讲义》(下册)直接证明定理15、定理16、定理17。
【思路和方法比较】
【ⅰ】思路和方法比较自然;
【ⅱ】思路和方法同学易理解和掌握。【ⅲ】知识点连贯性强。
【ⅳ】思路和方法技巧性大。
(2)《数学分析》(下册)含参变量无穷积分分析性质的处理思路和方法
(ⅰ)直接证明定理18
(ⅱ)应用定理18和函数级数和函数分析性质证明定理15、定理16、定理17证明略。
【思路和方法比较】
【ⅰ】思路和方法的关键是直接证明定理18;
【ⅱ】思路和方法陡,知识的调用要求非常高;
【ⅲ】思路和方法同学不易理解和掌握;
【ⅳ】思路和方法独特;
【ⅴ】思路和方法技巧性大。
3.3.5 风采五:二重积分的变量代换
(1)《数学分析讲义》(下册)二重积分的变量代换的处理思路和方法(ⅰ)直接证明定理19
定理19 若变量代换
x=x(u,v),y=y(u,v),(u,v) ∈ G'
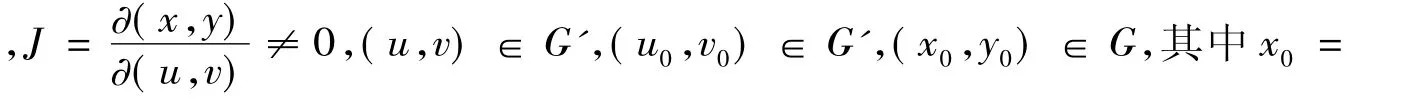
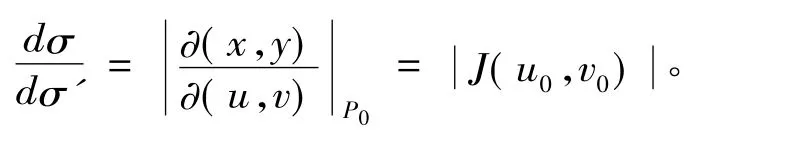
(ⅱ)应用定理19证明定理20
定理20 若变量代换
x=x(u,v),y=y(u,v),(u,v) ∈ D'
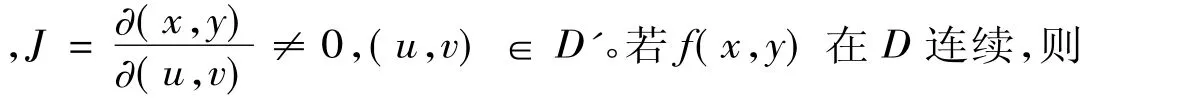
【思路和方法比较】
【ⅰ】思路和方法比较自然;
【ⅱ】思路和方法同学易理解和掌握;
【ⅲ】知识点连贯性强;
【ⅳ】思路和方法技巧性大。
(2)《数学分析》(下册)二重积分的变量代换的处理思路和方法
(ⅰ)直接证明定理21
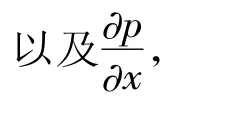
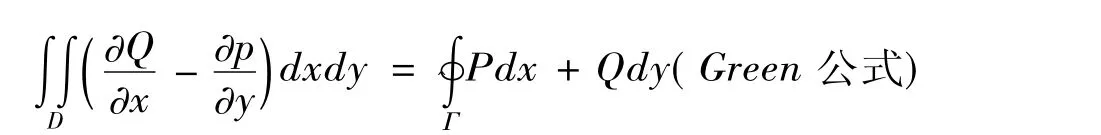
其中Γ取正向。
(ⅱ)应用定理21直接证明定理22
定理22 若变量代换
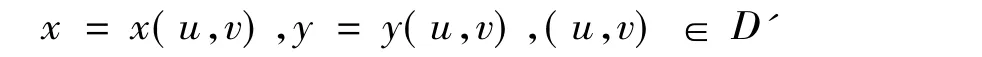
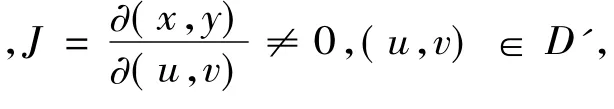
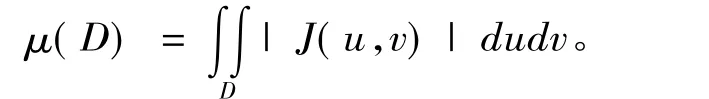
(ⅲ)应用定理22直接证明定理20
证明略
【思路和方法比较】
【ⅰ】将线积分放在重积分之前讲;
【ⅱ】思路和方法非常较陡,知识的调用要求非常高;
【ⅲ】思路和方法同学不易理解和掌握;
【ⅳ】思路和方法技巧性大;
【ⅴ】思路和方法独特。
3.3.6 风采六:定积分的可积准则
(1)《数学分析讲义》(上册)定积分的可积准则的处理思路和方法
(ⅰ)直接证明大和与小和性质
定理22 对[a,b]的任一分法T,均有
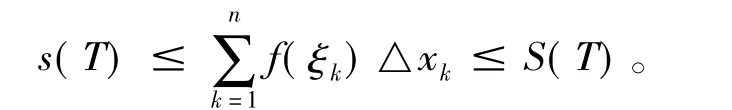
定理 23 对[a,b]任一分法 T={△1,△2,…,△n},有
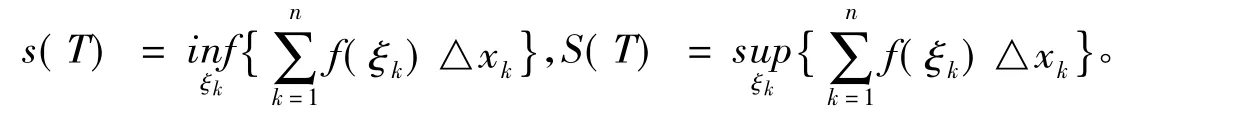
定理24 设T'是分法T添加分点得到的分法,则
S(T)≥S(T')(大和不增),s(T)≤s(T')(小和不减)。
定理25 对于[a,b]的任意分法T,T',小和不超过大和,即
s(T)≤S(T'),s(T')≤S(T)。
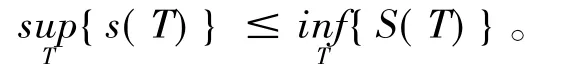
(ⅱ)应用大和与小和性质证明了可积准则
(ⅲ)应用可积准则获得了三种可积函数类
定理28(连续函数可积性)若f(x)在[a,b]连续,则f(x)在[a,b]可积。
定理29(单调函数可积性)若f(x)在[a,b]单调,则f(x)在[a,b]可积。
定理30(有有限个间断点的有界函数的可积性)若f(x)在[a,b]有界,且只有有限个间断点,则 f(x) 在[a,b]可积。
【思路和方法比较】
【ⅰ】思路和方法比较自然;
【ⅱ】思路和方法同学易理解和掌握;
【ⅲ】知识点连贯性强;
【ⅳ】思路和方法技巧性大。
(2)《数学分析》(上册)定积分的可积准则的处理思路和方法
(ⅰ)§9.3((可积条件)直接给出可积准则
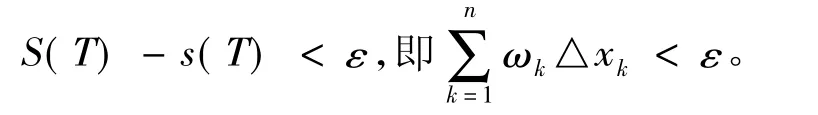
(ⅱ)§9.3可积条件应用可积准则获得了三种可积函数类。
(ⅲ)§9.8可积理论补叙证明大和与小和性质(内容较系统)。
(ⅳ)§9.8可积理论补叙应用大和与小和性质证明了可积准则(内容较系统)。
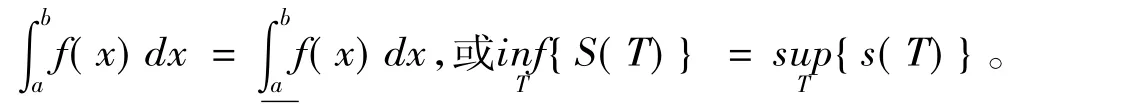
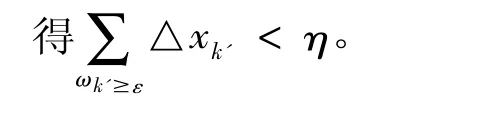
【思路和方法比较】
【ⅰ】思路和方法同学易理解和掌握;
【ⅱ】思路和方法技巧性大;
【ⅲ】思路和方法独特;
【ⅳ】知识点连贯性不强;
【ⅴ】理论性更强;
【ⅵ】获取的知识量大。
3.4 风格独异的数学分析教材
(1)《数学分析讲义》(上、下册)这套教材循序渐进,系统性强,范例和习题丰富,便于自学,且刘玉琏、傅沛仁两位先生编著了配套的《数学分析讲义学习指导书》(上、下册)(高等教育出版社出版)等教学辅导书,这样大大降低大学一年级学习数学分析的难度,也降低了备课的难度。
(2)《数学分析》(上、下册)这套教材理论性和实用性强,内容精,弹性空间大,习题丰富,富于启发,吴良森,毛羽辉,韩士安,吴畏编著了配套的《数学分析学习指导书》(上、下册)(高等教育出版社)等教学辅导书,这样大大降低大学一年级学习数学分析的难度,也降低了备课的难度。
(3)《数学分析讲义》(上、下册)和《数学分析》(上、下册)是风采独特、风格独异、历史悠久的数学分析沃土教材中的重要两部,潜心学习和研读,必然沃土发新枝。
[1]胡适耕,张显文编著.数学分析原理与方法 [M].北京:科学出版社,2008.
[2]刘玉琏,傅沛仁等编.数学分析讲义 (上)[M].第四版.北京:高等教育出版社,2002.
[3]刘玉琏,傅沛仁等编.数学分析讲义 (下)[M].第四版.北京:高等教育出版社,2002.
[4]刘玉琏,扬奎元,吕风编.数学分析讲义学习辅导书 (上)[M].第二版,北京:高等教育出版社.2003.
[5]刘玉琏,扬奎元,吕风编.数学分析讲义学习辅导书 (下)[M].第二版,北京:高等教育出版社.2003.
[6]华东师范大学数学系编.数学分析 (上) [M].第四版.北京:高等教育出版社,2009.
[7]华东师范大学数学系编.数学分析 (下) [M].第四版.北京:高等教育出版社,2009.
[8]吴良森,毛羽辉,韩士安,吴畏编著.数学分析学习指导书 (上)[M].北京:高等教育出版社.2004.
[9]吴良森,毛羽辉,韩士安,吴畏编著.数学分析学习指导书 (下)[M].北京:高等教育出版社.2004.
Research of mathematical analysis teaching materials(Part Ⅱ)
LANG Kai-lu
(Department of mathematics,Chuxiong Normal Uinversity,Chuxiong 675000,China)
This paper elucidates mathematical analysis course and its teaching content,teaching objectives,teaching method,teaching philosophy,and the relationship between teaching and learning,and then studies the unique characteristics of two profound historical versions.
Mathematical analysis;teaching materials;research
O171.2
A
1671-7406(2011)09-0024-07
2011-03-12
郎开禄 (1962—),男,云南楚雄人,副教授,主要研究方向:高等数学及数学分析。
(责任编辑 刘洪基)

