辊式矫直机矫直扭矩计算方法研究

王树环 王效岗 谢仕鸿 杨晓君

(太原科技大学，山西 030024)

矫直机是通过一组上下交错排列的矫直辊对板带材施加不同弯矩，使其发生多次弹塑性变形，从而达到消除或均匀材料残余应力的目的。矫直过程的精确分析以及精确的矫直机力能参数是合理设计和使用矫直机的重要依据。辊式矫直机在生产高强度、大规格钢板时，矫直机主传动系统及传动轴经常出现断裂事故。传动扭矩是矫直机传动系统设计的主要依据。扭矩的计算受诸多条件的影响［1］，如集中驱动的矫直机要考虑负转矩的影响，如果矫直辊集中传动，转速相同，则在矫直板材的过程中产生负转矩。负转矩现象将造成板材在矫直辊面上打滑［2］，引起噪音，从而降低了板材的矫直质量，所以不能忽略了轧件对相关各辊传动扭矩的耦合关系。辊式矫直机矫直扭矩的一般计算方法主要是根据矫直弯矩与矫直过程中矫直曲率之间的关系积分得到的，但由于对弯矩-曲率曲线的积分不易计算，故本文采用一些假设条件简化了矫直扭矩的计算。通过在某钢厂十一辊辊式矫直机上测得的矫直辊上的矫直扭矩以及电机功率的数据，验证了基于一些假设条件下的矫直扭矩的计算方法的可行性，对实际生产具有指导意义。

1 矫直扭矩的计算原理

在辊式矫直机上［3］，轧件是随着矫直辊的转动不断前进反复弯曲的。因此，矫直辊上的扭矩Mb可以按照功能相等的原理来确定，即轧件弯曲变形所做的功Ap应该和矫直辊在矫直扭矩Mb的作用下使轧件前进所做的功Ak相等。

如图1 所示，矫直过程是一个连续弯曲的过程，每个矫直单元都可视为一个矫直单元。现假设在第i 辊下，单位长度轧件的弯曲变形总曲率为，则其弯曲变形功ai，在已知轧件力矩方程M的条件下，可由下式求得：

图1 弯曲力矩延长度变化图Figure 1 Changing diagram of bending moment elongation

在图2(a)中，曲线包络的总面积是弹塑性弯曲变形功。其中，Ⅰ区是弹性变形功，Ⅲ区是弹复功。根据纯弯曲假设，可以认为，轧件通过第i 辊受到弯曲时，沿轧件长度各断面上弯曲力矩Mi值的大小只与曲率有关，而与轧件的长度无关。因此，长度为li的轧件在第i 辊上弯曲变形所做的功Api应是

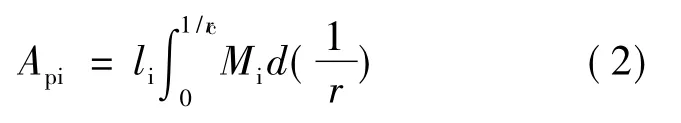
直径为D 的第i 个矫正辊，在扭矩Mbi的作用下，使轧件进行li长度所作的功Aki应是

由于Api与Aki相等，因此，

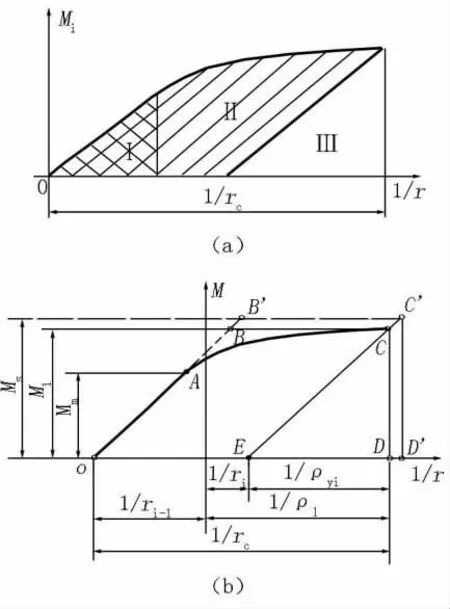
图2 轧件弹塑性弯曲变形功计算示意图Figure 2 Schematic drawing of rolled piece elastic-plastic buckling distortion work calculation

式中 D——矫直辊直径;

Mi——第i 辊处轧件断面的弯曲力;

ky——轧件弹复功恢复系数，ky=0～1，主要是针对弹复功是否耗能的问题而设。一般认为［4］，弹复时能量的释放必将反馈给矫直机。该能量虽然不易全部变成有用的能量，但绝大部分将帮助机器运行。

矫直总扭矩

2 基于假设条件的扭矩简化计算方法

为了简化矫直扭矩的计算，做如下假设：

(1)认为各辊下的弯曲力矩Mi均是塑性弯曲力矩Ms;

(2)认为弹复变形不属于耗能变形，则弹复功系数ky=0;

(3)为了简化计算，除原始曲率1/r0外，其余各辊下的残余曲率(也就是下一辊的原始曲率)都等于小变形方案中的残余曲率最大值(1/ri)max;

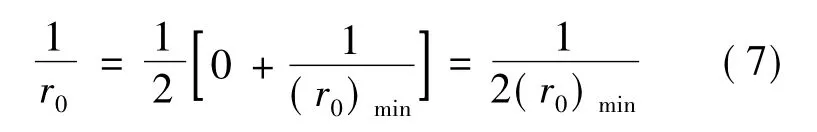
对于钢板(r0)min=(10～30)/h，h 是轧件的厚度。

按照上述假设，当矫直工件上原始曲率凸度向下部分时，矫直总扭矩应该是

矫直工件上原始曲率凸度向上部分时，矫直总扭矩应该是

式中的2 倍曲率是由于公式的假设条件，前一辊的残余曲率与本辊的原始曲率相等，而塑性变形时变形曲率是二者之和。

由于轧件上原始曲率的方向难于预先确定，因而，设总的矫直扭矩MK是的平均值。总的矫直扭矩计算式是

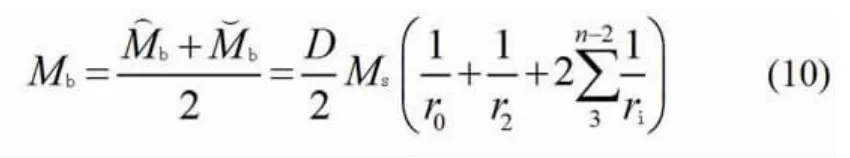
上式改写为

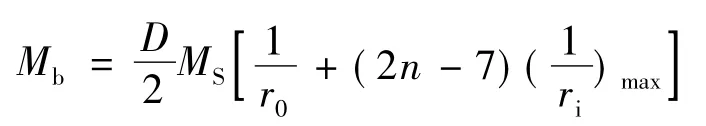
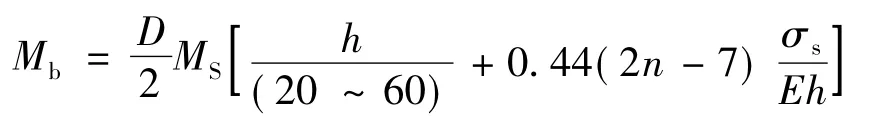
又因为MS=σsS=σsbh2/4，所以

3 矫直总扭矩及功率的计算方法

矫直辊在矫直力作用下所需克服的阻力包括轴承摩擦阻力、辊面与工件之间的滚动摩擦阻力及工件塑性变形阻力。矫直辊的总扭矩M 为［5］

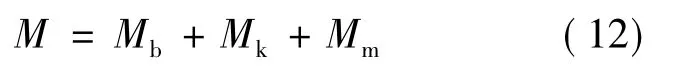
式中 Mb——轧件弯曲变形所需的力矩;

Mk——克服轧件与辊子间滚动摩擦所需力矩;

Mm——克服辊子轴承的摩擦及支承辊与工作辊间的滚动摩擦所需力矩。

3.1 轧件弯曲变形所需力矩的计算

式中 b——矩形工件的宽度;

D——矫直辊直径;

h——矩形工件的厚度;

n——矫直机辊数，此处为11;

σs——屈服强度;

E——弹性模量。

3.2 Mk的计算

式中 Fi——各辊的矫直力;

f——轧件与辊子间滚动摩擦系数，对于热矫钢板，取值为f=0.2 mm。

3.3 Mm的计算

式中 μ1——工作辊和支承辊轴承摩擦系数，滚动轴承μ=μ1=0.005;

d1——工作辊和支撑辊轴承处直径，滚动轴承取中径;

f1——工作辊与支撑辊的滚动摩擦系数，一般取为0.05 mm;

φ——工作辊与支承辊的交错角。

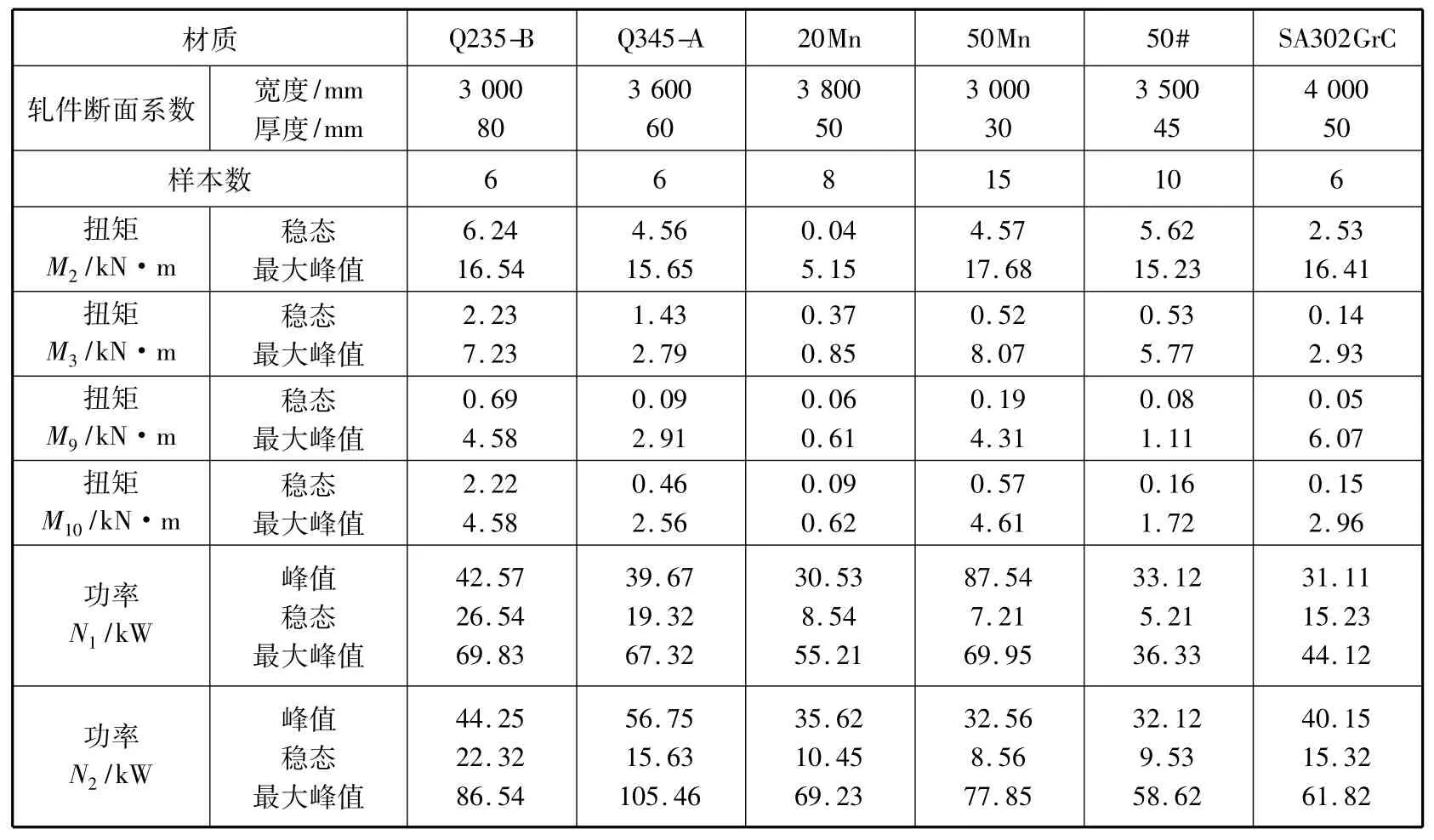
表1 各测点的扭矩及电机功率均值Table 1 The average value of torque moment and motor power on every measured point

3.4 矫直功率计算

当已确定矫直速度为ν，矫直机传动系统的效率为η 时，矫直机的驱动功率为

式中 M——作用在辊子上的总传动力矩，kN·m;

v——矫直速度，m/s;

D——矫直辊直径，m;

η——传动效率，一般取为0.7～0.9。

4 实验数据

本文实验用的矫直机为四重式全液压可逆十一辊式，主传动电机为两台AC690V，650 kW，1 000 r/min，矫直速度(0～±40～±60)m/min，最大矫直力30 000 kN。矫直辊的规格是∅285 mm×4 300 mm。轴承与机架为简支式结构。共采集了6 种不同钢种的信号。表1 列出不同材质的板材矫直时各接轴测点扭矩和两台电动机功率的记录数据。

5 结论与展望

(1)矫直机扭矩的计算是基于矫直过程中工件弯矩与曲率变化之间的关系计算得到的。

(2)新的矫直扭矩计算公式的计算结果基本与实验数据相符。

(3)被矫直工件的原始曲率对矫直扭矩的计算影响较大。如果可以找到一种方法确定工件原始曲率，将对矫直扭矩的计算产生深远的意义。

［1］王效岗.十五辊组合矫直机矫直模型研究［J］.四川大学学报(工程科学版)，2008，40(6)：181－185.

［2］张璇，王志刚，李友荣.基于辊间耦合的矫直机传动扭矩计算方法研究［J］.塑性工程学报，2009，16(5)：86－89.

［3］邹家祥.轧钢机械(3 版)［M］，北京：冶金工业出版社，2000：373－376.

［4］崔甫.矫直原理与矫直机械［M］，北京：冶金工业出版社，2002：178－184.

［5］黄庆学.轧钢机械设计［M］，北京：冶金工业出版社，2007：356－360.