基于强度折减法的边坡稳定性分析
李朝晖,陈建平,马艳玲
(1.江西铜业集团公司武山铜矿, 江西 九江市 332204;2.江西理工大学资源与环境工程学院, 江西赣州市 341000)
基于强度折减法的边坡稳定性分析
李朝晖1,陈建平2,马艳玲2
(1.江西铜业集团公司武山铜矿, 江西 九江市 332204;2.江西理工大学资源与环境工程学院, 江西赣州市 341000)
为了评价某山坡露天矿边坡的稳定性,应用有限差分强度折减法,对该矿山人工边坡的稳定性进行了计算分析,并与传统的极限平衡法的计算结果进行了对比。结果表明,由于有限差分强度折减法克服了极限平衡法未能考虑材料本构关系的不足,因而更能实际的模拟边坡计算模型,更客观的分析边坡的稳定状态,求得的边坡安全系数更为合理。
边坡稳定性;有限差分;强度折减法;安全系数
0 引言
某矿露天采场扩采范围地平标高为+103~+300 m,设计坑底最低标高为+103 m,上口封闭圈标高+135 m,最终设计边坡角54°,最终边坡高度190 m。在目前扩帮工程中,245 m平台以上揭露出软岩规模较大,延长2 km左右,走向东西,倾向北西转正北,倾角50°左右,该部分岩体极不稳定,有矽化破碎现象,虽然断层倾向和边坡倾向相反,但该部分岩体在雨水较多时遇水软化易失稳,造成上部260,285 m平台(已到设计最终边坡位置)边坡部分失稳滑坡,严重影响下部平台作业安全和开采进度。由于该边坡岩体工程地质特性复杂,在扩帮过程中存在滑坡、崩落等较为严重的地质灾害的可能性,对安全施工和生产带来了严重威胁。借助FLAC(有限差分法)软件,应用强度折减法对该矿山边坡的稳定性进行了计算和分析,并与极限平衡法的计算结果进行对比,评价及预测扩帮过程中永久边坡与过渡边坡可能发生的地质灾害,以指导现场施工。
1 FLAC强度折减法简介
三维快速拉格朗日法(FLAC)是一种基于三维显式有限差分方法的数值分析方法,其分析软件主要用于模拟岩土或其他材料的三维力学特性。
显式有限差分法的特点在于数值计算中无需像有限单元法一样将每个单元组装成庞大的总刚度矩阵,其计算速度快,存储量小,不存在计算收敛性问题。目前,在连续介质力学问题的范畴内,显式有限差分法已经被证明具有与有限元法同样准确的计算结果[1]。同时该方法能较好地模拟岩土材料在达到强度极限或屈服极限时发生塑性流动的力学行为,对比ANSYS等多场耦合有限元软件,FLAC更加适用于分析渐进破坏、失稳和模拟大变形问题,软件提供针对岩土体和支护体系的各种本构模型和结构单元,更突出了FLAC的“专业”特性,因此在国际岩体工程界非常流行[2]。
目前强度折减法已被证实是一种有效求解边坡稳定性系数的方法[3],且物理意义明确,即定义安全系数为岩土体的实际抗剪强度与与邻近破坏时的折减后剪切强度的比值。其基本原理是将岩土体强度指标c、φ值同时除以一个折减系数F:

然后再将折减后的c'、φ'值作为材料新的参数进行数值计算,不断的循环折减后,当边坡岩土体符合给定的临界破坏状态判定条件时,对应的F称为边坡的最小安全系数。
边坡稳定性作为岩土工程领域的一个热点研究课题,人们通常采用安全系数来评价其稳定性状态。因其原理简单同时物理意义明确,至今仍为边坡稳定性分析中最重要的指标之一。严格说来,安全系数是基于极限平衡法的一种评价指标,数值计算方法则是与极限平衡分析方法并行的一种分析方法,这两者本来是不存在交汇点,然而基于数值模拟技术的强度折减法的出现,改变了这一局面,强度折减法成为了联系着两种分析思想的纽带。
2 计算条件
2.1 计算模型
由于矿山为山坡露天开采,在采场走向上各岩层具有较好的一致性,本文以垂直采场走向的A—A剖面为例进行讨论分析。
露天边坡A—A剖面的模型网格见图1,边坡高度从300 m到103 m,最终边坡坡面角54°,一共划分14186个节点,13831个单元。
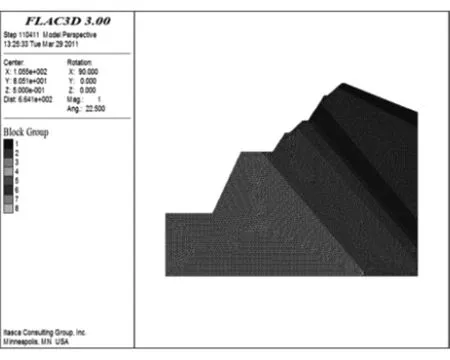
图1 模型网格
2.2 约束条件和初始条件
计算模型除顶部表面自由边界外,模型底部(z=0)设为固定约束边界,模型左侧施加水平方向位移约束,通过强度折减法寻找开挖后边坡的滑动面。在初始条件中,不考虑构造应力,仅考虑自重应力产生的初始应力场。
2.3 岩体力学参数
表1为参考岩石力学参数手册,采用内插法确定岩石力学参数,再折减得到岩体的强度参数。
在传统的极限平衡法中,简化毕肖普法(Bishop)是经典条分法的一种,它不仅考虑了土条侧面的作用力,同时假定各土条底部滑动面上的抗滑安全系数都是相同,整个滑动面的安全系数等于各土条底部滑动面的平均安全系数。简化毕肖普法将土坡稳定安全系数定义为沿整个滑裂面的抗剪强度与实际产生的剪应力之比,这使使得安全系数的物理意义明确,而且应用范围更加广泛,为非圆弧滑动分析及土条界面上条间力的各种考虑方式提供了有利条件[4,5]。本文选用简化毕肖普法对模型进行计算,将其结果和FLAC强度折减法进行比较。
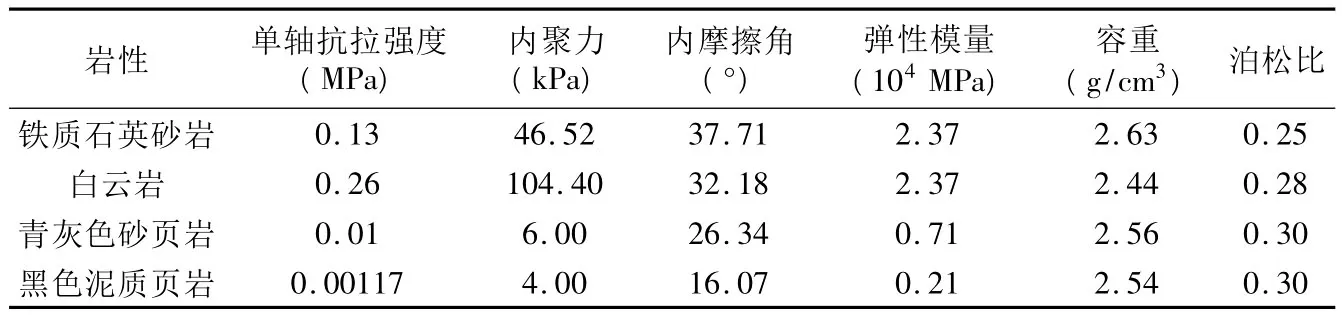
表1 岩石力学参数
3 计算结果与分析
用强度折减法算得A—A剖面的安全系数为0.52,一般来说,数值模拟安全系数在 1.2~1.3 以上为稳定状态的边坡,说明边坡整体开挖后处于稳定状态;再从剪应变增量位移矢量云图看,见图2,剪应变增量主要出现在245 m平台上部的260,285 m平台,产生滑移破坏,而不是整体的滑移破坏。

图2 A-A剖面强度折减后破坏时的剪应变增量和位移矢量云图
传统的极限平衡法中选用简化毕肖普法进行计算,计算出的安全系数Fs=0.5117,这和FLAC计算的结果十分接近;最危险滑面圆心坐标为(80.50,147.74),半径为 47.9 m,见图3。
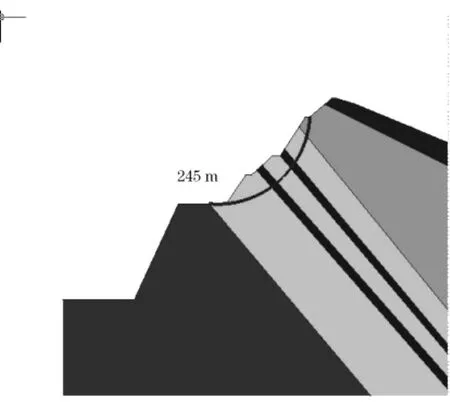
图3 简化毕肖普法自动搜索滑面位置
4 讨论
强度折减法和极限平衡法所计算出的边坡安全系数相差很小,且破坏面与搜索的最危险滑面非常相似,区别在于在FLAC强度折减法计算结果主要集中在245 m以上的260 m和285 m平台,而简化毕肖普法自动搜索滑面位置贯穿了265,275,280 m 3个平台。比较两者,FLAC强度折减法的计算结果和露天采场现状更加相符。另外,最为重要的是极限平衡法所能确定的破坏是开始时的,而FLAC不仅包含了应力重分布的影响,同时也反应了破坏发生之后的渐进发展。由于有限差分强度折减法能够克服极限平衡法未能考虑材料本构关系的不足,因而能够更加实际的模拟边坡稳定计算模型,能更加客观的分析出边坡的稳定状态,求得的边坡安全系数也更为合理。
[1] FLAC(Fast Lagraugian Analysis of Continua)User's Guide,Version 5.0[S].Itasca Consulting Group,Inc.,2005.
[2] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:水利水电出版社,2009.
[3] 郑颖人,陈祖煜,王恭先,等.边坡与滑坡工程治理[M].北京:人民交通出版社,2007.
[4] 陈祖煜,汪小刚,杨 健,等.岩质边坡稳定性分析—原理方法程序[M].北京:中国水利水电出版社,2005.
[5] 郑颖人,龚晓南.岩土塑性力学基础[M].北京:建筑工程出版社,1989.
2011-03-24)
李朝晖(1969-),男,江西铅山人,工程师,主要从事矿山工程技术的工作,Email:49137360@qq.com。
——读伊丽莎白·毕肖普《卡萨布昂卡》

