高速铁路桥隧沉降预测模型的研究

明祖涛，游振兴，张 届，阮汝伟

(中国地质大学(武汉)信息工程学院，湖北武汉430074)

高速铁路桥隧沉降预测模型的研究

明祖涛，游振兴，张 届，阮汝伟

(中国地质大学(武汉)信息工程学院，湖北武汉430074)

高速铁路线下桥梁、隧道结构不同，导致沉降规律差别很大，须分别进行研究。根据高速铁路桥隧沉降小量级、大波动的数据特点，对各种沉降预测方法进行系统研究，并结合实例，探索出与桥隧沉降相适应的高精度、高稳定性的预测方法，为今后高速铁路桥隧的沉降预测提供参考和借鉴。

高速铁路;沉降预测;三点法;GM(1，1)模型

一、引 言

目前，我国高速铁路的设计时速为 250～380 km/h，它具有高平顺、高稳定的特点。沉降变形预测方法中较为成熟的是基于实测的沉降-时间数据的推算法。具体可分为:属于静态预测的曲线拟合法，动态预测的灰色系统法、神经网络法。对于高速铁路小量级、大波动的沉降数据特点而言，缺乏相关经验。鉴于此，本文研究了基于实测的沉降-时间数据推算法的适用性。

二、高速铁路桥隧的特点与沉降预测方法分析

1.高速铁路桥隧的特点

桥梁是刚性构筑物，具有高稳定性的特征，而影响桥梁高平顺性的因素很多，除了预应力混凝土桥梁的徐变上拱、梁端转角和不均匀温差引起梁体结构变形外，还应考虑相邻桥梁墩台基础的不均匀沉降。

隧道是藏于山体的连续刚性构筑物，隧道内基底的稳定性是影响无碴轨道耐久性的重要因素。

2.沉降预测方法分析

目前，基于实测的沉降-时间数据的推算法，因其回避了理论计算的自身缺陷、计算参数值不准等因素，在各种工程中得到了广泛的应用。本文主要针对属于静态预测的规范双曲线、修正双曲线、三点法、Asaoka法和属于动态预测的GM(1，1)等模型进行对比分析，指出适于桥隧沉降预测的方法。

三、桥隧沉降预测模型对比分析

本文选取某高速铁路线下桥隧的观测数据作为分析对象，对常用的沉降预测方法进行对比分析研究。模型的精度采用曲线回归相关系数进行评定。

1.桥梁工程沉降预测模型对比分析

(1)桥梁沉降变形特征

桥梁地基处理方式一般为摩擦桩和柱桩，其表现形式为群桩，而群桩的基础沉降变形性状是桩-承台-地基土之间相互作用的综合影响结果，目前桥梁群桩基础沉降的计算只局限于瞬时和最终沉降两种情况，很少关注其沉降的时间效应。通过大量的桥梁墩台基础沉降观测资料积累发现，随着桥梁施工阶段的不同，其沉降-时间曲线变化存在一定的规律。高速铁路桥梁普遍采用预应力混凝土简支箱梁，其桥梁墩台基础的沉降变形特征表现为:随着桥梁墩台的浇筑，其沉降量随荷载的增加近线性增减;墩台施工完毕后至架梁期间，墩台的沉降随着简支箱梁荷载的一次施加，其曲线出现明显的拐点，沉降速率发生突变;架梁后一个月内，由架梁荷载引起的沉降增量逐渐变小;架梁后两个月以上，桥梁墩台基础沉降基本趋于稳定状态。

(2)预测模型对比分析

选取桥梁墩台的两个沉降变形观测点作为研究对象，墩台基础为摩擦桩，变形观测点里程为: DK0035+623、DK0039+487，对应的沉降-时间曲线趋如图1和图2所示。

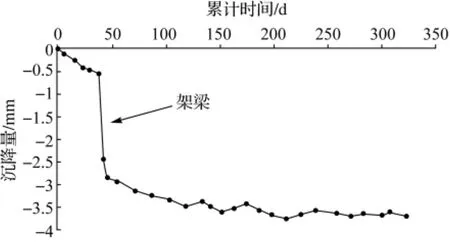
图1 DK0035+623观测点沉降-时间曲线

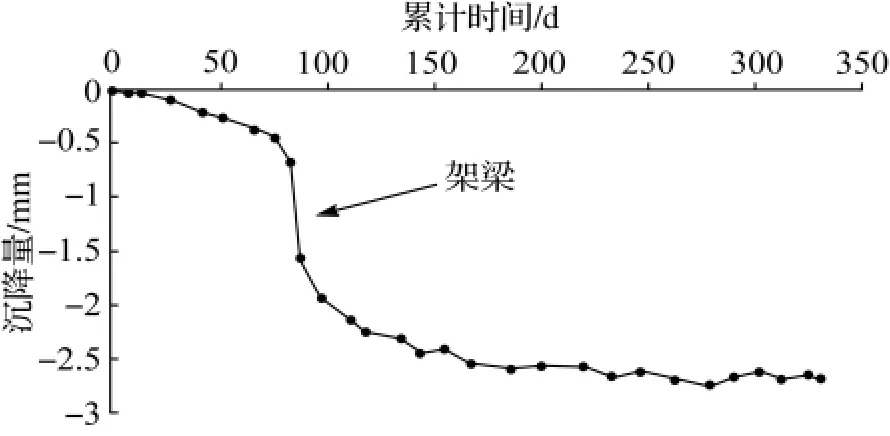
图2 DK0039+487观测点沉降-时间曲线

由图1、图2看出，架梁时由于荷载的一次性施加，桥墩基础在较短时间内出现较大的沉降，沉降-时间曲线图出现较大的拐点。架梁后桥梁处于恒载期，其沉降趋势发展比较平缓，在恒载3个月以后基本处于收敛状态。

在此采用规范双曲线、修正双曲线、三点法、Asaoka法和GM(1，1)模型对桥梁墩台基础沉降进行预测，其中规范双曲线只对恒载后数据进行预测，其他模型预测时间段为观测时间点到观测时间终点。各断面变形观测点预测残差对比图如图3、图4所示。

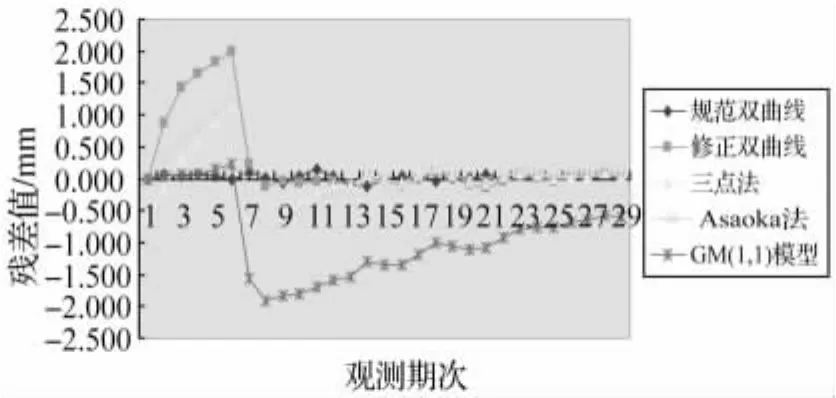
图3 DK0035+623观测点预测残差对比图

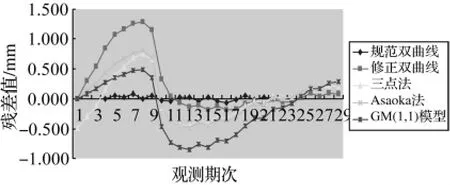
图4 DK0039+487观测点预测残差对比图

分析图3和图4得出，由于架梁前观测数据较少，数据平滑度较高，GM(1，1)模型对其预测误差较小;而规范双曲线法预测误差最大，主要原因是由于桥梁荷载变化不均匀造成的;三点法和Asaoka法预测误差在GM(1，1)模型和修正双曲线之间，总体上三点法预测情况好于Asaoka法。而对于架梁后的观测数据而言，由于架梁后桥梁处于恒载期间，沉降发展趋势不明显，数据的小波动对GM(1，1)模型预测精度产生较大的影响，预测误差较大，而其他模型预测误差基本处于同一级别上。为了进一步研究各模型在桥梁墩台沉降变形预测中的适用性，表1给出了各模型曲线回归相关系数。

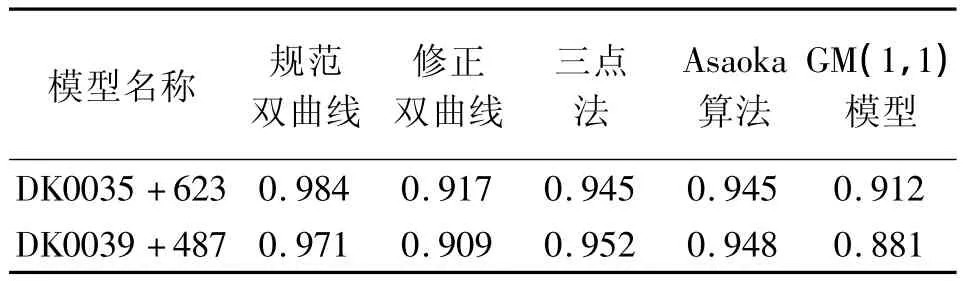
表1 曲线回归相关系数

通过表2比较各模型曲线回归相关系数，从总体上看，规范双曲线只采用恒载后的观测数据进行预测，避免了因架梁产生的曲线大波动的影响，其相关系数最高，满足大于0.92的要求;三点法采用恒载期的数据进行建模，在一定程度上避免了拐点对其预测的影响，其相关系数基本满足要求;Asaoka法相关系数基本满足大于0.92的要求;修正双曲线预测采用恒载前的大波动数据，其相关系数受数据波动的影响，相关系数很难满足规范要求;GM(1，1)模型对曲线平滑度要求很高，而架梁产生的数据大波动影响了模型的预测，其相关系数也很难满足要求。通过以上分析，对于代表观测断面，在桥梁墩台基础沉降曲线全程预测时，三点法和Asaoka法预测容易达到规范要求，修正双曲线和GM(1，1)模型容易受到数据大波动的影响，曲线回归相关系数很难达到要求。

由于桥梁基础沉降-时间曲线出现较大的拐点，为了更准确、更合理地预测桥梁基础沉降的趋势，应对桥梁基础沉降作两个阶段的曲线回归分析。根据沉降-时间曲线，以拐点为分界点，对桥梁作两个阶段的沉降预测分析:第一阶段对桥梁基础沉降作全程的预测分析，确定其沉降发展趋势;第二阶段对架梁后(恒载后)的观测数据作预测分析。综合两个阶段的预测结果来确定桥梁基础沉降的发展趋势。

研究得出，对于桥梁基础沉降的第一阶段预测中，因其沉降-时间曲线出现较大的拐点，GM(1，1)模型要求观测数据平滑度较高而不适用，修正双曲线因桥梁荷载的不均匀变化造成其曲线回归相关系数很难达到规范要求。三点法由于只采用了恒载期的观测数据进行预测，在一定程度上避免了拐点对曲线回归相关系数的影响，其曲线回归相关系数基本能满足规范要求，Asaoka算法的曲线回归相关系数基本能满足大于0.92的要求。因此，在桥梁沉降预测的第一阶段，首选三点法，其次为Asaoka算法。在桥梁沉降预测的第二阶段，即评测时间起点为恒载后，因其沉降发展趋势较为平缓，而数据波动较大，所以规范双曲线对此情况不适用。根据对路基的预测模型对比分析情况，预测时间起点对相关系数的影响规律，对桥梁的第二阶段的预测同样适用，因此，在桥梁的第二阶段的预测中，三点法作为优选预测方法，同时兼顾修正双曲线和Asaoka算法来修正。

2.隧道工程沉降预测模型对比分析

(1)隧道沉降变形特征

隧道开挖后，由于围岩应力得到释放，隧道底板基础岩体呈隆起趋势。随着隧道施工的进一步开展，隧道底板的回弹变形慢慢趋于稳定。当隧道施工进行到二次衬砌时，随着衬砌荷载的一次性施加，隧道线下结构开始沉降，达到一定时间后沉降趋于稳定。

(2)预测模型对比分析

选取某高速铁路一处隧道2个变形观测点作为研究对象，围岩级别均为V级，变形观测点的断面里程为:DK0034+568、DK0034+653，沉降变形观测点沉降-时间曲线如图5和图6所示。

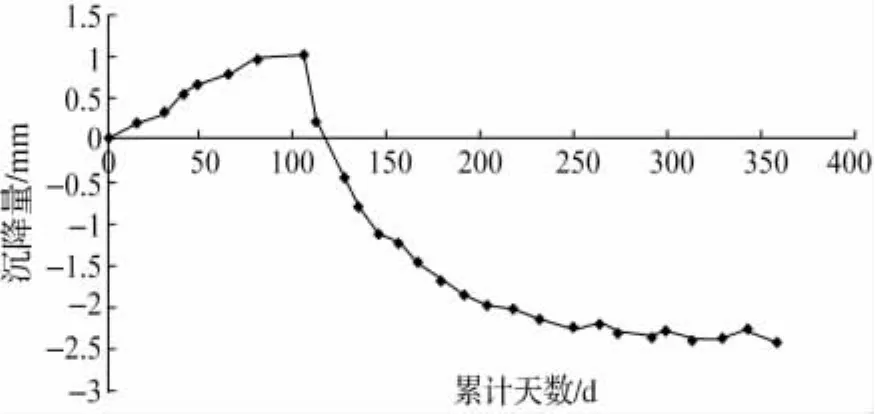
图5 DK0034+568(左)观测点沉降-时间曲线

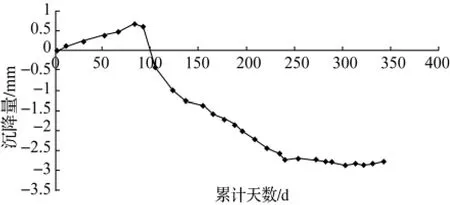
图6 DK0034+653(左)观测点沉降-时间曲线

结合图5、图6可以看出，观测点的沉降变形根据隧道施工阶段可划分为两个阶段:隧道二次衬砌前，线下结构产生弹性变形，沉降-时间曲线呈隆起状态;二次衬砌完成后，隧道线下结构开始下沉。因此，在进行预测时，需要指定预测的分界点，运用不同的预测方法分别对两段曲线进行拟合。此处选取的分界点为隧道线下结构开始下沉之日，各观测点预测残差对比如图7和图8所示。

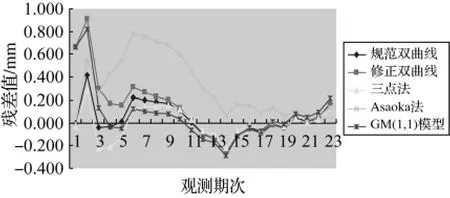
图7 DK0034+568(左)观测点预测残差对比图

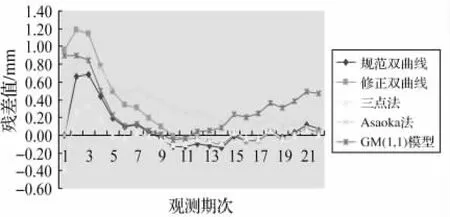
图8 DK0034+653(左)观测点预测残差对比图

综合分析图7和图8，从整体上看，三点法预测情况较好，预测误差较小，其次为修正双曲线，对后期数据预测精度与三点法处于同一级别，Asaoka法预测精度不稳定，主要是受到了预测计算前对原始数据的平滑处理的影响。同样，GM(1，1)模型受到了数据平滑度的影响，预测精度的稳定性较差。为了进一步研究各模型在隧道线下结构沉降变形预测中的适用性，表2给出了各模型的曲线回归相关系数。

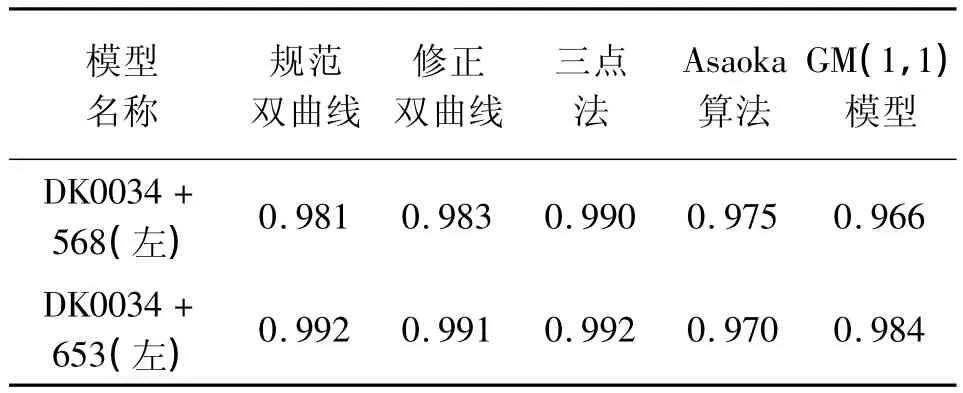
表2 曲线回归相关系数

从表2分析得出，对于选取的两个断面，三点法整体预测情况较好，预测精度的稳定性高，曲线回归相关系数较高;其次是修正双曲线，虽然其在负沉降数据期间预测误差偏大，但后续预测情况较好，曲线回归相关系数能满足要求;规范双曲线在数据较好的情况下预测良好，曲线回归相关系数也能达到规范要求。而Asaoka算法和GM(1，1)模型容易受到数据平滑度的影响，预测精度的稳定性欠佳，再次证明了此前的研究成果可靠。综合以上的研究得出:对于隧道第二阶段的沉降预测，本文首选三点法，修正双曲线作为次选方法;当三点法预测结果发生较大偏差时，用修正双曲线进行修正。

四、结束语

本文通过结合某高速铁路桥隧的沉降变形观测数据，分别用规范双曲线、修正双曲线、三点法、Asaoka法和GM(1，1)模型进行预测分析，研究各模型在桥隧沉降变形预测中的适用性、准确性和稳定性。最后得出:

1)对于桥梁而言，应对其分两个阶段进行沉降预测分析，在第一阶段，本文首选三点法，其次为Asaoka算法;在第二阶段，首选三点法，其次为修正双曲线。

2)对于隧道而言，根据隧道的沉降-时间曲线，同样应对隧道沉降分两个阶段进行，对于第二阶段的沉降预测，三点法能较好地反映其沉降发展趋势，相关系数较高作为首选方法，修正双曲线作为次选方法。

［1］ 尤昌龙.无碴轨道工后沉降变形观测、评估的集成理念［J］.铁道工程学报，2007(3):25-28.

［2］ 邓聚龙.灰色理论基础［M］.武汉:华中科技大学出版社，2002.

［3］ 李斌，朱健.非等间隔灰色GM(1，1)模型在沉降数据分析中的应用［J］.测绘科学，2003，32(4):50-55.

The Research of Settlement Prediction Model for the Bridge and Tunnel on High-speed Railway

MING Zutao，YOU Zhenxing，ZHANG Jie，RUAN Ruwei

0494-0911(2011)08-0017-03

TU196

B

2011-05-10

明祖涛(1969—)，男，湖北武汉人，副教授，主要从事精密工程测量与变形监测的教学与研究。