工程坐标与国家坐标转换参数选择与转换精度的关系研究
刘科利,姚吉利
(山东理工大学建筑工程学院,山东淄博255049)
工程坐标与国家坐标转换参数选择与转换精度的关系研究
刘科利,姚吉利
(山东理工大学建筑工程学院,山东淄博255049)
不同国家或地区在不同的历史时期采用的是不同的坐标系,因此存在着国家坐标和地方坐标之间的坐标转换。为了综合利用测绘成果,工程坐标与国家坐标进行相互转换是必要的。基于高斯平面的工程坐标与国家坐标转换模型,广泛采用相似变换。通过选择不同的相似变换参数,提出无需列误差方程和法方程即能得到转换参数最小二乘解的重心化模型,并推导出根据重心化参数计算有明确几何意义参数的公式。通过实例计算,证明该模型是正确、可靠的。
工程坐标;国家坐标;转换参数;形式参数;重心化
一、引 言
坐标转换分为二维坐标转换和三维坐标转换,由于一般工程的范围不大,经常采用二维坐标转换,也称为平面坐标转换。但有些现代大型工程规模有几十千米,甚至上百千米,起点至终点高差达几十米,甚至几百米,须选择具有高程抵偿面的任意带高斯投影平面直角坐标系统,仅进行二维坐标转换是不够的,必须进行三维坐标转换。文献[1]从极坐标和直角坐标的不同表达出发,导出了平面坐标的旋转转换,进而建立了平移、缩放、旋转同时作用的平面直角坐标转换和逆变换的模型。文献[2]通过两个坐标系坐标轴的几何关系,建立了平面坐标变换和逆变换的数学模型。文献[3]将罗德里格矩阵和反对称矩阵引入平面坐标转换模型,并将转换参数直接计算分为3步进行,且只用加减乘除计算转换矩阵,建立了两个坐标系统下坐标都有误差的平差模型,坐标转换理论比较完善,但存在如下问题:①以上文献都是建立在相似变换基础上进行的研究,部分参数的几何意义不明确,如文献[1-2]中的旋转角不明确;② 一套转换参数在使用上不方便,坐标转换是相互的,实用上最少应有两套转换参数,如计算出国家坐标转换到工程坐标的4个参数,还要计算出工程坐标转换到国家坐标的4个参数;③ 为了消除模型病态,解算的参数失去原来的几何意义,如文献[4]。本文针对上述3个问题,阐述了不同参数的几何意义,并推导出一套完整的参数关系公式,在实用上更加方便。
二、坐标转换模型及参数计算
1.坐标转换模型和参数几何意义
如图1所示,设某点国家坐标为(XP,YP),工程坐标为(xP,yP),则坐标转换模型为[1-3]

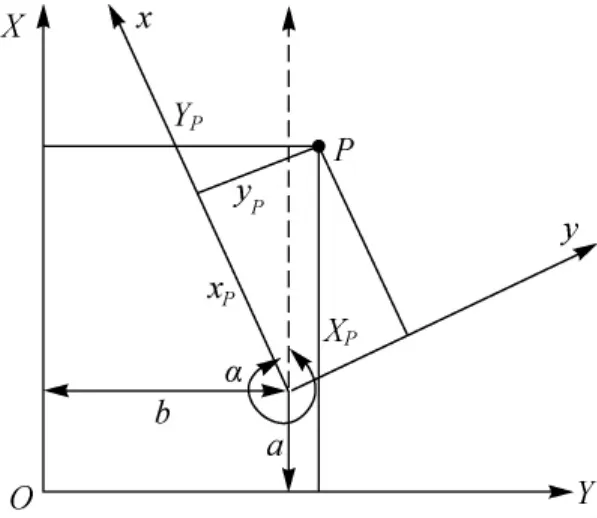
图1 坐标转换模型中各符号的意义
此式是非线性的,转换参数a、b称为平移参数,其几何意义是经过工程坐标系原点在国家坐标系的坐标;λ称为尺度参数,几何意义为相似比;α几何意义是工程坐标的x轴在国家坐标系的方位角。为了模型解算的方便,式(1)线性化形式可表示为
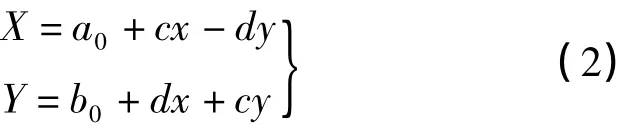
式中,a0、b0、c和d被称作形式参数,没有任何的几何意义,与转换参数的关系为

2.由两个公共点坐标计算转换参数
(1)按几何意义计算转换参数
先计算形式参数a0、b0、c和d。所谓公共点,就是两个坐标系均知道的点。按式(1)一个公共点可列2个方程,当两个坐标系有2对公共点时,4个参数便可唯一解出,根据平面转换的几何意义直接得到

(2)由形式参数计算转换参数
由式(2)得到2个公共点的方程
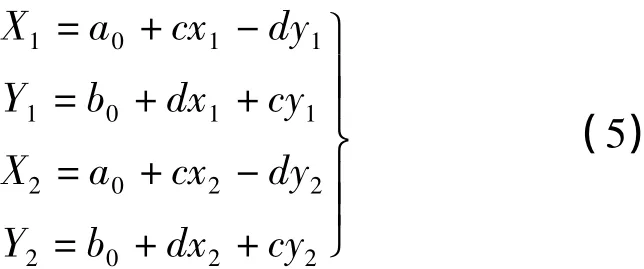
用式(5)中第3式减去第1式,第4式减去第2式,得

解出c、d

从而确定a0、b0

按式(3)解算出转换参数。
3.由国家坐标转换到工程坐标的4个参数的计算
由式(1)可得
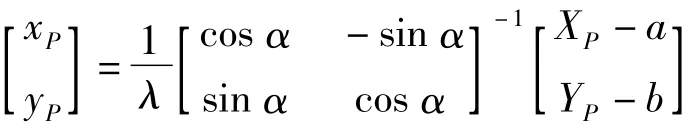
展开后

设由国家坐标转换到工程坐标的4个参数为u、v、m和β,标准形式为
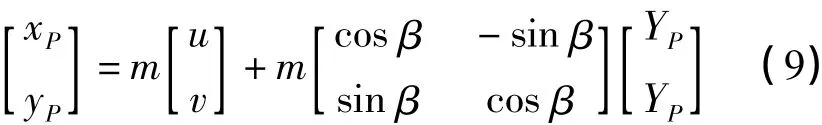
对照式(8)和式(9),国家坐标转换到工程坐标的4个参数u、v、m、β和a、b、λ、α的关系为
4.坐标转换平差模型中参数的计算
为了提高转换参数的精度和防止错误的发生,公共点的个数应多于2个,此时要进行最小二乘平差计算。因为式(1)不利于平差计算,所以选择线性化的式(2)进行平差计算,文献[4]给出了一种简便算法,可计算参数和对其精度进行评定,但按式(2)用原坐标建立的法方程是病态的,通常用重心化坐标计算[5],其步骤如下:
1)不列误差方程和法方程,只计算重心坐标之间的总和,即可直接计算形式参数。
2)计算转换参数。
3)精度检验。
所谓坐标重心化,就是把两个坐标系下的坐标平移到平差所用公共点平均坐标上的过程,重心化后形式参数的前两个为0,设重心化坐标为 ()和,重心坐标为(Xg,Yg)和(xg,yg),则

式中,n为参与平差公共点的个数,i=1,2,…,n;
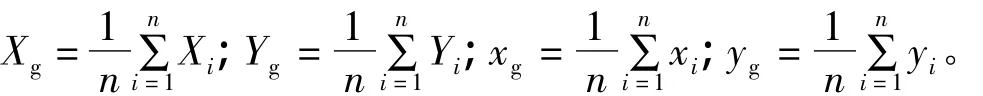
由式(2)得到的法方程为

解得

进而由式(3)算得λ、α。重心化下坐标转换关系为

将式(11)代入,得
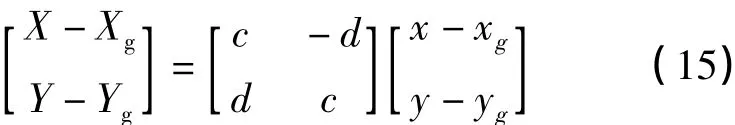
平移参数为

三、算例分析
笔者将本文所提出的简便算法应用于淄博市的工程坐标系与1980西安坐标系之间的转换,并进行了验证,取得了非常好的效果。该相互转换的坐标系有6个公共点,其坐标如表1所示,其中前4个点用于转换参数的计算,后两个点用于精度检验。

表1 1980西安坐标和工程坐标 m
按本文模型解算参数:a=-49.428 6,b=-4.164 9,λ=0.999 999 528 894 81,α=-2.570 7″用这4个参数计算得到的5点和6点的国家坐标见表2,差值见表2的6、7列,可见参数计算是正确的。

表2 计算坐标和原坐标比较m
四、结束语
本文系统阐述了工程坐标与国家坐标转换参数、形式参数及重心化参数之关系,并对转换参数的几何意义进行了图文解释。首次提出了不用列误差方程和法方程,就能得到转换参数的最小二乘解的重心化模型,并推导出根据重心化参数计算有明确几何意义的参数的公式。通过实例计算,说明本文模型是正确的,并且该模型简单明了,程序编写非常简单,计算量小,能在Excel表中实现所有计算。
[1] MOFFITT F H,MIKHAIL E M.Photogrammetry[M].New York:Happer&Row Publishers,1980:589-593.
[2] WOLF P R,GHILANI C D.Adjustment Computations[M].[S.l.]:John&Sons INC,1997:335-342.
[3] 姚吉利,王艳.基于罗德里格矩阵的平面坐标转换模型的建立[J].金属矿山,2005(11):40-42.
[4] 姚宜斌.平面坐标系统相互转换的一种简便算法[J].测绘信息与工程,2001(1):1-3.
[5] 李德仁.基础摄影测量学[M].北京:测绘出版社,1995.
On Relationship between Convertion Accuracy and Selection of Transformation Parameters of Engineering Coordinate and State Coordinate
LIU Keli,YAO Jili
0494-0911(2011)11-0050-03
P282.2
B
2010-11-15
刘科利(1966—),男,山东潍坊人,实验师,主要研究方向为测量数据处理。

