某些亚纯多叶函数的性质

邵礼翠, 朱 燕

(扬州大学 数学科学学院, 江苏 扬州 225002)

某些亚纯多叶函数的性质

邵礼翠, 朱 燕

(扬州大学 数学科学学院, 江苏 扬州 225002)

亚纯函数; 微分从属; Gauss超几何函数

0 引言

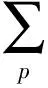
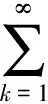
(1)

且在去心单位圆U*={z:z∈C,0lt;|z|lt;1}=U{0}内p叶解析的函数f(z)组成的函数类.

设f(z)和g(z)在U内解析,如果存在一个Schwarz函数w(z)在U内解析,并且w(0)=0,|w(z)|lt;1(z∈U),使得f(z)=g(w(z)),则称f(z)从属于g(z),记作fg.事实上,f(z)g(z)(z∈U)⟹f(0)=g(0),且f(U)⊂g(U).进一步,如果g(z)在U内单叶,则有f(z)g(z)(z∈U)⟺f(0)=g(0)且f(U)⊂g(U).

定义Gauss超几何函数2F1如下:

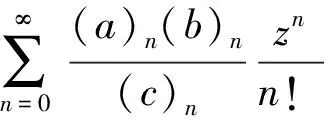
(2)

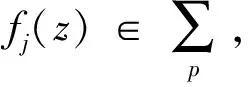
(3)

定义f1(z)和f2(z)的Hadamard卷积为

(4)

按照Pochhammer符号

(k)0=1,(k)n=k(k+1)(k+2)…(k+n-1)(n∈N),

定义函数:

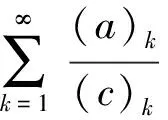
(5)

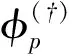
(6)

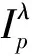
(7)

从(1)和(7)可看出,

(8)

由(8)容易看出

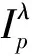
(9)

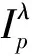
(10)

1 相关引理

引理1[7]设h在U内解析, 凸单叶,并且h(0)=1,

φ=1+b1z+b2z2+…,如果

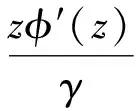
(11)

则φ(z)q(z)=γz-γtγ-1h(t)dth(z)(z∈U),并且q(z)是最佳控制.

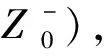
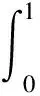
(12)

2F1(a,b;c;z)=2F1(b,a;c;z)

(13)

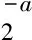
(14)

2 主要结果

若无特别说明,下文中agt;0,cgt;0,λgt;-p,-1≤Blt;A≤1.

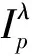
(15)

如果

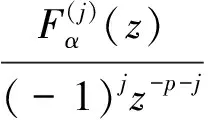
(16)

则

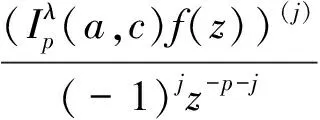
(17)

其中

证明由(14)和(9),可得

(18)

令

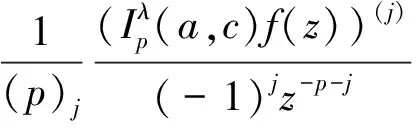
(19)

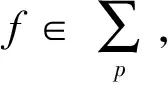
对(19)两边微分,可得

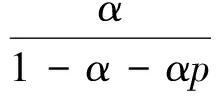
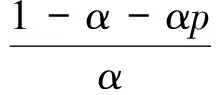
则

φ(z)q(z)

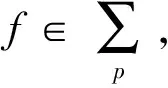
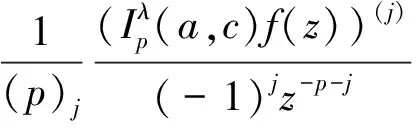
(20)

则

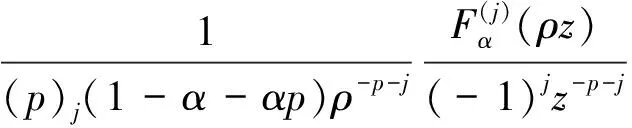
(21)

其中j∈N∪{0},αgt;0,

(22)

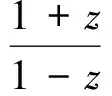
证明由定理1证明可知:

令

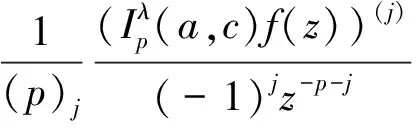
则φ(z)=1+b1z+b2z2+…

从(20)可得,

φ(z)h(z)(z∈U)

(23)

现在设

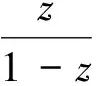
(24)

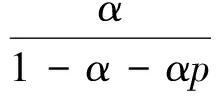
容易验证

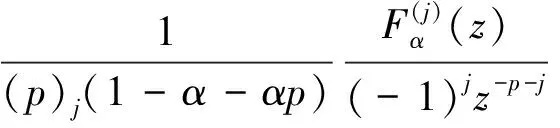
(25)

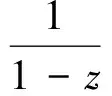
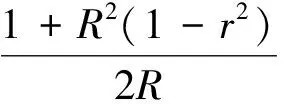
(26)

因此

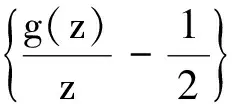
2(1-γ)Rcosθ+2γR2(2cos2θ-1)-1=R4γ(1-r2)2+R2[(1-γ)(1-r2)-2γr2]≥

R2[γ(1-r)2+(1-γ)(1-r2)-2γr2]=R2(1-2γr-r2)gt;0(|z|=rlt;ρ)，

所以

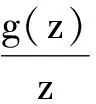
(27)

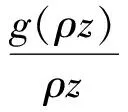
下证精确性.

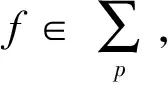
由于

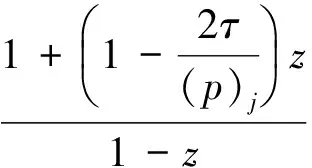
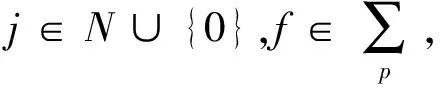
则

[1] Cho N E,Kwon O S, Srivastava H M. Inclusion relationships and argument properties for certain subclasses of multivalent functions associated with a family of linear operators?[J].Math Anal Appl, 2004, 292: 470-483.

[2] Liu J L, Patel J. Certain properties of multivalent functions associated with an extended fractionalDifferintegral operator?[J].Applied Mathematics and Computation, 2008, 203:703-713.

[3] Liu J L. Some properties of certain meromorphically multivalent functions?[J].Applied Mathematics and Computation, 2009, 210:136-140.

[4] Liu J L, Ahuja O P. Differential subordinations and argument inequalities?[J].Journal of the Franklin Institute, 2010, 347:1430-1436.

[5] Patel J, Cho N E, Srivastava H M.Certain subclasses of multivalent functions associated with a family of linear operators?[J].Mathematical and Computer Modelling, 2006, 43:320-338.

[6] Sokol J, Spelina L T. Convolutionproperties for certain classes of multivalent functions?[J].Math Anal Appl, 2008, 337:1190-1197.

[7] Miller S S, Mocanu P T. Differential subordinations and univalent functions?[J].Michigan Math, 1981, 28:157-171.

[8] Whittaker E T, Watson G N. A course on Modern Analysis:An Introduction to the General Theory of Infinite Processes and of Analytic Functions:with an Account of the Principle Transcendental Functions,fourthed?[M]. Cambridge University Press:Cambridge,1927.

[责任编辑：李春红]

SomePropertiesofCertainMeromorPhicallyMultivalentFunctions

SHAO Li-cui, ZHU-Yan

(Department of Mathematics, Yangzhou University, Yangzhou Jiangsu 225002， China)

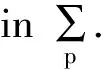
meromorphically functions; differential subordination; gauss hypergeometric function

O174.5

A

1671-6876(2011)02-0110-04

2010-12-25

邵礼翠(1984-), 女, 安徽怀远人, 硕士研究生, 研究方向为复分析.