带延迟修理的退化服务台排队系统更换模型研究*
贾积身,侯江华
(河南机电高等专科学校教务处,河南 新乡 453000)
1 引言
随着科学技术的发展和社会的进步,许多大中型企业的生产都采用了自动化生产线对产品进行连续生产,例如冶金轧钢系统等。这些自动化生产线在运行过程中,由于元部件的磨损和老化等原因常常会出现故障,如何对生产线进行维修与更换,实现最优控制已经成为一个重要的研究课题。
现有的排队论文献中所研究的系统几乎都是假定服务台(本文专指自动化生产线的核心部分)是不会失效的,可是在实践中,经常会遇到服务台发生故障而不能为顾客(本文专指自动化生产线正在生产的产品)服务的情形,此时需要修理工对服务台进行维修,修复后继续为顾客服务,对于这类服务可能失效和可修的排队系统,无论从排队论的角度,还是从可靠性理论的角度都是非常值得研究的,曹晋华和程侃[1]在假设服务台故障后能够得到及时维修和维修为“修复如新”的前提下,对M/G/1排队系统的排队论指标和可靠性指标进行了研究;钟福金[2]等研究了由一个自动轧钢电气设备组成的可修排队系统的最优更换模型,在假定该设备可修且不能“修复如新”的前提下,利用几何过程,研究了轧钢电气设备的更换策略,并且求出了系统期望费用的简明表达式;贾积身[3,4]在此基础上进一步假定服务台维修为“修复非新”的前提下,对服务台的更换策略进行了研究;Lam Yeh[5]等研究了可修服务台的M/M/1排队系统的几何过程模型,通过引入补充变量,得到了排队系统的一些性质和服务台的一些可靠性指标,并选择当服务台第N次故障时进行更换为更换策略进行了研究。然而,实际情况并非如此,在实际工程和生活中,服务台故障后往往得不到及时修理,系统故障后修理工首先是诊断故障原因或有的故障自己解决不了,还需要请其他修理工来进行修理,等等,这样就需要等待一段时间,不免引起服务台修理的延迟[6-8]。这种情形下服务台一般有三种状态:正常,待修,修理。所以,对这种情况进行研究是十分必要的,同时它也具有重要的理论意义和实用价值。
本文将在上述文献基础上提出一种新的更为一般的可修排队系统,即带修理延迟的服务台退化可修排队系统,并针对服务台每次维修后的修理时间随机递增、维修后的寿命随机递减的现实情况,利用几何过程,以被服务的顾客数N为其更换策略,选择最优的N*,使得服务台经长期运行单位时间内的期望效益达到最大,并求出了服务台经长期运行单位时间内期望效益的明显表达式。
为讨论方便,先给出随机序和几何过程的定义,详细内容可参见文献Lam Yeh[9]。
定义1 设ξ,η为两个随机变量,若对任意实数α,有
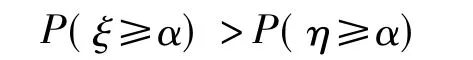
则称ξ随机地大于η,记为ξ>stη。同样,若ξ随机地小于η,记为ξ<stη。
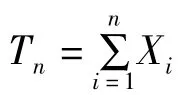

则称记数过程{ξ(t),t≥0}为一个几何过程。并称Tn为第n个变化时刻,Xn为第n个变化间距。显然
若α>1,{Xn,n=1,2,…}是随机递减的,相应的几何过程称为递减的几何过程;
若0<α<1,{Xn,n=1,2,…}是随机递增的,相应的几何过程称为递增的几何过程;
若α=1,{Xn,n=1,2,…}是独立同分布(分布函数为F(t))的随机变量序列,从而几何过程为更新过程。
2 模型假定
本文所讨论的策略都是在下述假定下进行的。
假定1 设服务台只有一个,且他只有忙期(指工作)和假期(指故障)两种状态。t=0时,服务台是新的,服务台更换时用同类型的更换,且更换时间忽略不计;
假定2 服务台故障时,有时不能立即被维修;A={服务台故障时能立即被维修},B={服务台故障时不能立即被维修},且p(A)=p;令Vn表示服务台在第n次故障的延迟修理时间,并假定{Vn,n=1,2,…}是独立同分布于分布函数H(t)(t≥0)的随机变量序列,且γ=EVn<+∞;
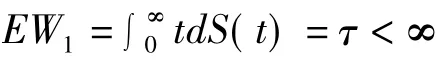
假定 4 Xn,Yn,Wn,Vn,n=1,2,…是相互独立;
假定5 服务台在单位时间内的维修费用为Cr,单位时间内的经济效益为Cω,服务台故障后延迟修理期间单位时间内的损失为C1,服务台一次更换费用为C。
3 策略N下的期望效益
设T1为服务台第一次更换时刻,Tn为服务台第n-1次与第n次更换之间的时间间隔,n=2,3,…,显然{Tn,n=1,2,…}形成一个更新过程。
设P(N)为在策略N下服务台经长期运行单位时间内的期望效益,则

由于{Tn,n=1,2,…}为一个更新过程,所以相邻两次更新时间间隔为更新周期长,由更新报酬定理得

设UN为服务台连续N个顾客服务结束的时刻,则他包括N个顾客的服务时间、服务台可能故障所需要的维修时间以及服务台故障所需要的待修时间。设K为服务台在连续N个顾客服务期内的故障次数,显然他是一个随机变量,由假定5知K=1,2,…。我们有

为了确定E(UN),需要先考虑随机变量K的分布律。


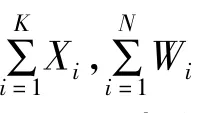
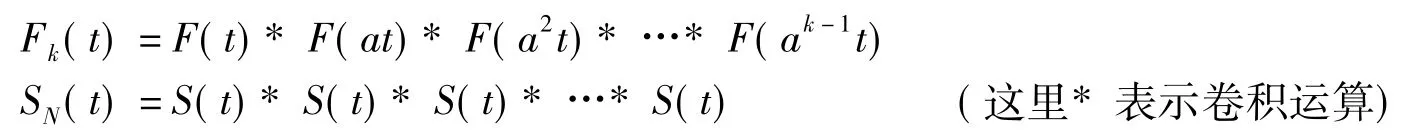
根据条件期望的性质和(2)式,得
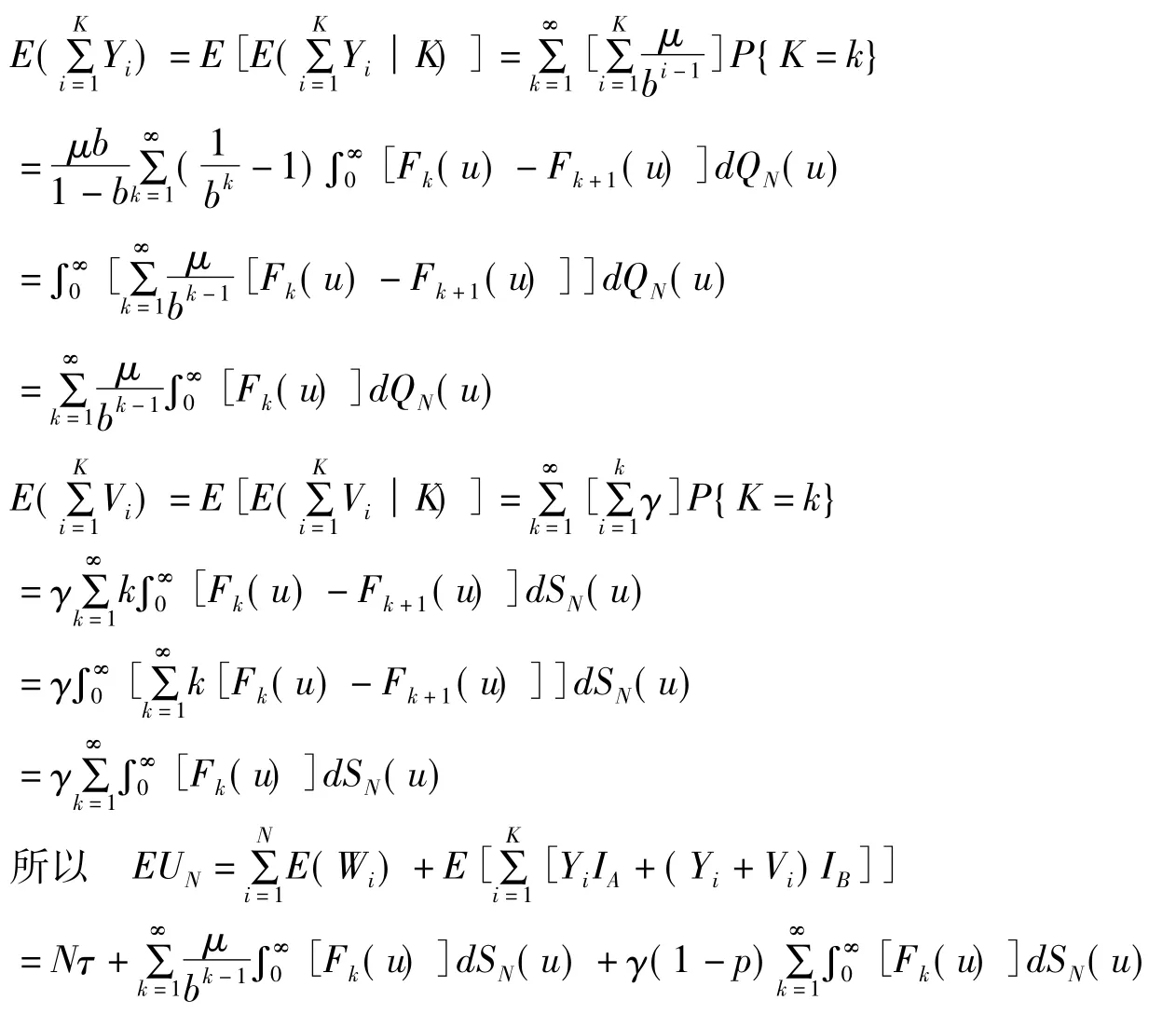
从而得到在策略N下服务台经长期运行单位时间内的期望效益为
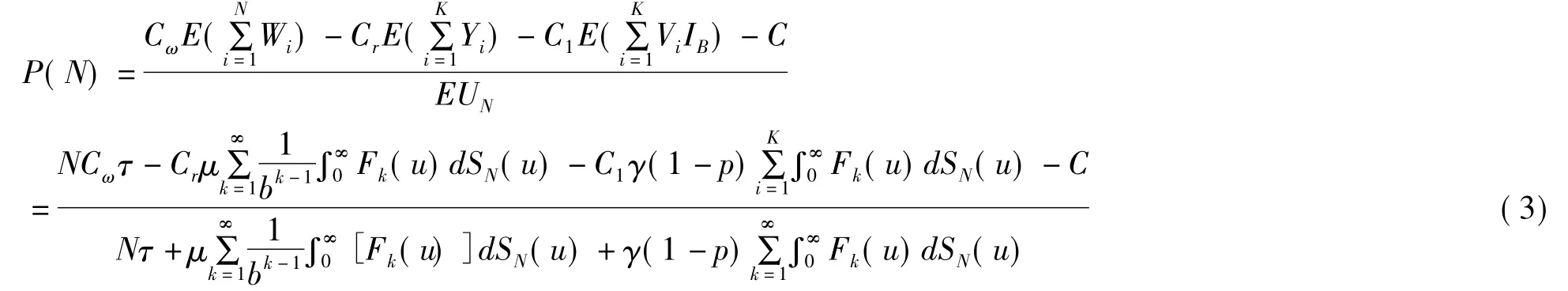
因此,要求P(N)的最大值,只需考虑下式的最大值即可。
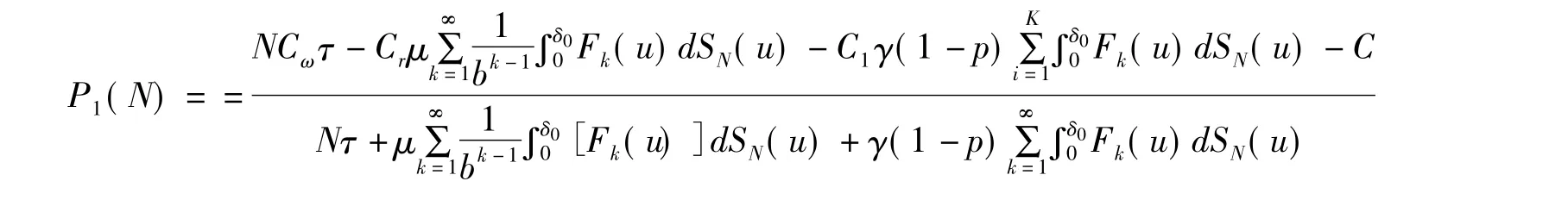
可通过数值法求出最优的策略N*,使得P1(N*)达到最大,也就是P(N*)达到最大。
4 讨论

(4)式表明服务台经长期运行单位时间内的最大期望效益为Cω。
2)若服务台能够“修复如新”,则a=b=1。这时(3)式变为
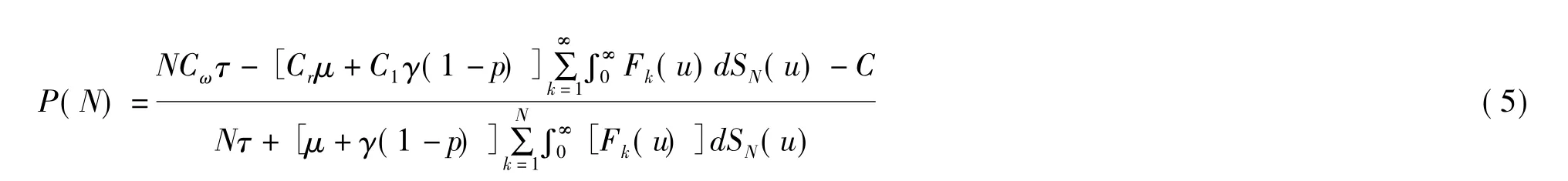
其中Fk(t)=F(t)*F(t)*F(t)*…*F(t),SN(t)=S(t)*S(t)*S(t)*…*S(t)
3)若服务台每次故障均能立即维修,则p=1。这时(3)式变为
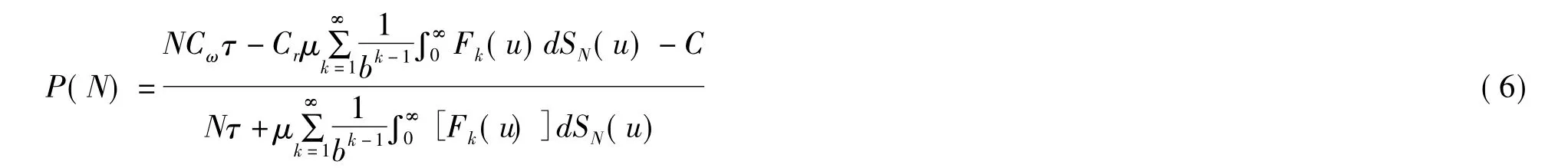
这正是文献[4]中的结论。
[1]曹晋华,程侃.服务台可修的M/G/1排队系统分析[J].应用数学学报,1982,5(2):113-127.
[2]钟福金,张元林,贾积身.自动化轧钢电气设备可修的排队系统的更换模型[J].东南大学学报,1994,24(6):89-92.
[3]贾积身.服务台“修复非新”的M/G/1排队系统更换模型研究[J].系统工程与电子技术,2003,25(12):254-256.
[4]Jia Jishen,Guo Baini.Optimal replacement policy for queueing system with repairable service station that repairing is not"as good as new"[J].Proceeding of the Jangjeon Mathematical Society,2003,6(1):65 -70.
[5]Lam Yeh,Zhang Yuan Lin,Qun Liu.A geometric process model for M/M/1 queueing system with a repairable service station[J].European Journal of Operations Research,2006,168:100 -121.
[6]毛勇,李才良,唐应辉.修理延迟的单部件系统的可靠性分析[J].电子科技大学学报,2000,29(5):545-548.
[7]Jia Jishen,Wu Shaomin,.A replacement policy for a repairable system with its repairman having multiple vacations[J].Computers & Industrial Engineering,2009,57(1):156 -160.
[8]贾积身,刘思峰,党耀国.延迟修理的修理工多重休假可修系统更换模型[J].系统工程与电子技术,2009,31(12):3017-3021.
[9]Lam Yeh.Geometric Processes and Replacement Problem[J].ACTA Mathematicae.Applicatae Sinica,1988,4(4):366-377 .

